Anova a due vie: definizione, formula ed esempio

Un’ANOVA a due vie (“analisi della varianza”) viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi indipendenti assegnati a due variabili (a volte chiamate “fattori”).

Questo tutorial spiega quanto segue:

• Quando utilizzare un’ANOVA bidirezionale.
• I presupposti che devono essere soddisfatti per eseguire un’ANOVA a due vie.
• Un esempio di come eseguire un’ANOVA bidirezionale.

Quando utilizzare un’ANOVA bidirezionale

È necessario utilizzare un’ANOVA bidirezionale quando si desidera sapere in che modo due fattori influenzano una variabile di risposta e se esiste o meno un effetto di interazione tra i due fattori sulla variabile di risposta.

Supponiamo, ad esempio, che un botanico voglia esplorare il modo in cui l’esposizione al sole e la frequenza dell’irrigazione influiscono sulla crescita delle piante. Pianta 40 semi e li lascia crescere per due mesi in diverse condizioni di esposizione al sole e frequenza di irrigazione. Dopo due mesi registra l’altezza di ogni pianta.

In questo caso abbiamo le seguenti variabili:

• Variabile di risposta: crescita delle piante
• Fattori: esposizione al sole, frequenza di irrigazione

E vorremmo rispondere alle seguenti domande:

• L’esposizione al sole influisce sulla crescita delle piante?
• La frequenza dell’irrigazione influisce sulla crescita delle piante?
• Esiste un effetto di interazione tra l’esposizione al sole e la frequenza di irrigazione? (ad esempio, l’effetto dell’esposizione al sole sulle piante dipende dalla frequenza di irrigazione)

Utilizzeremmo un’ANOVA a due vie per questa analisi perché abbiamo due fattori. Se, invece, volessimo sapere in che misura la sola frequenza di irrigazione influisce sulla crescita delle piante, utilizzeremmo un’ANOVA unidirezionale poiché lavoreremo con un solo fattore.

Ipotesi di ANOVA bidirezionale

Affinché i risultati di un’ANOVA a due vie siano validi, devono essere soddisfatte le seguenti ipotesi:

1. Normalità – La variabile di risposta è distribuita approssimativamente normalmente per ciascun gruppo.

2. Variazioni uguali – Le varianze per ciascun gruppo dovrebbero essere approssimativamente uguali.

3. Indipendenza – Le osservazioni all’interno di ciascun gruppo sono indipendenti l’una dall’altra e le osservazioni all’interno dei gruppi sono state ottenute mediante campionamento casuale.

ANOVA bidirezionale: esempio

Un botanico vuole sapere se la crescita delle piante è influenzata dall’esposizione alla luce solare e dalla frequenza delle annaffiature. Pianta 40 semi e li lascia crescere per due mesi in diverse condizioni di esposizione al sole e frequenza di irrigazione. Dopo due mesi registra l’altezza di ogni pianta. I risultati sono mostrati sotto:

Nella tabella sopra vediamo che sono state coltivate cinque piante in ciascuna combinazione di condizioni.

Ad esempio, cinque piante sono state coltivate con irrigazione quotidiana e senza luce solare e la loro altezza dopo due mesi era di 4,8 pollici, 4,4 pollici, 3,2 pollici, 3,9 pollici e 4,4 pollici:

Esegue un’ANOVA bidirezionale in Excel e ottiene il seguente risultato:

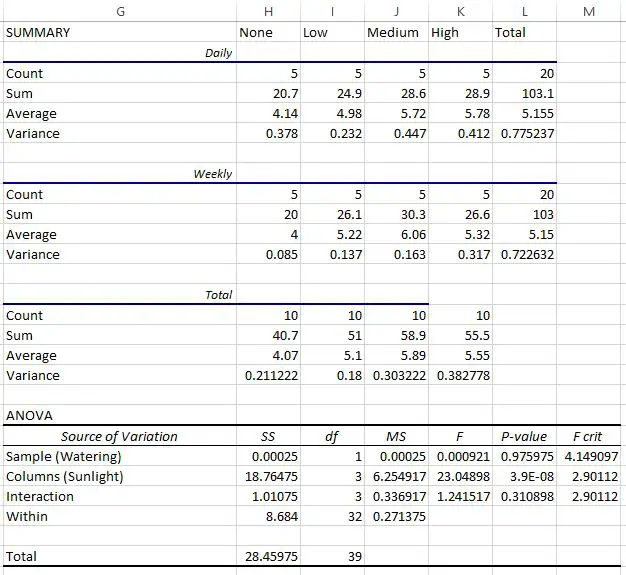
L’ultima tabella mostra il risultato dell’ANOVA a due vie. Possiamo osservare quanto segue:

• Il valore p per l’interazione tra la frequenza di irrigazione e l’esposizione al sole era 0,310898 . Ciò non è statisticamente significativo al livello alfa 0,05.
• Il valore p per la frequenza di irrigazione era 0,975975 . Ciò non è statisticamente significativo al livello alfa 0,05.
• Il valore p per l’esposizione al sole era 3,9E-8 (0,000000039) . Ciò è statisticamente significativo al livello alfa di 0,05.

Questi risultati indicano che l’esposizione al sole è l’unico fattore con un effetto statisticamente significativo sull’altezza delle piante.

E poiché non vi è alcun effetto di interazione, l’effetto dell’esposizione al sole è coerente a ciascun livello di frequenza di irrigazione.

In poche parole, il fatto che una pianta venga annaffiata quotidianamente o settimanalmente non ha alcun impatto sul modo in cui l’esposizione al sole influisce sulla pianta.

Risorse addizionali

I seguenti articoli spiegano come eseguire un’ANOVA bidirezionale utilizzando diversi software statistici:

Come eseguire un’ANOVA bidirezionale in Excel
Come eseguire l’ANOVA bidirezionale in R
Come eseguire un’ANOVA bidirezionale in Python
Come eseguire un’ANOVA bidirezionale in SPSS
Come eseguire un’ANOVA bidirezionale in Stata