Come eseguire manualmente un'anova bidirezionale

Un’ANOVA a due vie viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi indipendenti che sono stati suddivisi in due fattori.

Questo tutorial spiega come eseguire manualmente un’ANOVA bidirezionale.

Esempio: ANOVA bidirezionale manuale

Supponiamo che un botanico voglia sapere se la crescita delle piante è influenzata dall’esposizione alla luce solare e dalla frequenza dell’irrigazione. Pianta 40 semi e li lascia crescere per un mese in diverse condizioni di esposizione al sole e frequenza di irrigazione.

Dopo un mese, registra l’altezza di ciascuna pianta. I risultati sono mostrati sotto:

Nella tabella sopra vediamo che sono state coltivate cinque piante in ciascuna combinazione di condizioni.

Ad esempio, cinque piante sono state coltivate con irrigazione quotidiana e senza luce solare e la loro altezza dopo due mesi era di 4,8 pollici, 4,4 pollici, 3,2 pollici, 3,9 pollici e 4,4 pollici:

Possiamo utilizzare i seguenti passaggi per eseguire un’ANOVA bidirezionale:

Passaggio 1: calcolare la somma dei quadrati per il primo fattore (frequenza di irrigazione)

Per prima cosa calcoleremo l’altezza media complessiva delle 40 piante:

Media complessiva = (4,8 + 5 + 6,4 + 6,3 + … + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525

Successivamente, calcoleremo l’altezza media di tutte le piante annaffiate quotidianamente:

Media giornaliera = (4,8 + 5 + 6,4 + 6,3 + … + 4,4 + 4,8 + 5,8 + 5,8) /20 = 5,155

Successivamente, calcoleremo l’altezza media di tutte le piante innaffiate ogni settimana:

Media settimanale = (4,4 + 4,9 + 5,8 + 6 + … + 3,9 + 4,8 + 5,5 + 5,5) /20 = 5,15

Successivamente, calcoleremo la somma dei quadrati per il fattore “frequenza di irrigazione” utilizzando la seguente formula:

Σn(X _j – X ..) ²

Oro:

• n : la dimensione del campione del gruppo j
• Σ : simbolo greco che significa “somma”
• X _j : la media del gruppo j
• X .. : la grande media

Nel nostro esempio, calcoliamo la somma dei quadrati per il fattore “frequenza di irrigazione” come segue: 20(5,155-5,1525) ² + 20(5,15-5,1525) ² = 0,00025

Passaggio 2: calcolare la somma dei quadrati per il secondo fattore (esposizione al sole)

Per prima cosa calcoleremo l’altezza media complessiva delle 40 piante:

Media complessiva = (4,8 + 5 + 6,4 + 6,3 + … + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525

Successivamente, calcoleremo l’altezza media di tutte le piante non esposte al sole:

Media senza sole = (4,8 + 4,4 + 3,2 + 3,9 + 4,4 + 4,4 + 4,2 + 3,8 + 3,7 + 3,9) / 10 = 4,07

Ripeteremo questo calcolo per trovare l’altezza media delle piante sottoposte a diverse esposizioni solari:

• Media di soleggiamento basso = 5,1
• Luce solare media media = 5,89
• Soleggiamento medio elevato = 5,55

Successivamente, calcoleremo la somma dei quadrati per il fattore “esposizione al sole” utilizzando la seguente formula:

Σn(X _j – X ..) ²

Oro:

• n : la dimensione del campione del gruppo j
• Σ : simbolo greco che significa “somma”
• X _j : la media del gruppo j
• X .. : la grande media

Nel nostro esempio, calcoliamo la somma dei quadrati per il fattore “esposizione al sole” come segue: 10(4.07-5.1525) ² + 10(5.1-5.1525) ² + 10(5.89 -5.1525) ² + 10(5.55-5.1525) ² = 18,76475

Passaggio 3: calcolare la somma dei quadrati all’interno (errore)

Successivamente, calcoleremo la somma dei quadrati prendendo la somma dei quadrati delle differenze tra ciascuna combinazione di fattori e le altezze delle singole piante.

Ad esempio, l’altezza media di tutte le piante annaffiate quotidianamente senza esposizione alla luce solare è 4,14. Possiamo quindi calcolare la somma dei quadrati delle differenze per ciascuna di queste singole piante come segue:

• SS per irrigazione giornaliera e senza sole: (4.8-4.14) ² + (4.4-4.14) ² + (3.2-4.14) ² + (3.9-4.14) ² + (4.4-4.14) ² = 1.512

Possiamo ripetere questo processo per ogni combinazione di fattori:

• SS per irrigazione quotidiana e scarsa luce solare: 0,928
• SS per irrigazione giornaliera e soleggiamento medio: 1.788
• SS per irrigazione quotidiana e forte luce solare: 1.648
• SS per irrigazione settimanale senza sole: 0,34
• SS per irrigazione settimanale e scarsa luce solare: 0,548
• SS per irrigazione settimanale e soleggiamento medio: 0,652
• SS per irrigazione settimanale e forte luce solare: 1.268

Possiamo quindi sommare tutti questi valori per trovare la somma dei quadrati interni (errore):

Somme dei quadrati entro = 1,512 + 0,928 + 1,788 + 1,648 + 0,34 + 0,548 + 0,652 + 1,268 = 8,684

Passaggio 4: Calcola la somma totale dei quadrati

Quindi possiamo calcolare la somma totale dei quadrati prendendo la somma delle differenze tra l’altezza di ciascuna pianta e la media generale:

Somma totale dei quadrati = (4,8 – 5,1525) ² + (5 – 5,1525) ² + … + (5,5 – 5,1525) ² = 28,45975

Passaggio 5: calcolare la somma dell’interazione dei quadrati

Successivamente, calcoleremo l’interazione della somma dei quadrati utilizzando la seguente formula:

• Interazione SS = Totale SS – Fattore SS 1 – Fattore SS 2 – Interno SS
• Interazione SS = 28,45975 – 0,00025 – 18,76475 – 8,684
• Interazione SS = 1.01075

Passaggio 6: completare la tabella ANOVA

Infine, inseriremo i valori della tabella ANOVA a due vie:

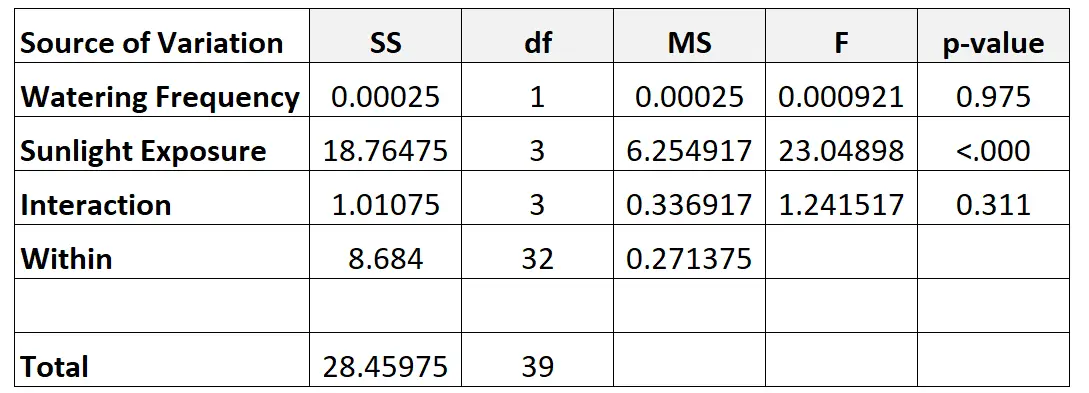
Ecco come abbiamo calcolato i diversi numeri nella tabella:

• df Frequenza di irrigazione: d-1 = 2-1 = 1
• df Esposizione al sole: k-1 = 4-1 = 3
• dfInterazione : (j-1)*(k-1) = 1*3 = 3
• df In : n – (j*k) = 40 – (2*4) = 32
• df totale: n-1 = 40-1 = 39
• MS: SS/DF
• Frequenza di irrigazione F : frequenza di irrigazione MS/MS interna
• F Esposizione alla luce solare : esposizione MS / MS alla luce solare in ambienti chiusi
• Interazione F : Interazione MS / MS Within
• Frequenza di irrigazione del valore p : il valore p che corrisponde al valore F di 0,000921 con il numeratore df = 1 e il denominatore df = 32
• Valore p dell’esposizione solare : il valore p che corrisponde al valore F di 23.04898 con il numeratore df = 3 e il denominatore df = 32
• Interazione del valore p : il valore p che corrisponde al valore F di 1.241517 con il numeratore df = 3 e il denominatore df = 32

Nota n.1: n = numero totale di osservazioni, j = numero di livelli per la frequenza di irrigazione, k = numero di livelli per l’esposizione al sole.

Nota n.2 : i valori p che corrispondono al valore F sono stati calcolati utilizzando il calcolatore della distribuzione F.

Passaggio 7: interpretare i risultati

Dalla tabella ANOVA possiamo osservare quanto segue:

• Il valore p per l’interazione tra la frequenza di irrigazione e l’esposizione al sole era 0,311 . Questo non è statisticamente significativo con α = 0,05.
• Il valore p per la frequenza di irrigazione era 0,975 . Questo non è statisticamente significativo con α = 0,05.
• Il valore p per l’esposizione al sole era <0,000 . Ciò è statisticamente significativo con α = 0,05.

Questi risultati indicano che l’esposizione al sole è l’unico fattore con un effetto statisticamente significativo sull’altezza delle piante.

E poiché non vi è alcun effetto di interazione, l’effetto dell’esposizione al sole è coerente a ciascun livello di frequenza di irrigazione.

In poche parole, il fatto che una pianta venga annaffiata quotidianamente o settimanalmente non ha alcun impatto sul modo in cui l’esposizione al sole influisce sulla pianta.

Risorse addizionali

Le seguenti esercitazioni forniscono informazioni aggiuntive sulle ANOVA:

Come eseguire manualmente un’ANOVA unidirezionale
Come eseguire manualmente un’ANOVA di misure ripetute
La guida completa: come riportare i risultati ANOVA bidirezionali