Come eseguire manualmente un'anova di misure ripetute
Un’ANOVA a misure ripetute viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi in cui compaiono gli stessi soggetti in ciascun gruppo.
Questo tutorial spiega come eseguire manualmente un’ANOVA a misure ripetute unidirezionali.
Esempio: misure ripetute unidirezionali ANOVA manualmente
I ricercatori vogliono sapere se tre diversi farmaci causano tempi di reazione diversi. Per testarlo, misurano il tempo di reazione (in secondi) di cinque pazienti a ciascun farmaco. I risultati sono mostrati sotto:
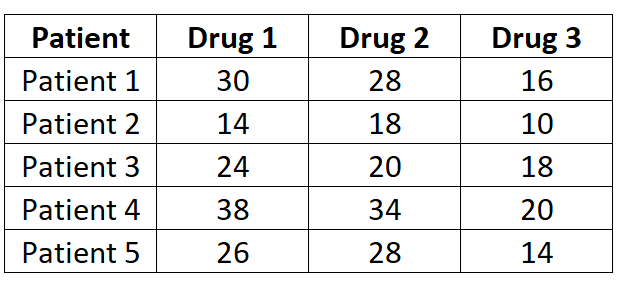
Poiché ogni paziente viene misurato con ciascuno dei tre farmaci, utilizzeremo un’ANOVA a misure ripetute unidirezionali per determinare se il tempo di reazione medio differisce tra i farmaci.
Seguire i seguenti passaggi per eseguire manualmente l’ANOVA a misure ripetute:
Passaggio 1: calcolare l’SST.
Per prima cosa calcoleremo la somma totale dei quadrati (SST), che può essere trovata utilizzando la seguente formula:
SST = s 2 totale (n totale -1)
Oro:
- s 2 totale : la varianza per il set di dati
- n totale : il numero totale di osservazioni nel set di dati
In questo esempio, calcoliamo l’SST come segue: (64.2667)(15-1) = 899.7
Passaggio 2: calcolare SSB
Successivamente, calcoleremo la somma dei quadrati (SSB), che può essere trovata utilizzando la seguente formula:
SSB = Σn j ( x j – x totale ) 2
Oro:
- Σ : simbolo greco che significa “somma”
- n j : il numero totale di osservazioni nel jesimo gruppo
- x j : la media del jesimo gruppo
- x totale : la media di tutti i dati
In questo esempio, calcoliamo SSB come segue: (5)(26,4-22,533) 2 +(5)(25,6-22,533) 2 + (5)(15,6-22,533) 2 = 362,1
Passaggio 3: calcolare l’SSS.
Successivamente, calcoleremo la somma dei quadrati in oggetto (SSS), che può essere trovata utilizzando la seguente formula:
SSS =( Σr2k /c) – ( N2 /rc)
Oro:
- Σ : simbolo greco che significa “somma”
- r 2 k : somma quadrata del k-esimo paziente
- N: il totale complessivo di tutti i dati
- r: numero totale di pazienti
- c: numero totale di gruppi
In questo esempio, calcoliamo SSS come segue: ((74 2 + 42 2 + 62 2 + 92 2 + 68 2 )/3) – (338 2 /(5)(3)) = 441,1
Passaggio 4: calcolare il SES.
Successivamente, calcoleremo la somma dell’errore quadrato (SSE), che può essere trovato utilizzando la seguente formula:
SSE = SST – SSB – SSS
In questo esempio, calcoliamo il SES come segue: 899,7 – 362,1 – 441,1 = 96,5
Passaggio 5: completare la tabella ANOVA delle misure ripetute.
Ora che abbiamo SSB, SSS e SSE, possiamo popolare la tabella ANOVA delle misure ripetute:
| Fonte | Somma dei quadrati (SS) | df | Quadrati medi (MS) | F |
|---|---|---|---|---|
| Fra | 362.1 | 2 | 181.1 | 15.006 |
| Soggetto | 441.1 | 4 | 110.3 | |
| Errore | 96,5 | 8 | 12.1 |
Ecco come abbiamo calcolato i diversi numeri nella tabella:
- df tra: #gruppi – 1 = 3 – 1 = 2
- df oggetto: #partecipanti – 1 = 5 – 1 = 4
- Errore df: df tra * df soggetto = 2*4 = 8
- Entra MS: Entra SSB / df = 362,1 / 2 = 181,1
- Materia MS: Materia SSS / df = 441,1 / 4 = 110,3
- Errore MS: errore SSE / df = 96,5 / 8 = 12,1
- F: MS entra / errore MS = 181.1 / 12.1 = 15.006
Passaggio 6: interpretare i risultati.
La statistica del test F per questa ANOVA a misure ripetute unidirezionali è 15.006 . Per determinare se si tratta di un risultato statisticamente significativo, dobbiamo confrontarlo con il valore F critico trovato nella tabella di distribuzione F con i seguenti valori:
- α (livello di significatività) = 0,05
- DF1 (gradi di libertà del numeratore) = df tra = 2
- DF2 (gradi di libertà del denominatore) = errore df = 8
Troviamo che il valore critico di F è 4.459 .
Poiché la statistica del test F nella tabella ANOVA è maggiore del valore critico F nella tabella di distribuzione F, rifiutiamo l’ipotesi nulla. Ciò significa che abbiamo prove sufficienti per affermare che esiste una differenza statisticamente significativa tra i tempi di risposta medi dei farmaci.