Anova a una via: definizione, formula ed esempio
Un’ANOVA unidirezionale (“analisi della varianza”) confronta le medie di tre o più gruppi indipendenti per determinare se esiste una differenza statisticamente significativa tra le medie della popolazione corrispondente.
Questo tutorial spiega quanto segue:
- La motivazione per eseguire un’ANOVA unidirezionale.
- Le ipotesi che devono essere soddisfatte per eseguire un’ANOVA unidirezionale.
- Il processo per eseguire un’ANOVA unidirezionale.
- Un esempio di come eseguire un’ANOVA unidirezionale.
ANOVA unidirezionale: motivazione
Supponiamo di voler sapere se tre diversi programmi di preparazione ai test portano o meno a punteggi medi diversi in un esame di ammissione all’università. Dato che ci sono milioni di studenti delle scuole superiori in tutto il paese, sarebbe troppo dispendioso in termini di tempo e denaro rivolgersi a ogni studente e consentire loro di utilizzare uno dei programmi di preparazione ai test.
Invece, potremmo selezionare tre campioni casuali di 100 studenti dalla popolazione e consentire a ciascun campione di utilizzare uno dei tre programmi di preparazione ai test per prepararsi all’esame. Quindi potremmo registrare i punteggi di ogni studente una volta sostenuto l’esame.
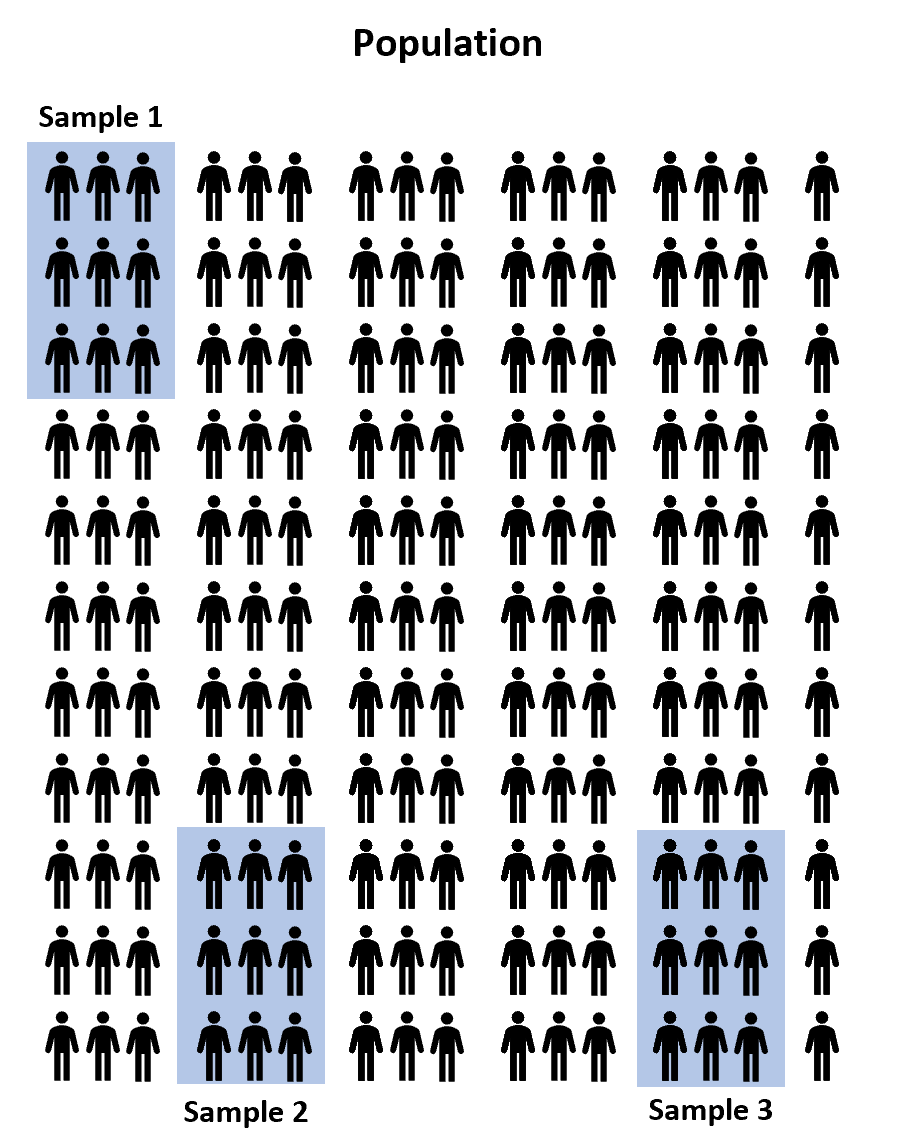
Tuttavia, è praticamente garantito che il punteggio medio dell’esame tra i tre campioni sarà almeno leggermente diverso. La questione è se questa differenza sia statisticamente significativa . Fortunatamente, un’ANOVA unidirezionale ci consente di rispondere a questa domanda.
ANOVA unidirezionale: ipotesi
Affinché i risultati di un’ANOVA unidirezionale siano validi, devono essere soddisfatte le seguenti ipotesi:
1. Normalità – Ogni campione è stato estratto da una popolazione distribuita normalmente.
2. Varianze uguali – Le varianze delle popolazioni da cui vengono estratti i campioni sono uguali. Puoi utilizzare il test di Bartlett per verificare questa ipotesi.
3. Indipendenza – Le osservazioni all’interno di ciascun gruppo sono indipendenti l’una dall’altra e le osservazioni all’interno dei gruppi sono state ottenute mediante campionamento casuale.
Leggi questo articolo per maggiori dettagli su come verificare queste ipotesi.
ANOVA unidirezionale: il processo
Un’ANOVA unidirezionale utilizza le seguenti ipotesi nulle e alternative:
- H 0 (ipotesi nulla): μ 1 = μ 2 = μ 3 = … = μ k (tutte le medie della popolazione sono uguali)
- H 1 (ipotesi alternativa): almeno una media della popolazione è diversa riposo
In genere utilizzerai alcuni software statistici (come R, Excel, Stata, SPSS, ecc.) per eseguire ANOVA unidirezionale perché è noioso eseguirlo manualmente.
Indipendentemente dal software utilizzato, riceverai come output la seguente tabella:
| Fonte | Somma dei quadrati (SS) | df | Quadrati medi (MS) | F | P |
|---|---|---|---|---|---|
| Trattamento | RSS | df r | MSR | MSR/MSE | F df r , df e |
| Errore | ESS | df e | MSE | ||
| Totale | OHS | dft |
Oro:
- SSR: regressione della somma dei quadrati
- SSE: somma dei quadrati degli errori
- SST: somma totale dei quadrati (SST = SSR + SSE)
- df r : gradi di libertà di regressione (df r = k-1)
- df e : gradi di libertà errore (df e = nk)
- df t : gradi di libertà totali (df t = n-1)
- k: numero totale di gruppi
- n: osservazioni totali
- MSR: regressione quadratica media (MSR = SSR/df r )
- MSE: errore quadratico medio (MSE = SSE/df e )
- F: La statistica del test F (F = MSR/MSE)
- p: Il valore p che corrisponde a F dfr, dfe
Se il valore p è inferiore al livello di significatività scelto (ad esempio 0,05), allora è possibile rifiutare l’ipotesi nulla e concludere che almeno una delle medie della popolazione è diversa dalle altre.
Nota: se si rifiuta l’ipotesi nulla, ciò indica che almeno una delle medie della popolazione è diversa dalle altre, ma la tabella ANOVA non specifica quali medie della popolazione sono diverse. Per determinarlo, è necessario eseguire test post hoc , chiamati anche test di “confronto multiplo”.
ANOVA unidirezionale: esempio
Supponiamo di voler sapere se tre diversi programmi di preparazione al test portano o meno a punteggi medi diversi in un dato esame. Per testarlo, reclutiamo 30 studenti per partecipare a uno studio e li dividiamo in tre gruppi.
Gli studenti di ciascun gruppo vengono assegnati in modo casuale a utilizzare uno dei tre programmi di preparazione al test per le tre settimane successive per prepararsi a un esame. Alla fine delle tre settimane, tutti gli studenti sostengono lo stesso esame.
Di seguito sono riportati i risultati degli esami per ciascun gruppo:

Per eseguire un’ANOVA unidirezionale su questi dati, utilizzeremo il calcolatore ANOVA unidirezionale delle statistiche con il seguente input:

Dalla tabella di output, vediamo che la statistica del test F è 2,358 e il corrispondente valore p è 0,11385 .

Poiché questo valore p non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla.
Ciò significa che non abbiamo prove sufficienti per affermare che esiste una differenza statisticamente significativa tra i punteggi medi degli esami dei tre gruppi.
Risorse addizionali
I seguenti articoli spiegano come eseguire un’ANOVA unidirezionale utilizzando diversi software statistici:
Come eseguire ANOVA unidirezionale in Excel
Come eseguire l’ANOVA unidirezionale in R
Come eseguire ANOVA unidirezionale in Python
Come eseguire ANOVA unidirezionale in SAS
Come eseguire l’ANOVA unidirezionale in SPSS
Come eseguire l’ANOVA unidirezionale in Stata
Come eseguire l’ANOVA unidirezionale su una calcolatrice TI-84
Calcolatore ANOVA unidirezionale online