Come eseguire l'anova unidirezionale in spss

Un’ANOVA unidirezionale viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi indipendenti.

Questo tipo di test è chiamato ANOVA unidirezionale perché analizziamo l’impatto di una variabile predittrice su una variabile di risposta.

Se fossimo invece interessati all’impatto di due variabili predittive su una variabile di risposta, potremmo eseguire un’ANOVA a due vie .

Questo tutorial spiega come eseguire un’ANOVA unidirezionale in SPSS.

Esempio: ANOVA unidirezionale in SPSS

Supponiamo che un ricercatore recluti 30 studenti per partecipare a uno studio. Agli studenti viene assegnato in modo casuale l’utilizzo di una delle tre tecniche di studio il mese successivo per prepararsi a un esame. Alla fine del mese tutti gli studenti sostengono lo stesso test.

I risultati dei test degli studenti sono mostrati di seguito:

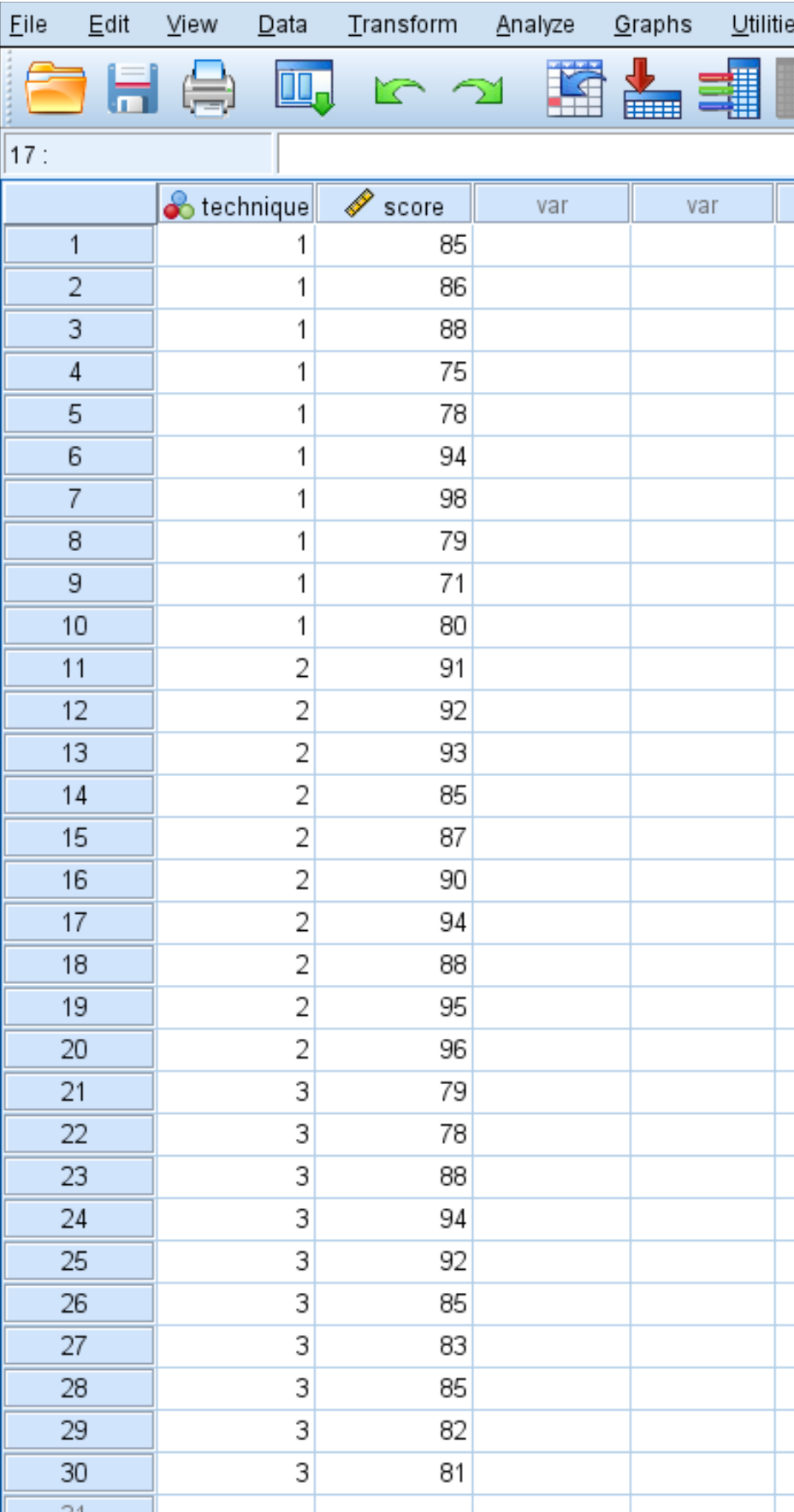
Utilizzare i passaggi seguenti per eseguire un’ANOVA unidirezionale per determinare se i punteggi medi sono gli stessi nei tre gruppi.

Passaggio 1: visualizzare i dati.

Per prima cosa creeremo dei boxplot per visualizzare la distribuzione dei punteggi dei test per ciascuna delle tre tecniche di studio. Fare clic sulla scheda Grafici , quindi su Generatore di grafici .

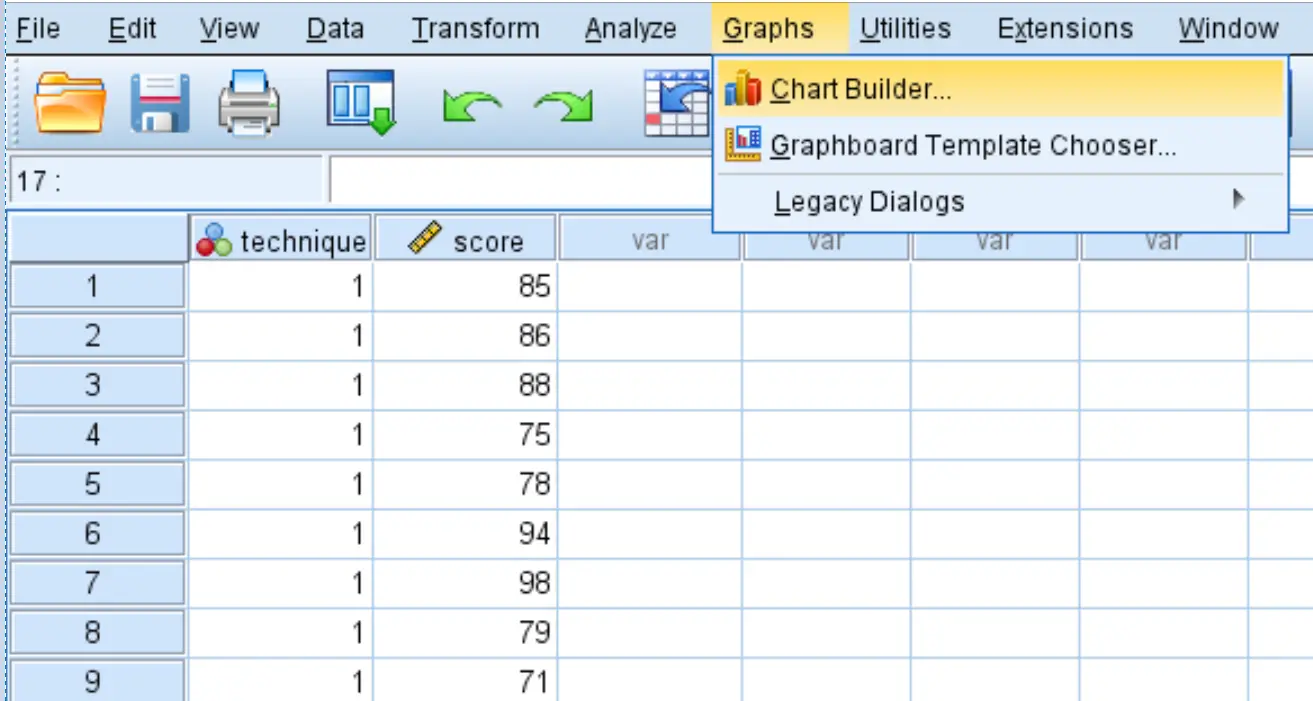
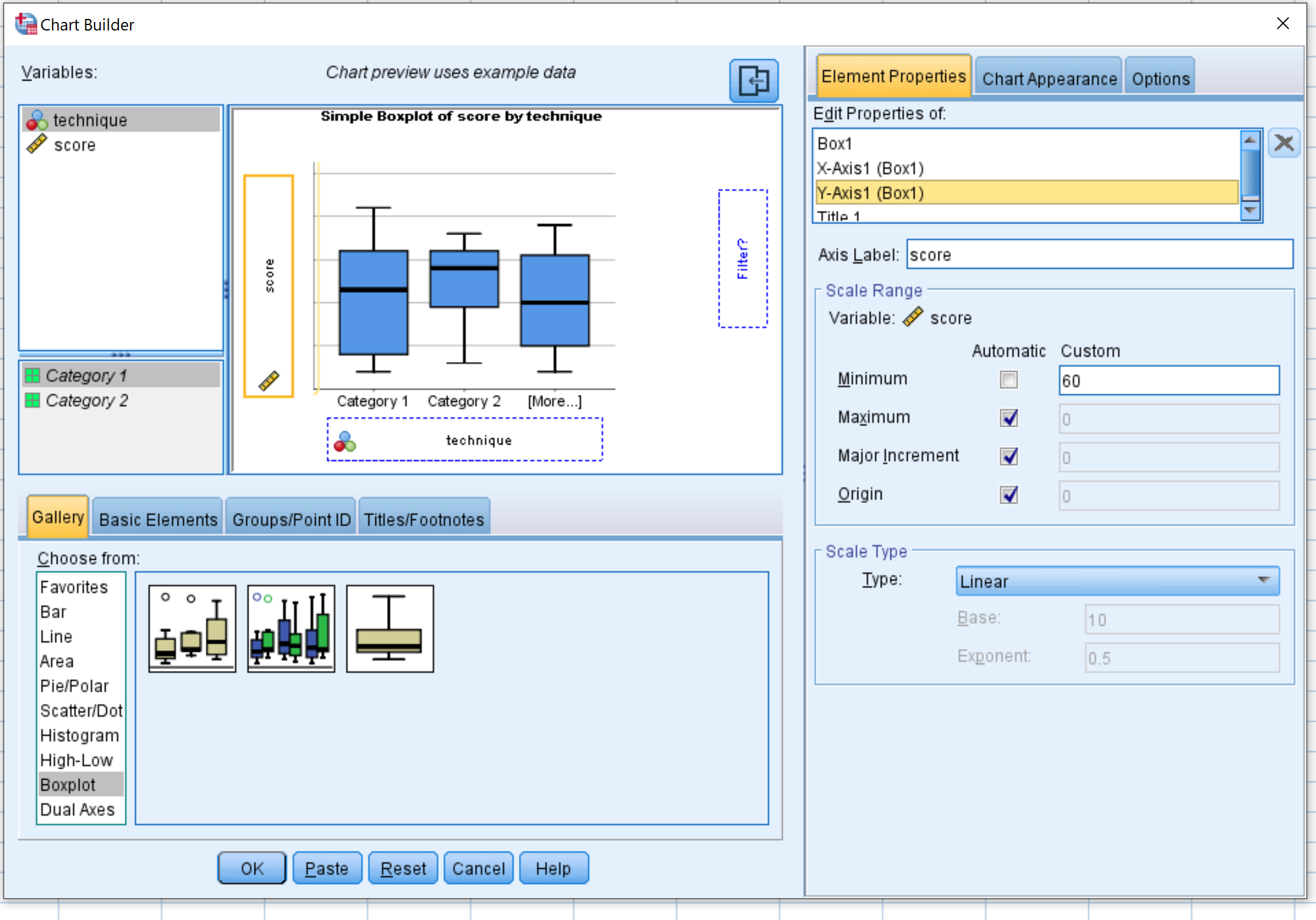
Selezionare Boxplot nella finestra Scegli da:. Quindi trascina il primo grafico denominato Boxplot semplice nella finestra di modifica principale. Trascina la variabile tecnica sull’asse x e il punteggio sull’asse y.

Fare quindi clic su Proprietà elemento e quindi su Asse Y1 . Modificare il valore minimo in 60. Quindi fare clic su OK .

Appariranno i seguenti boxplot:

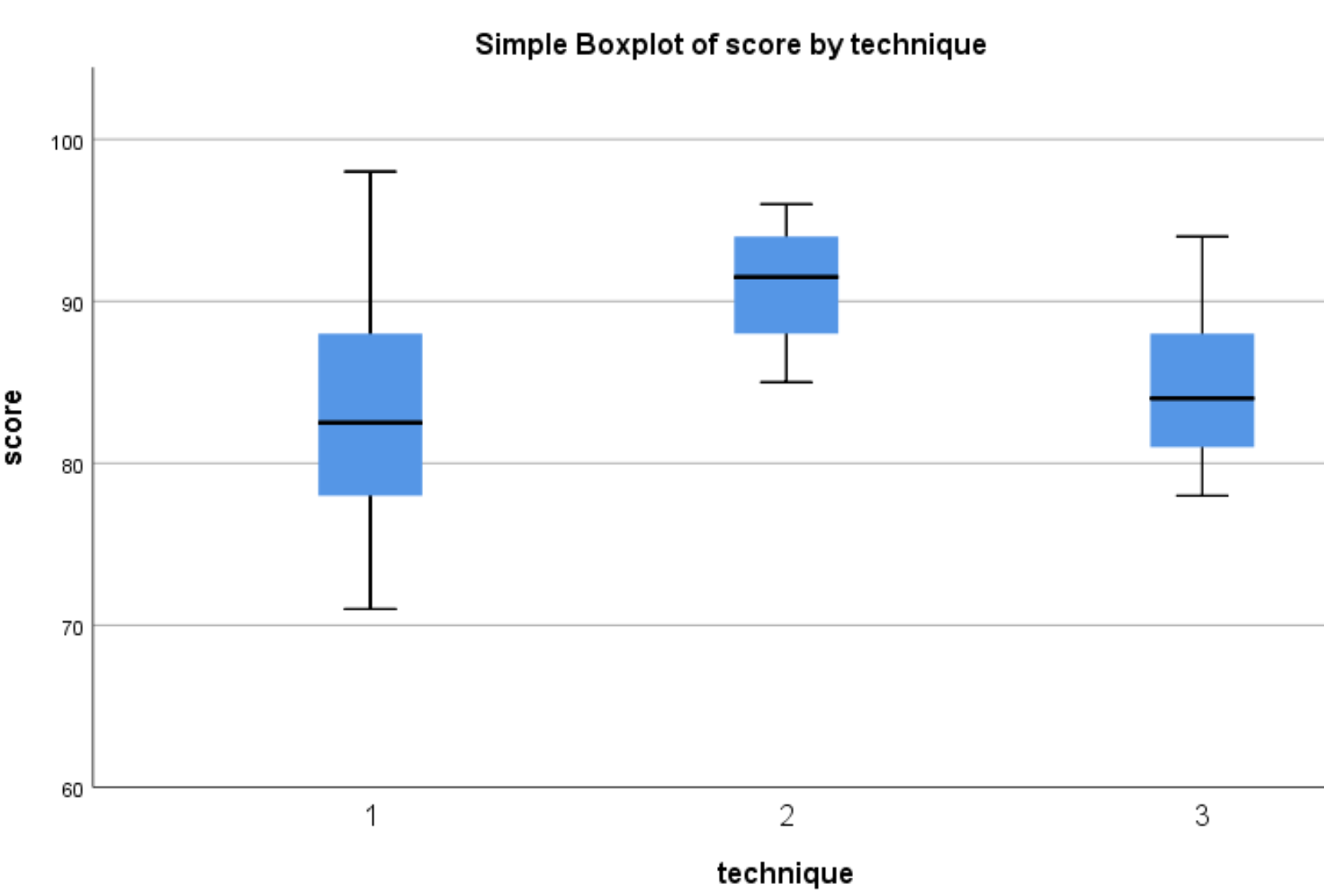
Possiamo vedere che la distribuzione dei punteggi dei test tende ad essere più alta per gli studenti che hanno utilizzato la Tecnica 2 rispetto agli studenti che hanno utilizzato le Tecniche 1 e 3. Per determinare se queste differenze di punteggio sono statisticamente significative, eseguiremo un’ANOVA unidirezionale.

Passaggio 2: eseguire un’ANOVA unidirezionale.

Fare clic sulla scheda Analizza , quindi su Confronta medie , quindi su ANOVA unidirezionale .

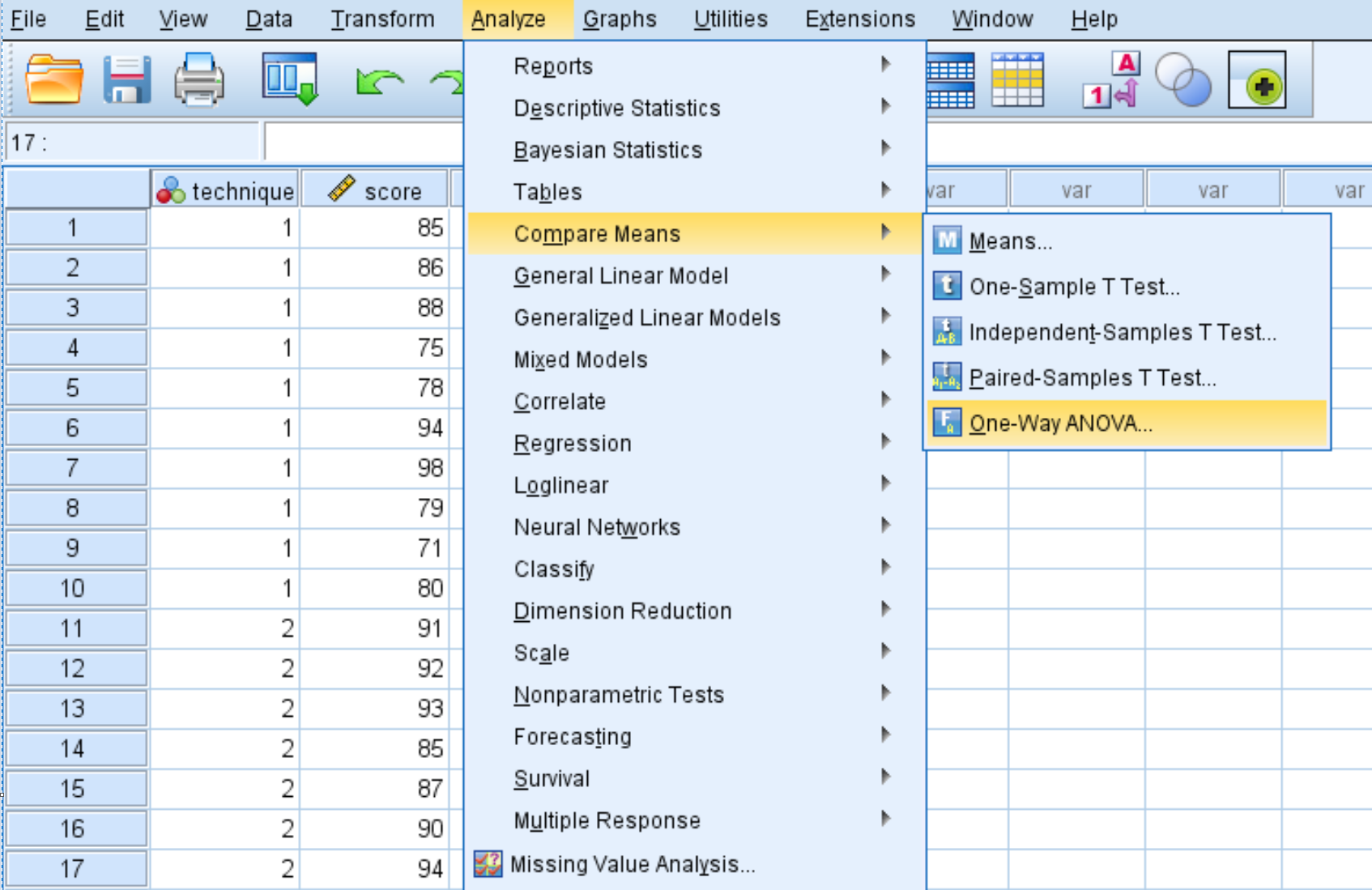
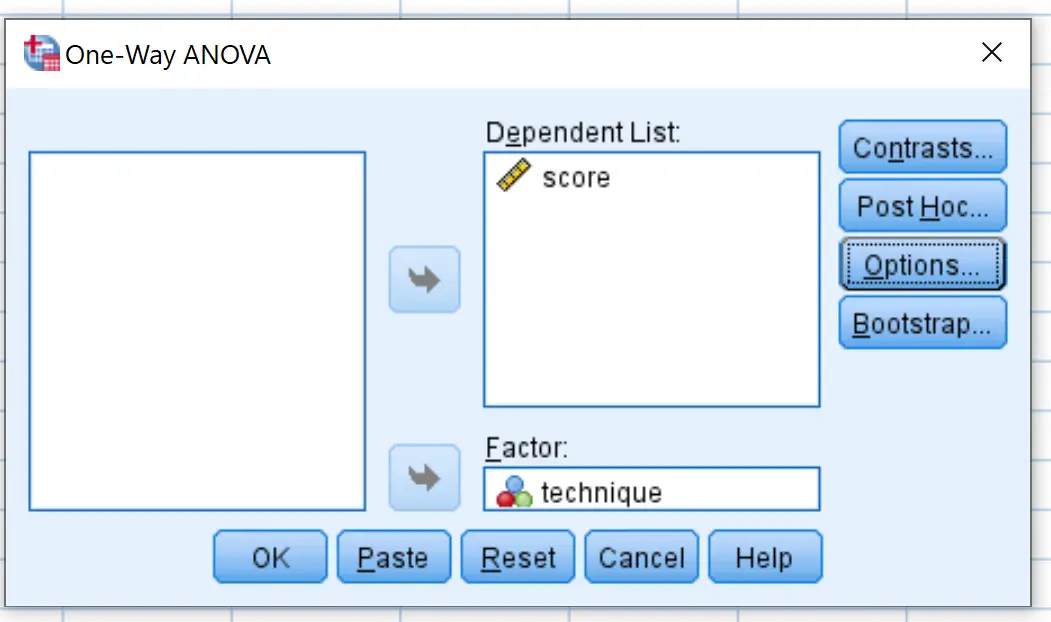
Nella nuova finestra che appare, posiziona il punteggio della variabile nella casella denominata Elenco dipendente e la tecnica della variabile nella casella denominata Fattore.

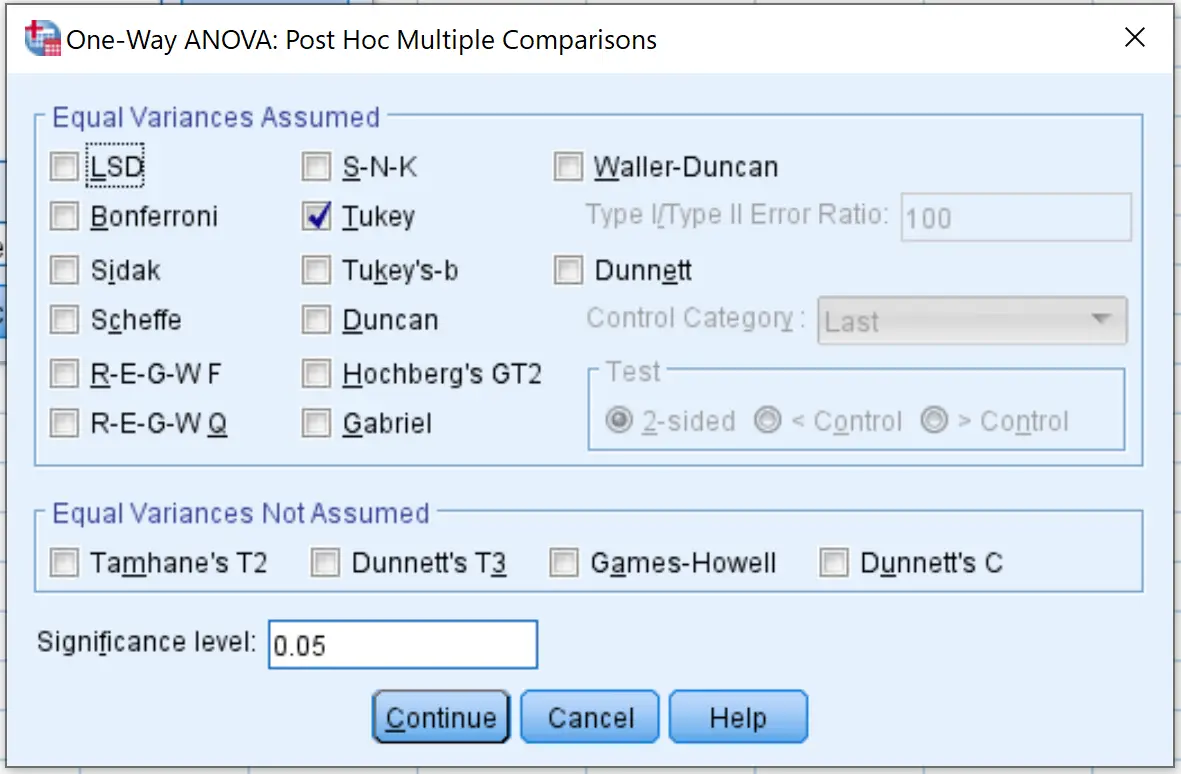
Quindi fare clic su Post Hoc e selezionare la casella accanto a Tukey . Quindi fare clic su Continua .

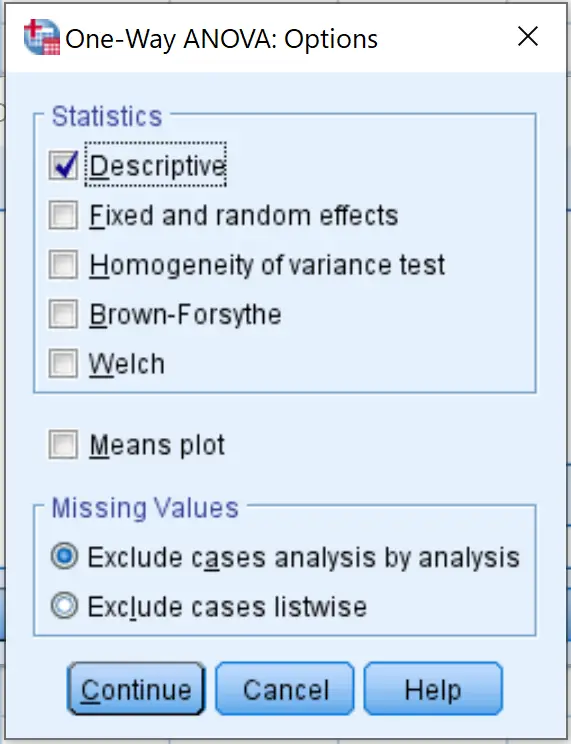
Quindi fare clic su Opzioni e selezionare la casella accanto a Descrittivo . Quindi fare clic su Continua .

Infine, fare clic su OK .

Passaggio 3: interpretare il risultato.

Dopo aver fatto clic su OK , verranno visualizzati i risultati ANOVA unidirezionali. Ecco come interpretare il risultato:

Descrizione della tabella

Questa tabella mostra le statistiche descrittive per ciascuno dei tre gruppi nel nostro set di dati.

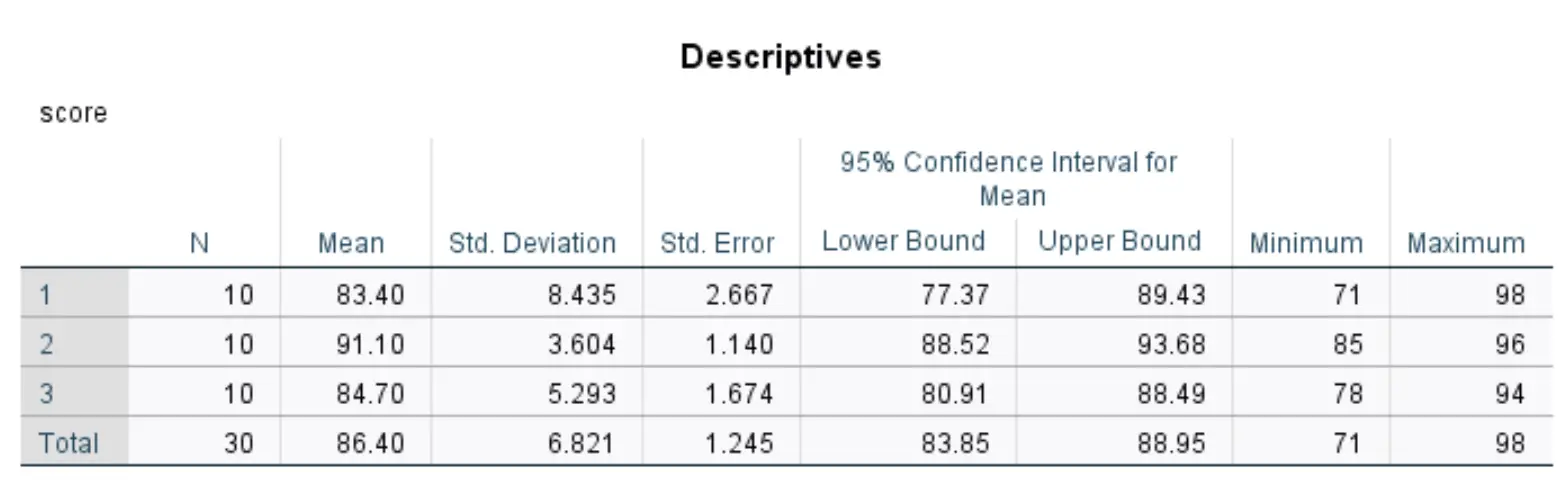
I dati più rilevanti includono:

• N: il numero di studenti in ciascun gruppo.
• Media: il punteggio medio del test per ciascun gruppo.
• Standard. Deviazione: deviazione standard dei risultati del test per ciascun gruppo.

Tabella ANOVA

Questa tabella mostra i risultati dell’ANOVA unidirezionale:

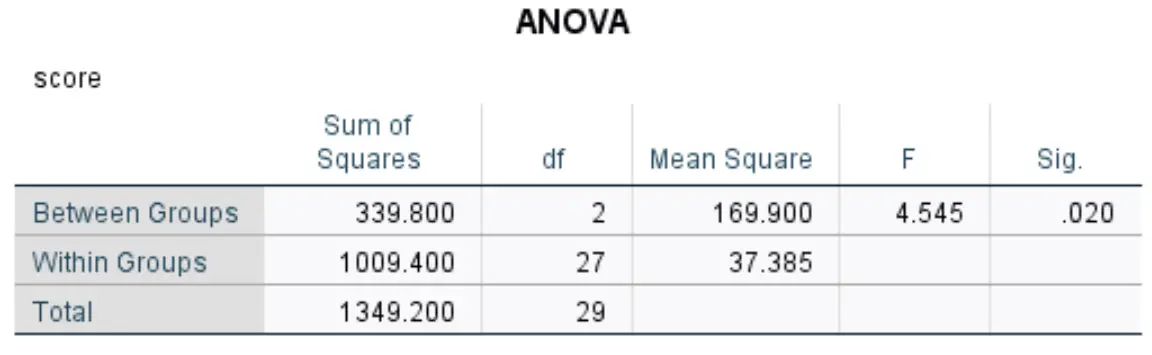
I dati più rilevanti includono:

• F: la statistica F complessiva.
• Sig: il valore p che corrisponde alla statistica F (4.545) con il numeratore df (2) e il denominatore df (27). In questo caso, il valore p risulta essere 0,020 .

Ricordiamo che un’ANOVA unidirezionale utilizza le seguenti ipotesi nulle e alternative:

• H ₀ (ipotesi nulla): μ ₁ = μ ₂ = μ ₃ = … = μ _k (tutte le medie della popolazione sono uguali)
• H _A (ipotesi alternativa): almeno una media della popolazione è diversa   riposo

Poiché il valore p della tabella ANOVA è inferiore a 0,05, abbiamo prove sufficienti per rifiutare l’ipotesi nulla e concludere che almeno una delle medie del gruppo è diversa dalle altre.

Per sapere esattamente quali medie di gruppo differiscono l’una dall’altra, possiamo fare riferimento all’ultima tabella del risultato ANOVA.

Tabella di confronto multiplo

Questa tabella mostra i confronti multipli post-hoc di Tukey tra ciascuno dei tre gruppi. Siamo interessati principalmente al Sig. colonna, che mostra i valori p per le differenze nelle medie tra ciascun gruppo:

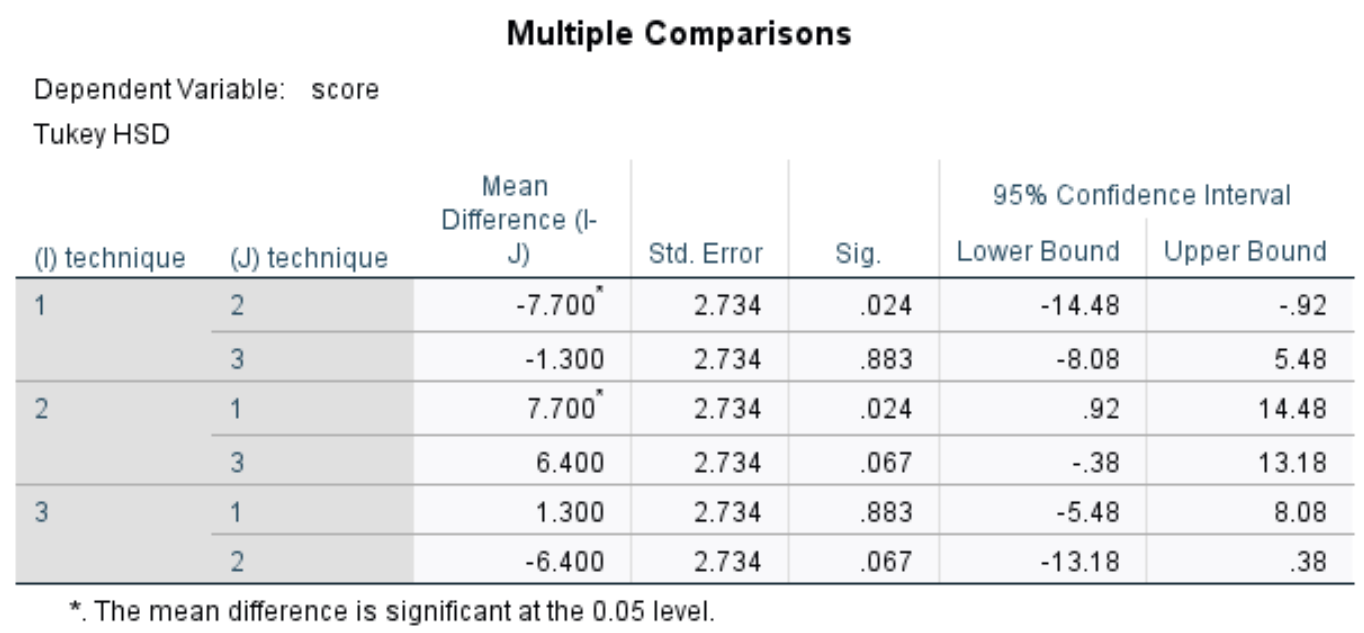
Nella tabella possiamo vedere i valori p per i seguenti confronti:

• Tecnica 1 contro 2: | valore p = 0,024
• Tecnica 1 contro 3 | valore p = 0,883
• Tecnica 2 contro 3 | valore p = 0,067

L’unico confronto di gruppo con un valore p inferiore a 0,05 è tra la Tecnica 1 e la Tecnica 2.

Questo ci dice che esiste una differenza statisticamente significativa nei punteggi medi dei test tra gli studenti che hanno utilizzato la Tecnica 1 e quelli che hanno utilizzato la Tecnica 2.

Tuttavia, non vi è alcuna differenza statisticamente significativa tra le tecniche 1 e 3, né tra le tecniche 2 e 3.

Passaggio 4: riportare i risultati.

Infine, possiamo riportare i risultati dell’ANOVA unidirezionale. Ecco un esempio di come eseguire questa operazione:

È stata eseguita un’ANOVA unidirezionale per determinare se tre diverse tecniche di studio portassero a risultati di test diversi.

Un totale di 10 studenti hanno utilizzato ciascuna delle tre tecniche di studio per un mese prima di sostenere tutti lo stesso test.

Un’ANOVA unidirezionale ha rivelato che c’era una differenza statisticamente significativa nei punteggi dei test tra almeno due gruppi (F(2, 27) = 4,545, p = 0,020).

Il test di Tukey per confronti multipli ha rivelato che i punteggi medi dei test erano significativamente diversi tra gli studenti che hanno utilizzato la Tecnica 1 e la Tecnica 2 (p = 0,024, IC 95% = [-14,48, -0,92]).

Non c’era differenza statisticamente significativa tra i punteggi per le tecniche 1 e 3 (p = 0,883) o tra i punteggi per le tecniche 2 e 3 (p = 0,067).