Come eseguire la regressione polinomiale utilizzando scikit-learn

La regressione polinomiale è una tecnica che possiamo utilizzare quando la relazione tra una variabile predittore e una variabile di risposta non è lineare.

Questo tipo di regressione assume la forma:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

dove h è il “grado” del polinomio.

Il seguente esempio passo passo mostra come eseguire la regressione polinomiale in Python utilizzando sklearn.

Passaggio 1: creare i dati

Innanzitutto, creiamo due array NumPy per contenere i valori di un predittore e di una variabile di risposta:

 import matplotlib. pyplot as plt
import numpy as np

#define predictor and response variables
x = np. array ([2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12])
y = np. array ([18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29])

#create scatterplot to visualize relationship between x and y
plt. scatter (x,y)

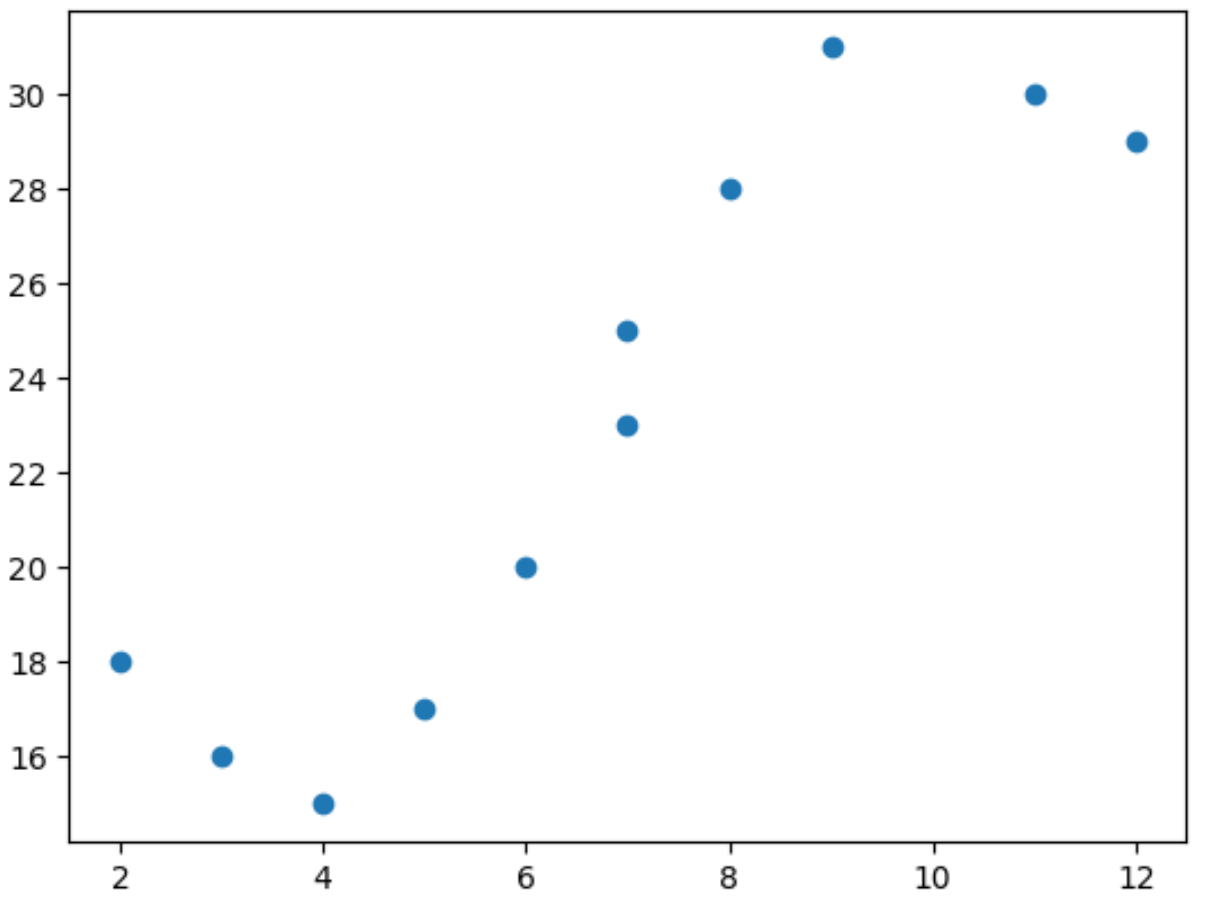
Dal grafico a dispersione possiamo vedere che la relazione tra xey non è lineare.

È quindi una buona idea adattare ai dati un modello di regressione polinomiale per catturare la relazione non lineare tra le due variabili.

Passaggio 2: adattare il modello di regressione polinomiale

Il codice seguente mostra come utilizzare le funzioni sklearn per adattare un modello di regressione polinomiale di grado 3 a questo set di dati:

 from sklearn. preprocessing import PolynomialFeatures
from sklearn. linear_model import LinearRegression

#specify degree of 3 for polynomial regression model
#include bias=False means don't force y-intercept to equal zero
poly = PolynomialFeatures(degree= 3 , include_bias= False )

#reshape data to work properly with sklearn
poly_features = poly. fit_transform ( x.reshape (-1, 1))

#fit polynomial regression model
poly_reg_model = LinearRegression()
poly_reg_model. fit (poly_features,y)

#display model coefficients
print (poly_reg_model. intercept_ , poly_reg_model. coef_ )

33.62640037532282 [-11.83877127 2.25592957 -0.10889554]

Utilizzando i coefficienti del modello mostrati nell’ultima riga, possiamo scrivere l’equazione di regressione polinomiale adattata come segue:

y = -0,109x ³ + 2,256x ² – 11,839x + 33,626

Questa equazione può essere utilizzata per trovare il valore atteso della variabile di risposta dato un dato valore della variabile prevista.

Ad esempio, se x è 4, il valore atteso per la variabile di risposta, y, sarebbe 15,39:

y = -0,109(4) ³ + 2,256(4) ² – 11,839(4) + 33,626= 15,39

Nota : per adattare un modello di regressione polinomiale con un grado diverso, è sufficiente modificare il valore dell’argomento grado nella funzione PolynomialFeatures() .

Passaggio 3: Visualizza il modello di regressione polinomiale

Infine, possiamo creare un semplice grafico per visualizzare il modello di regressione polinomiale adattato ai punti dati originali:

 #use model to make predictions on response variable
y_predicted = poly_reg_model. predict (poly_features)

#create scatterplot of x vs. y
plt. scatter (x,y)

#add line to show fitted polynomial regression model
plt. plot (x,y_predicted,color=' purple ')

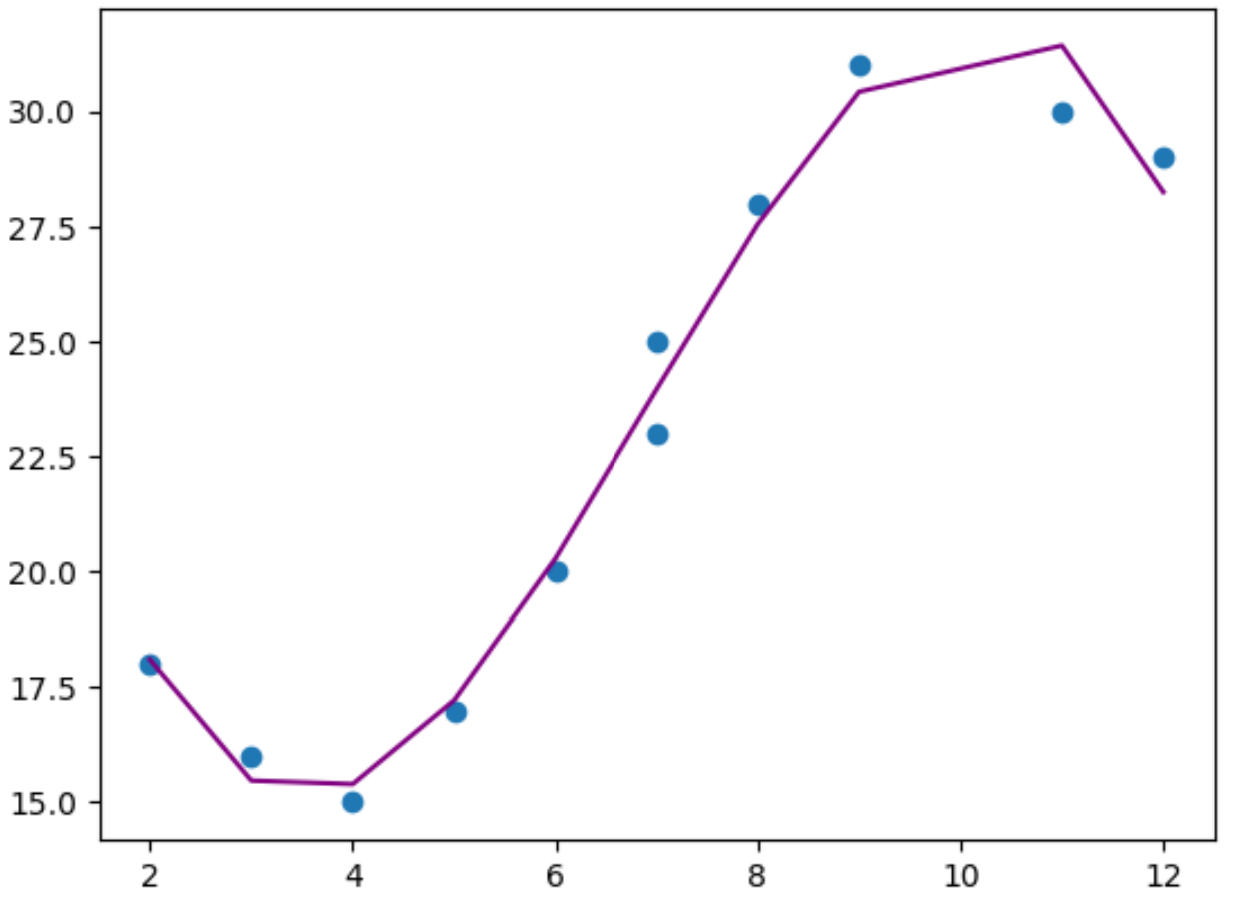
Dal grafico, possiamo vedere che il modello di regressione polinomiale sembra adattarsi bene ai dati senza adattarli eccessivamente .

Nota : puoi trovare la documentazione completa per la funzione sklearn PolynomialFeatures() qui .

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni utilizzando sklearn:

Come estrarre i coefficienti di regressione da sklearn
Come calcolare la precisione bilanciata utilizzando sklearn
Come interpretare il rapporto di classificazione in Sklearn