Distribuzione di bernoulli e distribuzione binomiale: qual è la differenza?

Una variabile casuale segue una distribuzione di Bernoulli se ha solo due possibili risultati: 0 o 1.

Ad esempio, supponiamo di lanciare una moneta una volta. Lasciamo che p . Ciò significa che la probabilità che esca croce è 1- p .

Quindi, potremmo scrivere:

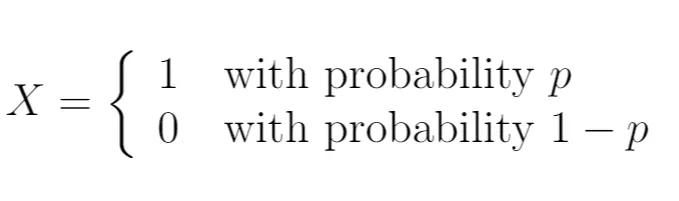
In questo caso, la variabile casuale X segue una distribuzione di Bernoulli. Può assumere solo due valori possibili.

Ora, se lanciamo una moneta più volte, la somma delle variabili casuali di Bernoulli seguirà una distribuzione binomiale.

Ad esempio, supponiamo di lanciare una moneta 5 volte e di voler conoscere la probabilità che esca testa k volte. Sembra la variabile casuale

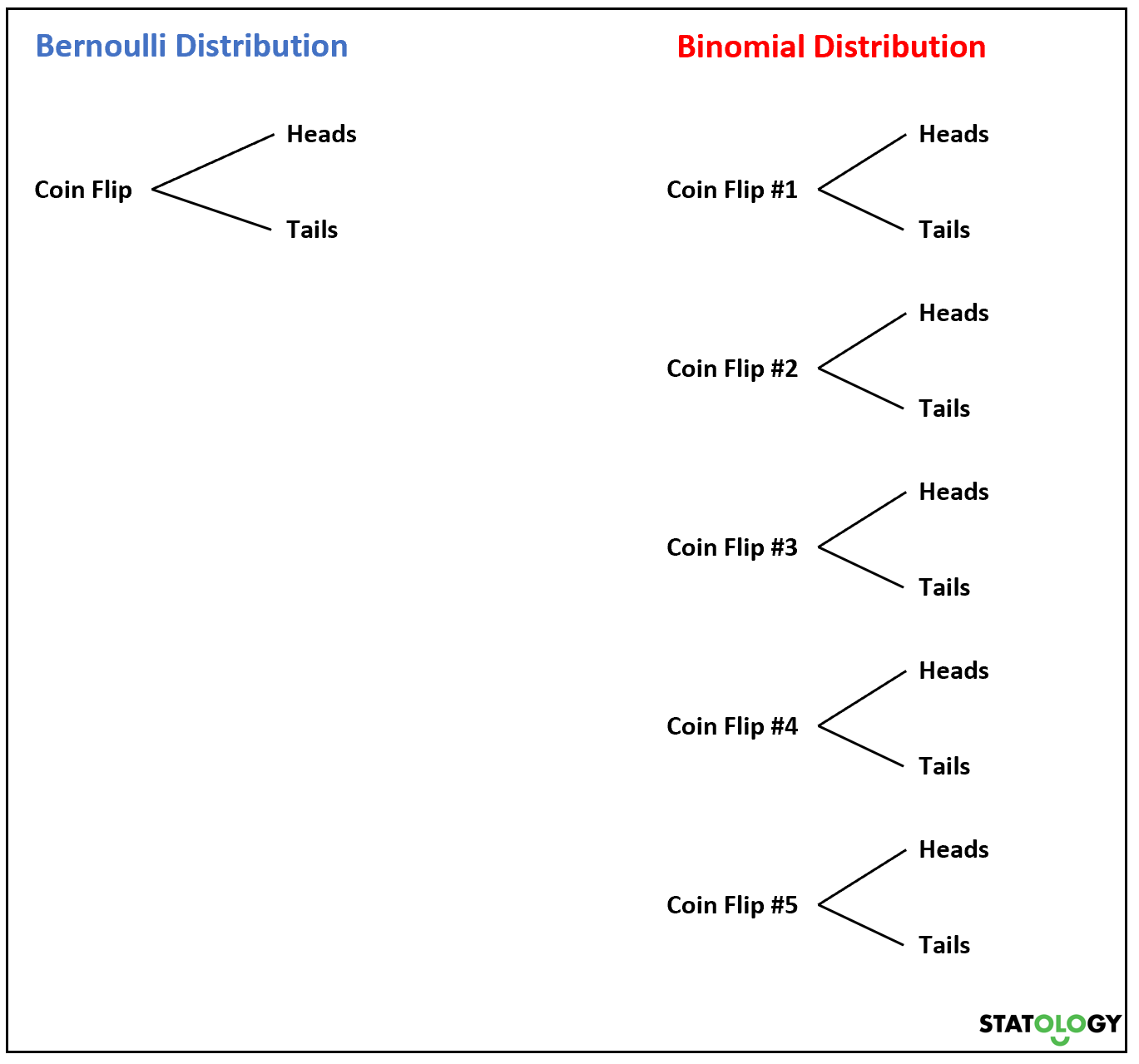
Se una variabile casuale X segue una distribuzione binomiale, la probabilità che X = k successo può essere trovata con la seguente formula:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Oro:

• n: numero di prove
• k: numero di successi
• p: probabilità di successo in una determinata prova
• _n C _k : il numero di modi per ottenere k successi in n prove

Ad esempio, supponiamo di lanciare una moneta 3 volte. Possiamo usare la formula sopra per determinare la probabilità di ottenere 0 testa durante questi 3 lanci:

P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125

Quando n = 1 prova, la distribuzione binomiale è equivalente alla distribuzione di Bernoulli.

Note importanti

Ecco alcune note importanti riguardanti la distribuzione Bernoulli e binomiale:

1. Una variabile casuale che segue una distribuzione Bernoulli può assumere solo due valori possibili, ma una variabile casuale che segue una distribuzione binomiale può assumere diversi valori.

Ad esempio, nel lancio di una moneta avremo 0 o 1 testa. Tuttavia, in una serie di 5 estrazioni potremmo avere 0, 1, 2, 3, 4 o 5 teste.

2. Affinché una variabile casuale segua una distribuzione binomiale, la probabilità di “successo” in ciascuna prova Bernoulli deve essere uguale e indipendente.

Ad esempio, se definiamo “successo” come ottenere testa, allora la probabilità di successo per ogni lancio è 0,5 e ogni lancio è indipendente: il risultato di un lancio non influenza il risultato di un altro.

Risorse addizionali

Un’introduzione agli esperimenti binomiali
Un’introduzione alla distribuzione binomiale
Comprendere la forma di una distribuzione binomiale