Distribuzioni distorte a sinistra o a destra

L’asimmetria è un modo per descrivere la simmetria di una distribuzione.

Una distribuzione è distorta se ha una “coda” sul lato sinistro della distribuzione:

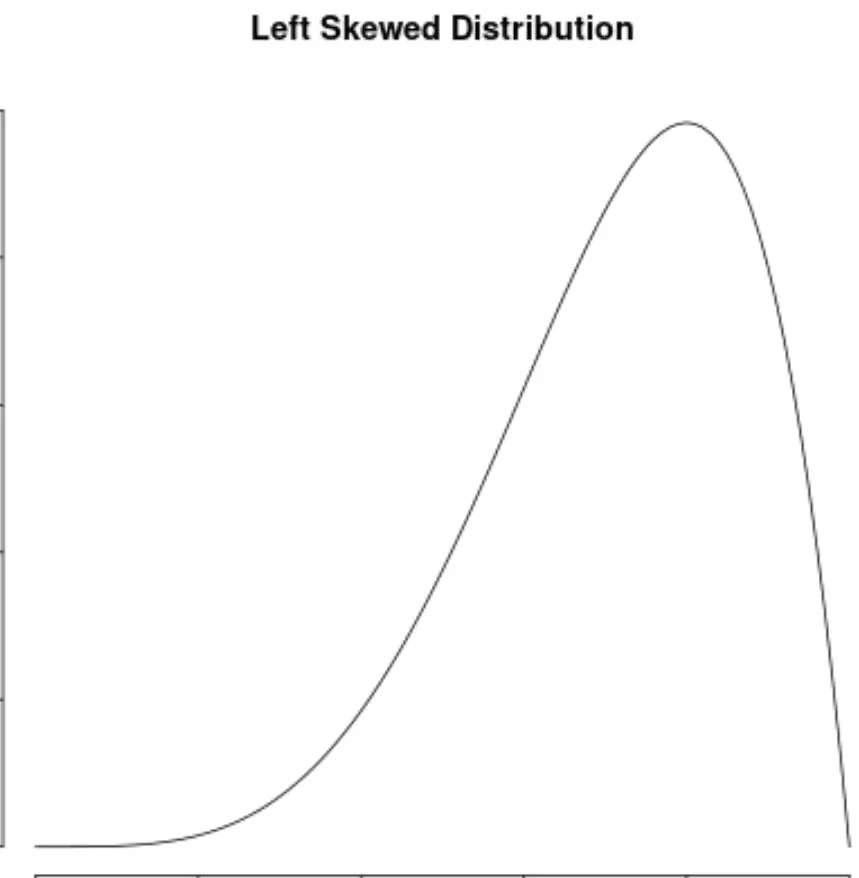
Una distribuzione è distorta a destra se ha una “coda” sul lato destro della distribuzione:

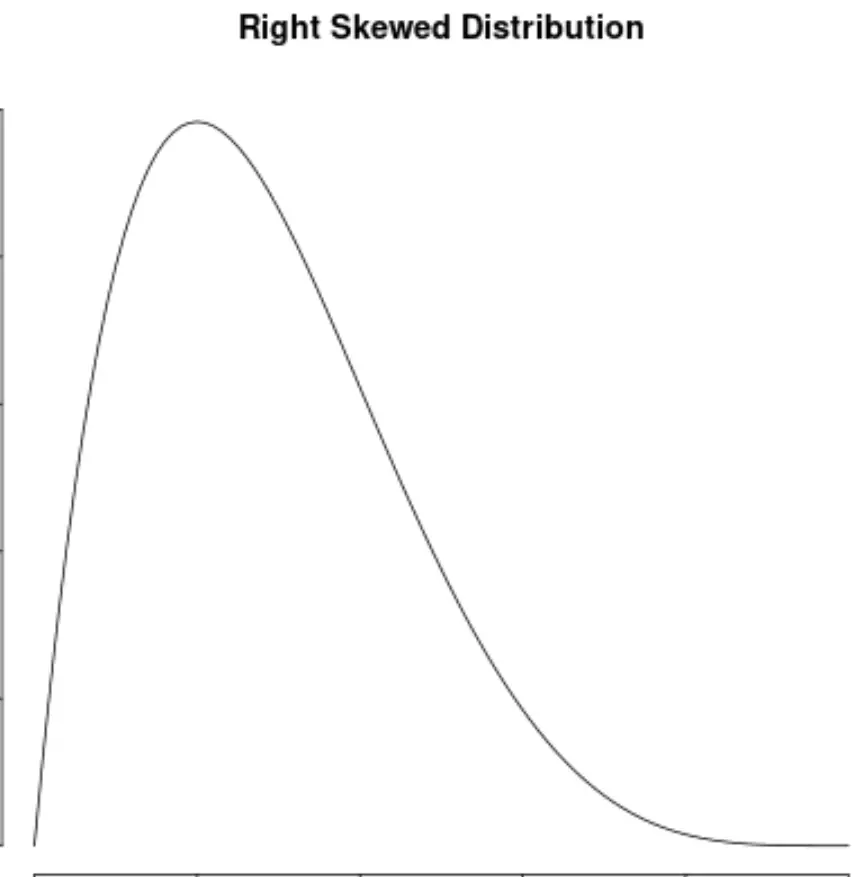
E una distribuzione non ha pregiudizi se è simmetrica su entrambi i lati:

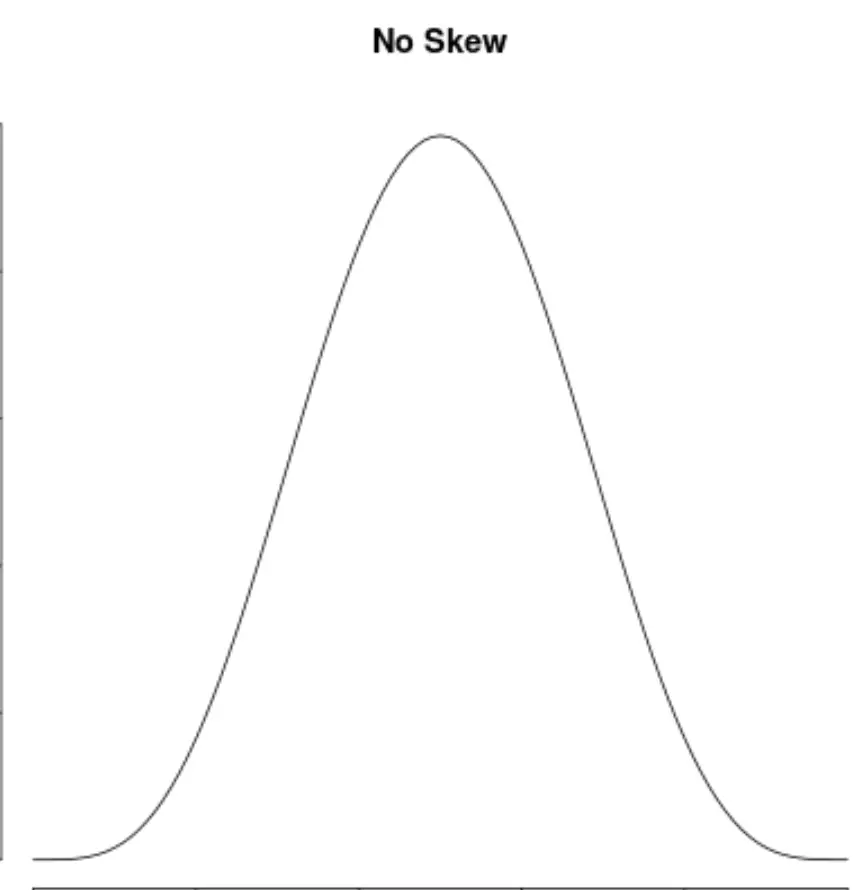
Si noti che le distribuzioni asimmetriche a sinistra sono talvolta chiamate distribuzioni “asimmetriche negativamente” e le distribuzioni asimmetriche a destra sono talvolta chiamate distribuzioni “asimmetriche positivamente”.

Proprietà delle distribuzioni asimmetriche

I seguenti diagrammi mostrano dove si trovano tipicamente la media, la mediana e la moda nelle diverse distribuzioni.

Distribuzione distorta a sinistra: media <mediana <modalità

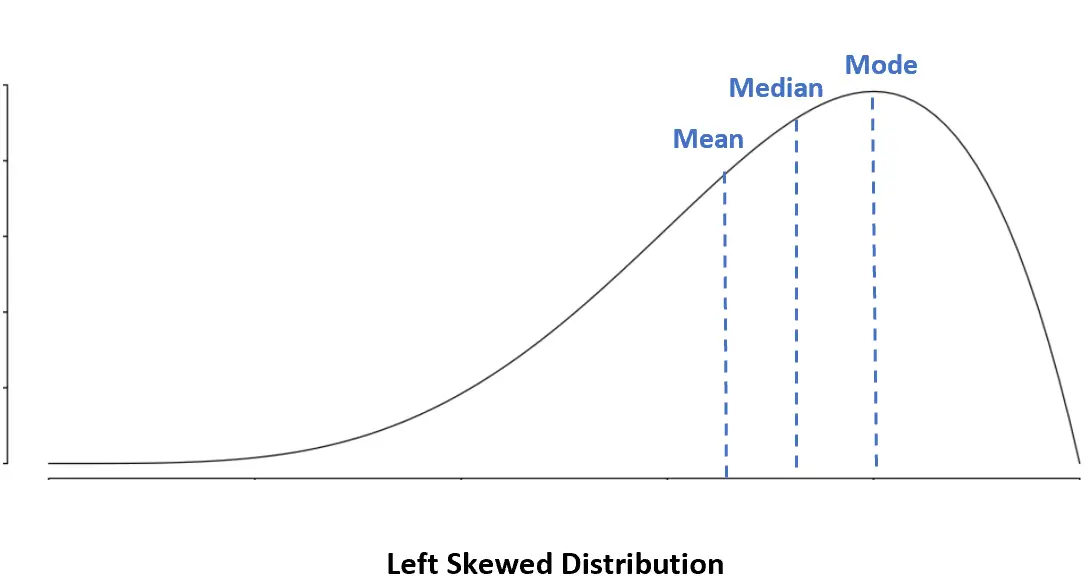
In una distribuzione distorta a sinistra, la media è inferiore alla mediana.

Distribuzione distorta a destra: Modalità < Mediana < Media

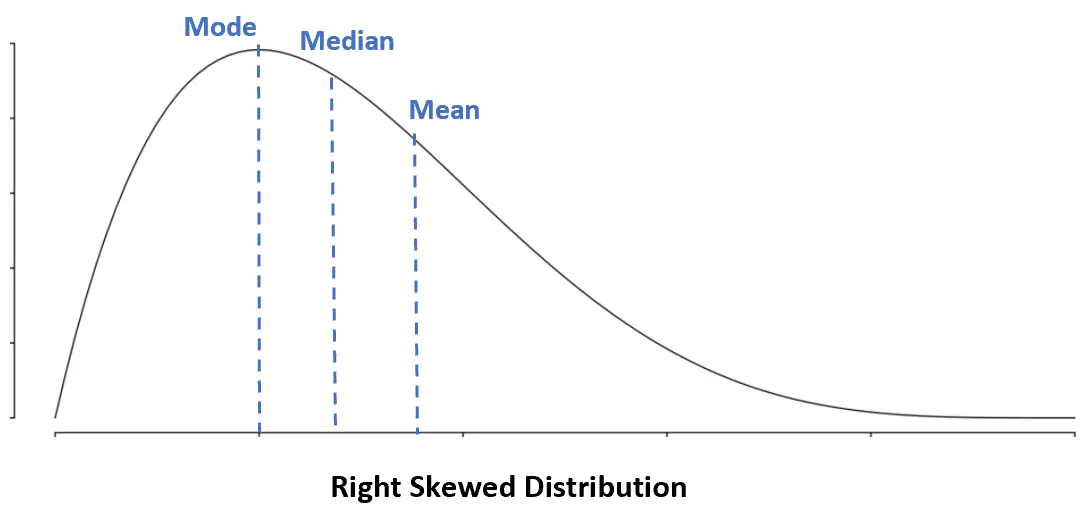
In una distribuzione distorta a destra, la media è maggiore della mediana.

Nessuna distorsione: media = mediana = modalità

In una distribuzione simmetrica media, mediana e moda sono tutte uguali.

Utilizzo dei box plot per visualizzare l’asimmetria

Un box plot è un tipo di grafico che visualizza il riepilogo di cinque cifre di un set di dati, che include:

• Il valore minimo
• Il primo quartile (il 25° percentile)
• Il valore mediano
• Il terzo quartile (il 75° percentile)
• Il valore massimo

Per realizzare un box plot, disegniamo un riquadro dal primo al terzo quartile. Successivamente, tracciamo una linea verticale in corrispondenza della mediana. Infine disegniamo i “baffi” dei quartili fino al valore minimo e massimo.

In base alla posizione del valore mediano nel boxplot, possiamo determinare se una distribuzione è distorta a sinistra, a destra o simmetrica.

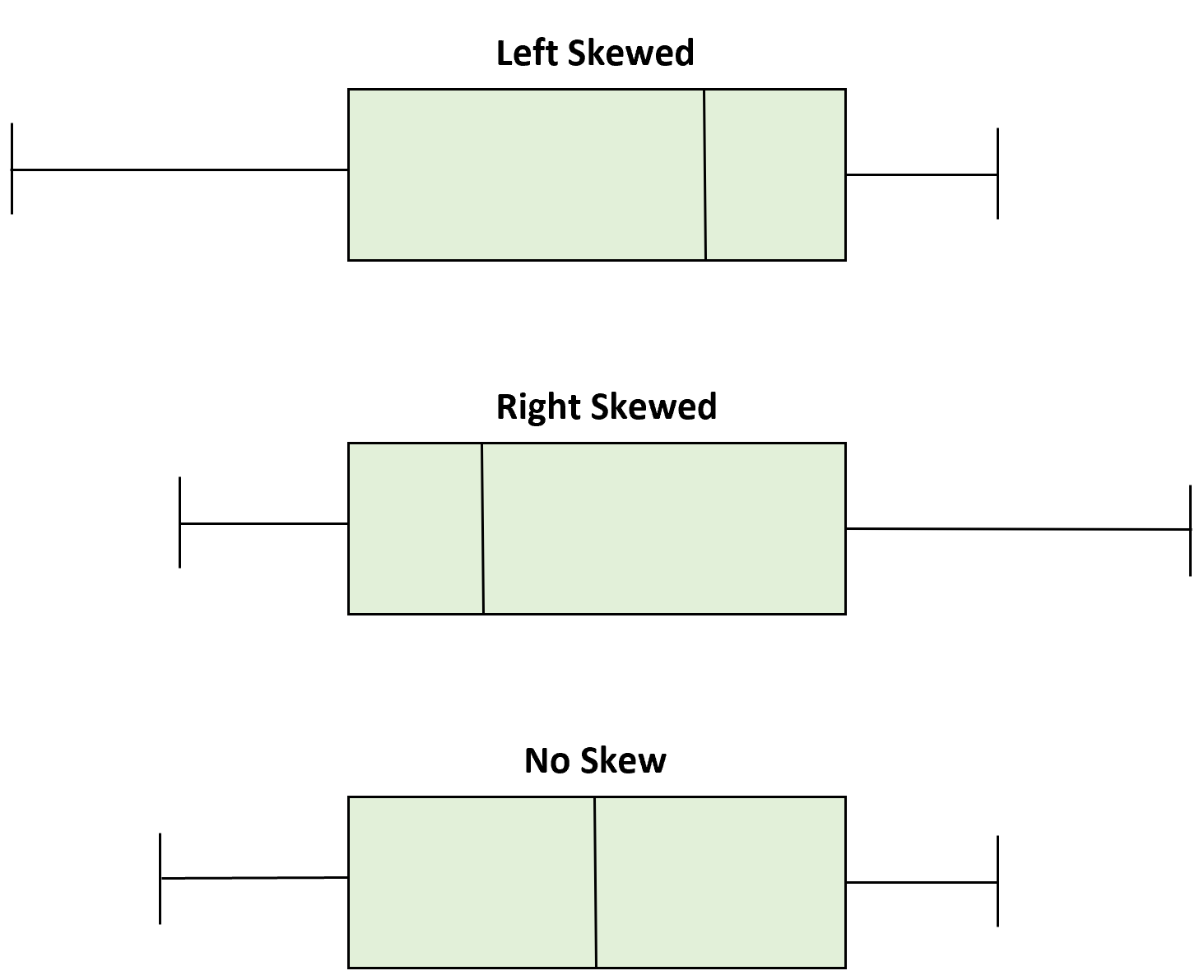
Quando la mediana è più vicina al fondo della scatola e il baffo è più corto all’estremità inferiore della scatola, la distribuzione è distorta a destra.

Quando la mediana è più vicina alla parte superiore della scatola e il baffo è più corto all’estremità superiore della scatola, la distribuzione rimane distorta.

Quando la mediana è al centro della scatola e i baffi sono approssimativamente uguali su ciascun lato, la distribuzione è simmetrica.

Esempi di distribuzioni asimmetriche

Ecco alcuni esempi concreti di distribuzioni asimmetriche.

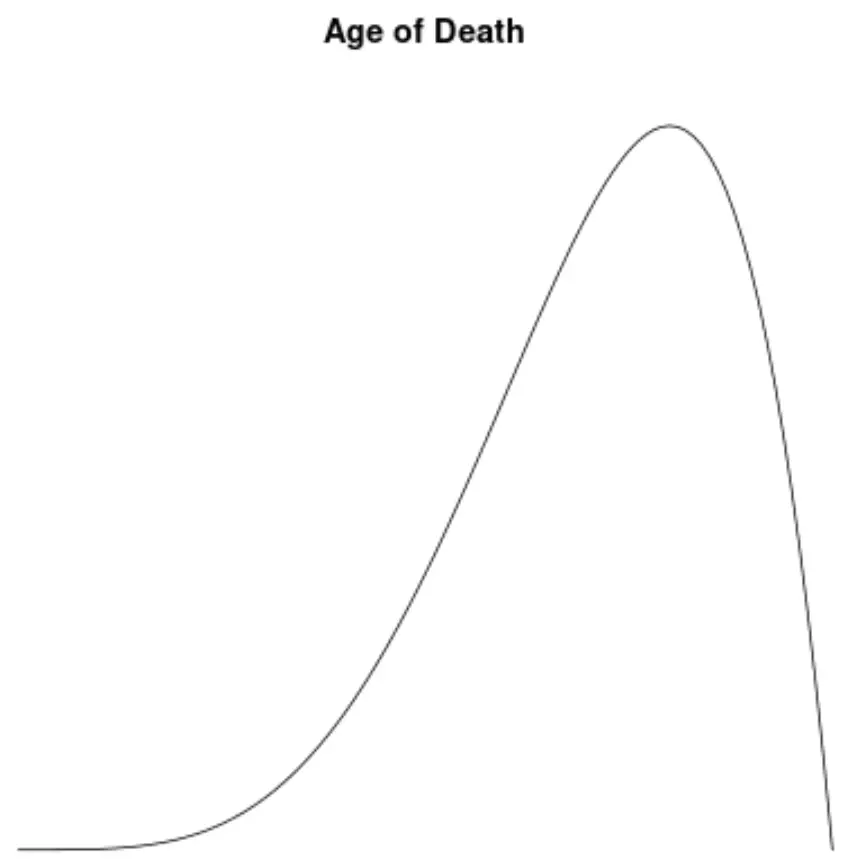
Distribuzione distorta a sinistra: la distribuzione dell’età dei decessi.

La distribuzione per età dei decessi nella maggior parte delle popolazioni è sbilanciata verso sinistra. La maggior parte delle persone vive tra i 70 e gli 80 anni, e sempre meno vivono al di sotto di questa età.

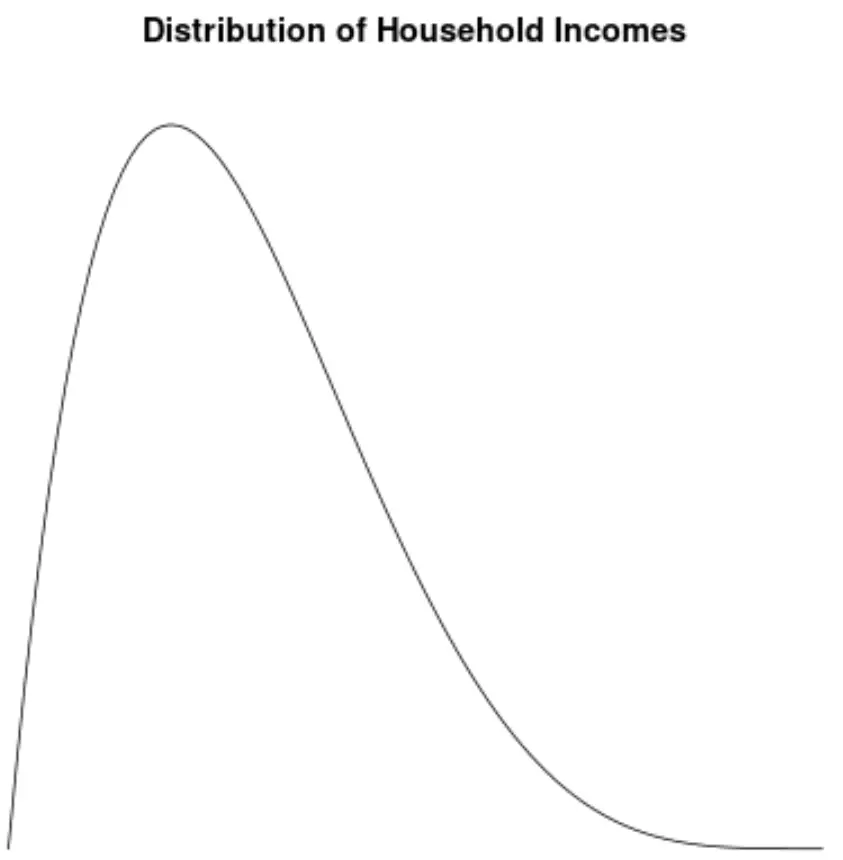
Distribuzione distorta a destra: la distribuzione del reddito familiare.

La distribuzione del reddito familiare negli Stati Uniti è sbilanciata verso destra, con la maggior parte delle famiglie che guadagna tra i 40.000 e gli 80.000 dollari all’anno, ma con una lunga coda destra di famiglie che guadagna molto di più.

No Skew: la distribuzione delle taglie maschili.

È noto che la dimensione dei maschi è approssimativamente normale e non presenta asimmetrie. Ad esempio, l’altezza media di un uomo negli Stati Uniti è di circa 69,1 pollici. La distribuzione dell’altezza è più o meno simmetrica, con alcuni più bassi e altri più alti.

Risorse addizionali

5 esempi di distribuzioni asimmetriche positivamente
5 esempi di distribuzioni asimmetriche negativamente
Come calcolare l’asimmetria in Excel
Come identificare l’asimmetria nei box plot