Binomio negativo vs poisson: come scegliere un modello di regressione

La regressione binomiale negativa e la regressione di Poisson sono due tipi di modelli di regressione da utilizzare quando la variabile di risposta è rappresentata da risultati di conteggio discreti.

Di seguito sono riportati alcuni esempi di variabili di risposta che rappresentano risultati di conteggio discreti:

• Il numero di studenti che si diplomano in un determinato programma
• Il numero di incidenti stradali in un determinato incrocio
• Il numero di partecipanti che completano una maratona
• Il numero di resi in un dato mese presso un negozio al dettaglio

Se la varianza è approssimativamente uguale alla media, allora un modello di regressione di Poisson generalmente si adatta bene a un set di dati.

Tuttavia, se la varianza è significativamente maggiore della media, un modello di regressione binomiale negativo è generalmente in grado di adattarsi meglio ai dati.

Esistono due tecniche che possiamo utilizzare per determinare se la regressione di Poisson o la regressione binomiale negativa è più appropriata per un dato set di dati:

1. Appezzamenti residui

Possiamo creare un grafico dei residui standardizzati rispetto ai valori previsti da un modello di regressione.

Se la maggior parte dei residui standardizzati è compresa tra -2 e 2, probabilmente è appropriato un modello di regressione di Poisson.

Tuttavia, se molti residui non rientrano in questo intervallo, un modello di regressione binomiale negativo probabilmente fornirà una soluzione migliore.

2. Test del rapporto di verosimiglianza

Possiamo adattare un modello di regressione di Poisson e un modello di regressione binomiale negativa allo stesso set di dati e quindi eseguire un test del rapporto di verosimiglianza.

Se il valore p del test è inferiore a un certo livello di significatività (ad esempio 0,05), allora possiamo concludere che il modello di regressione binomiale negativa fornisce un adattamento significativamente migliore.

L’esempio seguente mostra come utilizzare queste due tecniche in R per determinare se è meglio utilizzare un modello di regressione di Poisson o di regressione binomiale negativa per un determinato set di dati.

Esempio: regressione binomiale negativa vs regressione di Poisson

Supponiamo di voler sapere quante borse di studio riceve un giocatore di baseball delle scuole superiori di una determinata contea in base alla sua divisione scolastica (“A”, “B” o “C”) e al suo voto scolastico. esame di ammissione all’università (misurato da 0 a 100). ).

Utilizzare i passaggi seguenti per determinare se un modello di regressione binomiale negativa o un modello di regressione di Poisson fornisce un adattamento migliore ai dati.

Passaggio 1: creare i dati

Il codice seguente crea il set di dati con cui lavoreremo, che include dati su 1.000 giocatori di baseball:

 #make this example reproducible
set. seeds (1)

#create dataset
data <- data. frame (offers = c(rep(0, 700), rep(1, 100), rep(2, 100),
                              rep(3, 70), rep(4, 30)),
                   division = sample(c(' A ', ' B ', ' C '), 100, replace = TRUE ),
                   exam = c(runif(700, 60, 90), runif(100, 65, 95),
                            runif(200, 75, 95)))

#view first six rows of dataset
head(data)

  offers division exam
1 0 A 66.22635
2 0 C 66.85974
3 0 A 77.87136
4 0 B 77.24617
5 0 A 62.31193
6 0 C 61.06622

Passo 2: Adattare un modello di regressione di Poisson e un modello di regressione binomiale negativa

Il codice seguente mostra come adattare ai dati sia un modello di regressione di Poisson che un modello di regressione binomiale negativa:

 #fit Poisson regression model
p_model <- glm(offers ~ division + exam, family = ' fish ', data = data)

#fit negative binomial regression model
library (MASS)

nb_model <- glm. nb (offers ~ division + exam, data = data)

Passaggio 3: creare grafici residui

Il codice seguente mostra come produrre grafici residui per entrambi i modelli.

 #Residual plot for Poisson regression
p_res <- resid (p_model)
plot(fitted(p_model), p_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Poisson ')
abline(0,0)

#Residual plot for negative binomial regression
nb_res <- resid (nb_model)
plot(fitted(nb_model), nb_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Negative Binomial ')
abline(0,0) 

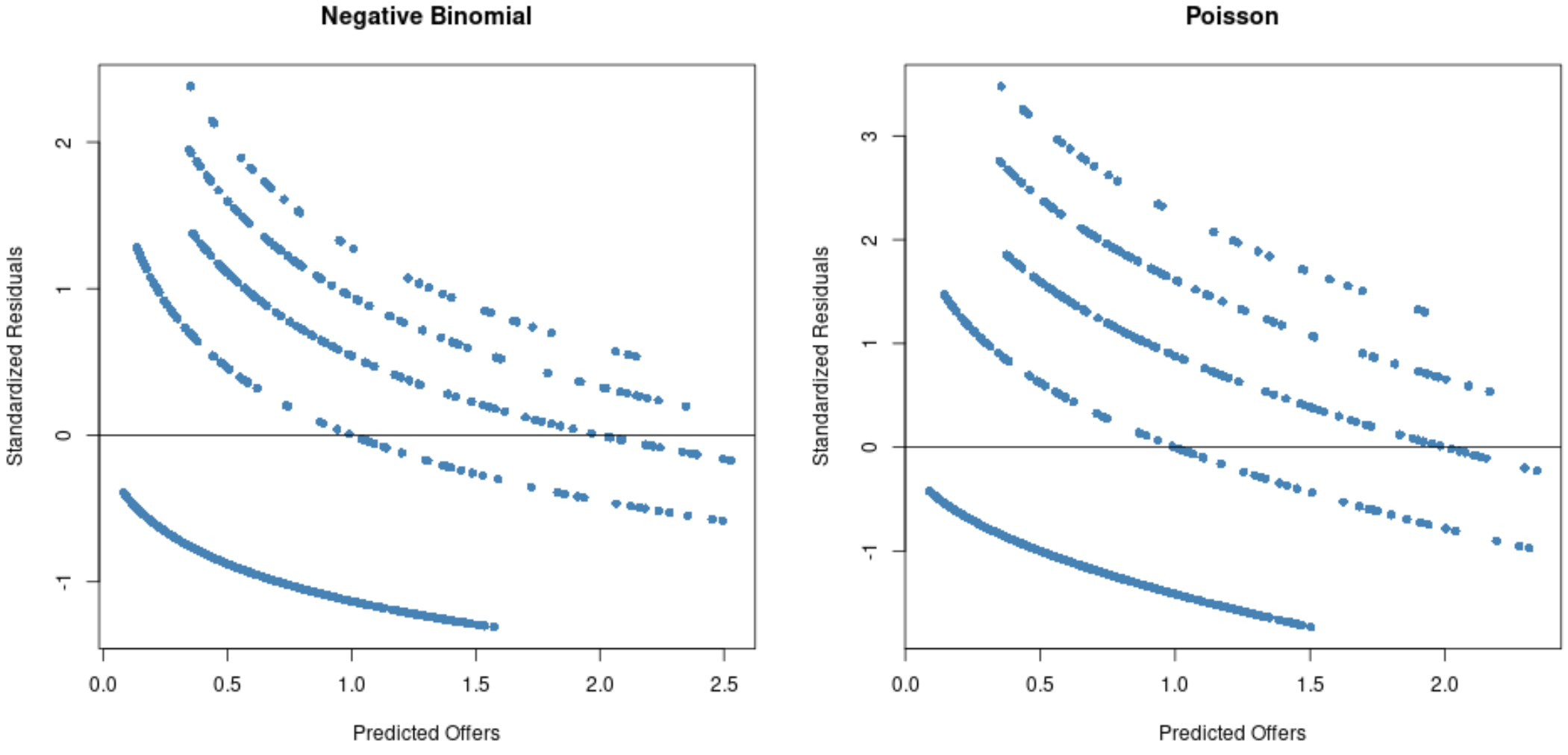
Dai grafici, possiamo vedere che i residui sono maggiormente distribuiti per il modello di regressione di Poisson (notare che alcuni residui si estendono oltre 3) rispetto al modello di regressione binomiale negativa.

Questo è un segno che un modello di regressione binomiale negativo è probabilmente più appropriato poiché i residui di questo modello sono più piccoli.

Passaggio 4: eseguire un test del rapporto di verosimiglianza

Infine, possiamo eseguire un test del rapporto di verosimiglianza per determinare se esiste una differenza statisticamente significativa nell’adattamento dei due modelli di regressione:

 pchisq(2 * ( logLik (nb_model) - logLik (p_model)), df = 1, lower. tail = FALSE )

'log Lik.' 3.508072e-29 (df=5)

Il valore p del test risulta essere 3.508072e-29 , che è significativamente inferiore a 0,05.

Pertanto, concluderemmo che il modello di regressione binomiale negativa fornisce un adattamento significativamente migliore ai dati rispetto al modello di regressione di Poisson.

Risorse addizionali

Un’introduzione alla distribuzione binomiale negativa
Un’introduzione alla distribuzione di Poisson