Come eseguire il bootstrap in r (con esempi)

Il bootstrap è un metodo che può essere utilizzato per stimare l’errore standard di qualsiasi statistica e produrre un intervallo di confidenza per la statistica.

Il processo di base per il bootstrap è il seguente:

• Prendi k campioni replicati con sostituzione da un dato set di dati.
• Per ciascun campione, calcolare la statistica di interesse.
• Ciò fornisce k stime diverse per una determinata statistica, che puoi quindi utilizzare per calcolare l’errore standard della statistica e creare un intervallo di confidenza per la statistica.

Possiamo eseguire il bootstrap in R utilizzando le seguenti funzioni dalla libreria bootstrap :

1. Genera campioni bootstrap.

boot(dati, statistiche, R, …)

Oro:

• dati: un vettore, una matrice o un blocco di dati
• statistica: una funzione che produce la/e statistica/e da avviare
• A: Numero di ripetizioni di bootstrap

2. Generare un intervallo di confidenza bootstrap.

boot.ci(oggetto di avvio, conf, tipo)

Oro:

• bootobject: un oggetto restituito dalla funzione boot()
• conf: l’intervallo di confidenza da calcolare. Il valore predefinito è 0,95
• type: tipo di intervallo di confidenza da calcolare. Le opzioni includono ‘standard’, ‘basic’, ‘stud’, ‘perc’, ‘bca’ e ‘all’ – il valore predefinito è ‘all’

I seguenti esempi mostrano come utilizzare queste funzioni nella pratica.

Esempio 1: bootstrap di una singola statistica

Il codice seguente mostra come calcolare l’errore standard per l’ R quadrato di un modello di regressione lineare semplice:

 set.seed(0)
library (boot)

#define function to calculate R-squared
rsq_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (summary(fit)$r.square) #return R-squared of model
}
#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=rsq_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = rsq_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
     original bias std. error
t1* 0.7183433 0.002164339 0.06513426

Dai risultati possiamo vedere:

• L’R quadrato stimato per questo modello di regressione è 0,7183433 .
• L’errore standard per questa stima è 0,06513426 .

Possiamo anche visualizzare rapidamente la distribuzione dei campioni sottoposti a bootstrap:

 plot(reps)

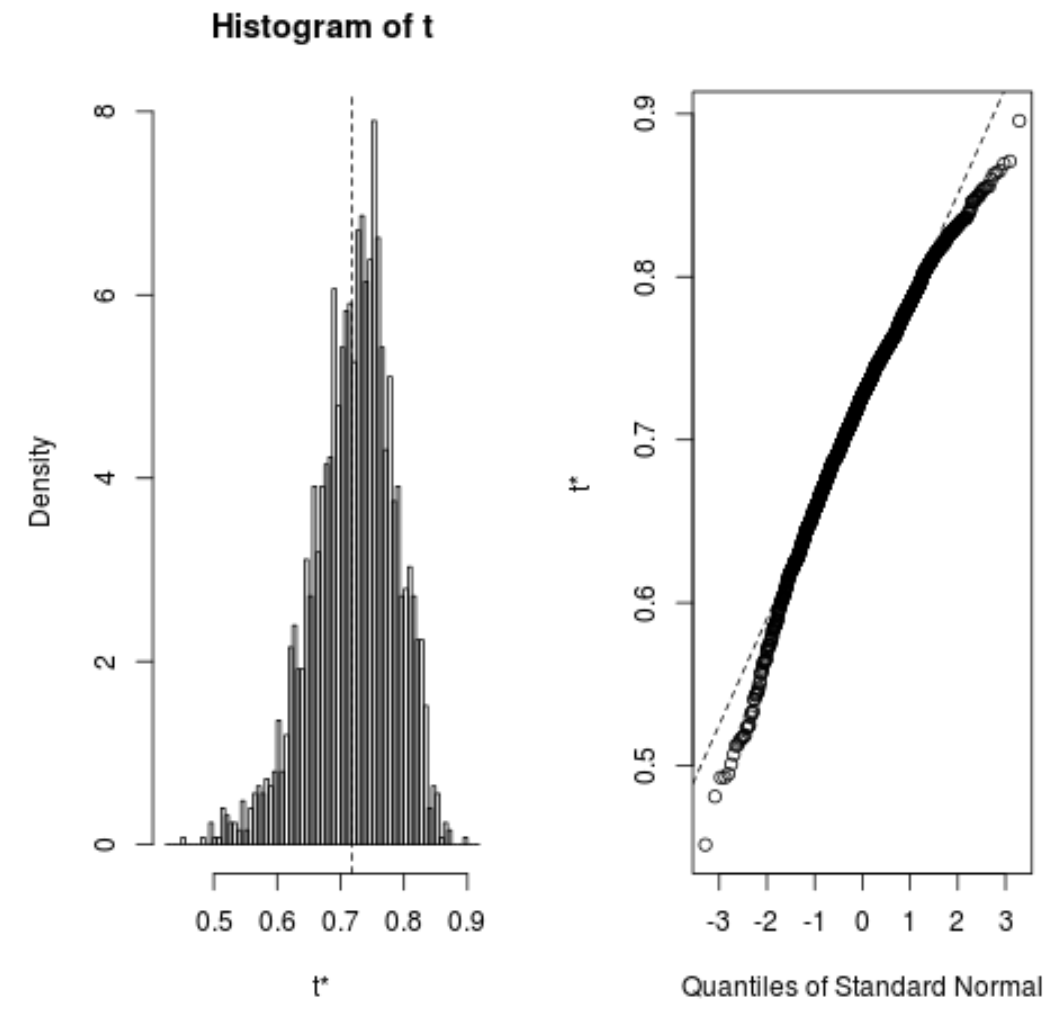
Possiamo anche utilizzare il seguente codice per calcolare l’intervallo di confidenza al 95% per l’R quadrato stimato del modello:

 #calculate adjusted bootstrap percentile (BCa) interval
boot.ci(reps, type=" bca ")

CALL: 
boot.ci(boot.out = reps, type = "bca")

Intervals: 
Level BCa          
95% (0.5350, 0.8188)  
Calculations and Intervals on Original Scale

Dal risultato, possiamo vedere che l’intervallo di confidenza bootstrap al 95% per i valori R quadrati reali è (0,5350, 0,8188).

Esempio 2: bootstrap di più statistiche

Il codice seguente mostra come calcolare l’errore standard per ciascun coefficiente in un modello di regressione lineare multipla:

 set.seed(0)
library (boot)

#define function to calculate fitted regression coefficients
coef_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (coef(fit)) #return coefficient estimates of model
}

#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=coef_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = coef_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
       original bias std. error
t1* 29.59985476 -5.058601e-02 1.49354577
t2* -0.04121512 6.549384e-05 0.00527082

Dai risultati possiamo vedere:

• Il coefficiente stimato per l’intercetta del modello è 29,59985476 e l’errore standard di questa stima è 1,49354577 .
• Il coefficiente stimato per la variabile predittiva disp nel modello è -0,04121512 e l’errore standard di questa stima è 0,00527082 .

Possiamo anche visualizzare rapidamente la distribuzione dei campioni sottoposti a bootstrap:

 plot(reps, index=1) #intercept of model
plot(reps, index=2) #disp predictor variable

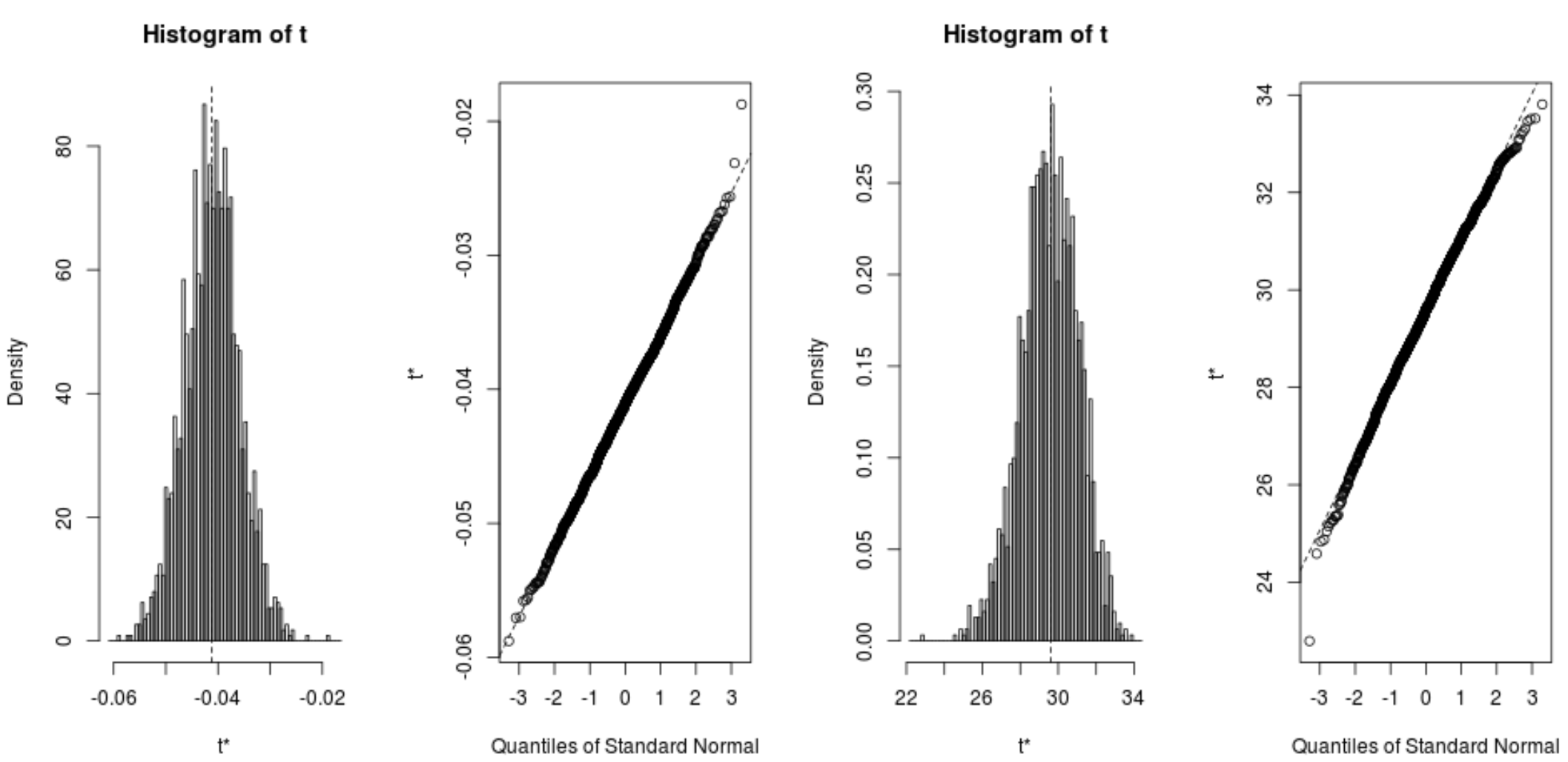
Possiamo anche utilizzare il seguente codice per calcolare gli intervalli di confidenza al 95% per ciascun coefficiente:

 #calculate adjusted bootstrap percentile (BCa) intervals
boot.ci(reps, type=" bca ", index=1) #intercept of model
boot.ci(reps, type=" bca ", index=2) #disp predictor variable

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 1)

Intervals: 
Level BCa          
95% (26.78, 32.66)  
Calculations and Intervals on Original Scale
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 2000 bootstrap replicates

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 2)

Intervals: 
Level BCa          
95% (-0.0520, -0.0312)  
Calculations and Intervals on Original Scale

Dai risultati, possiamo vedere che gli intervalli di confidenza bootstrap al 95% per i coefficienti del modello sono i seguenti:

• IC per intercettazione: (26.78, 32.66)
• CI per visualizzazione : (-.0520, -.0312)

Risorse addizionali

Come eseguire una regressione lineare semplice in R
Come eseguire la regressione lineare multipla in R
Introduzione agli intervalli di confidenza