Diagramma della scatola e dei baffi

Questo articolo spiega cos’è un boxplot, noto anche come boxplot (o boxplot). Scoprirai come sono realizzati questi tipi di diagrammi statistici e un esercizio risolto di un diagramma a scatola e baffi e la sua interpretazione.

Che cos’è il diagramma a scatola e baffi?

Il boxplot , chiamato anche boxplot o boxplot , è un grafico che rappresenta visivamente un insieme di dati statistici utilizzando quartili.

La caratteristica principale del box and whisker plot è che permette di visualizzare rapidamente la dispersione di una serie di dati, poiché indica i quartili, la mediana, i valori estremi e gli outlier dei dati.

Pertanto, questo tipo di diagramma è composto da una scatola rettangolare e da alcune linee (o baffi) da cui emergono i seguenti valori:

• I confini del riquadro indicano il primo e il terzo quartile (Q ₁ e Q ₃ ). E la linea verticale all’interno della scatola è la mediana (equivalente al secondo quartile _Q2 ).
• I limiti dei baffi (o delle braccia) sono i valori estremi , cioè il valore minimo e il valore massimo della serie di dati.
• I punti fuori dai baffi sono valori anomali , ovvero dati che probabilmente sono stati misurati in modo errato e che quindi non dovrebbero essere presi in considerazione nello studio statistico.

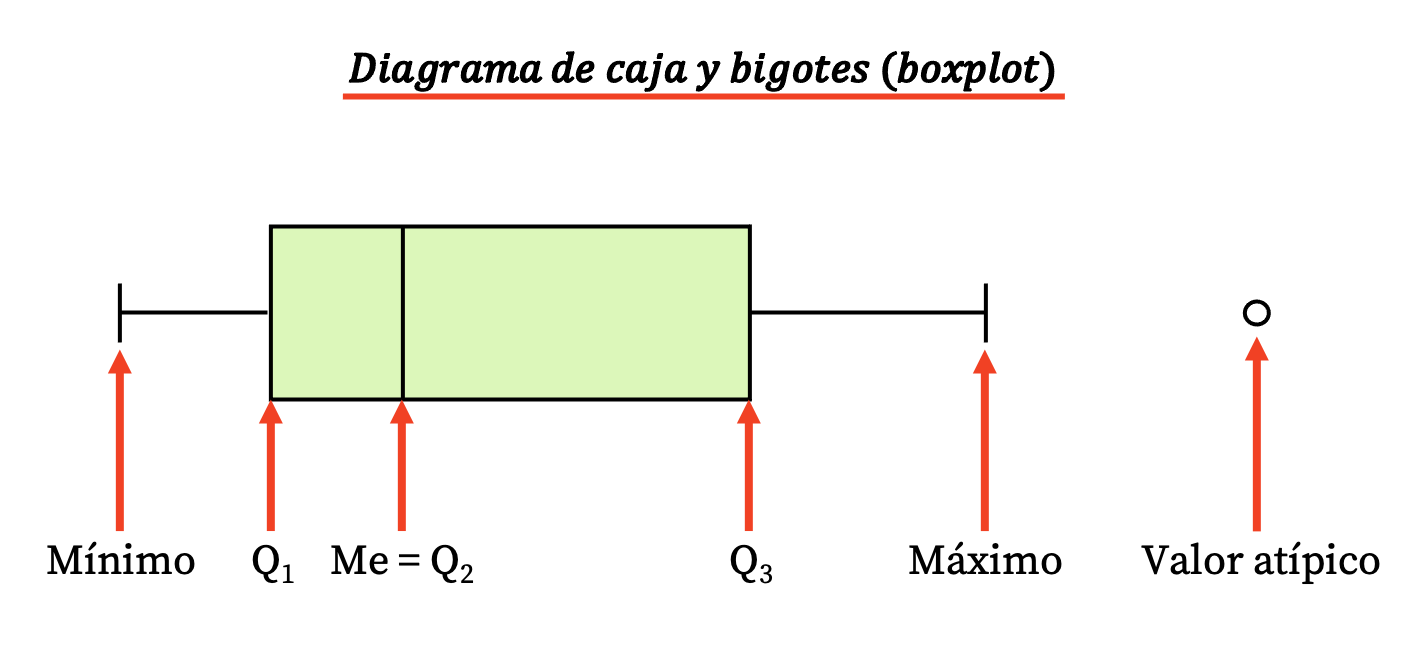
Si noti che la differenza tra il terzo e il primo quartile è l’intervallo interquartile (o intervallo interquartile), un’altra misura della dispersione statistica.

I grafici a scatola e a baffi sono molto utili per confrontare variabili numeriche. Tuttavia, non è adatto per rappresentare variabili categoriali.

Come creare un grafico a scatola e baffi

Per creare un diagramma a scatola e baffi (o diagramma a scatola) da una serie di dati, è necessario eseguire i seguenti passaggi:

1. Ordinare gli esempi di dati statistici.
2. Calcola i quartili (Q ₁ , Q ₂ e Q ₃ ) e rappresentali come il riquadro nel diagramma. Il primo e il terzo quartile corrispondono ai limiti della casella, e per rappresentare la mediana (il secondo quartile) bisogna tracciare una linea all’interno della casella dove si trova il suo valore.
3. Calcolare l’intervallo interquartile, che è uguale al terzo quartile meno il primo quartile.



4. Calcolare i valori ammissibili LI e LS, le cui formule sono:





5. Identificare i valori anomali del campione, che sono valori inferiori a LI o superiori a LS. Rappresenta questi valori al di fuori dell’intervallo dei baffi con punti.
6. Identificare e rappresentare i valori estremi, ovvero il valore più piccolo e il valore più grande nell’intervallo formato da LI e LS. Questi valori rappresentano la fine dei due baffi nel diagramma.

Esempio di grafico Box e Whisker

Considerando la definizione e la teoria del box and whisker plot (o boxplot), troverete di seguito un esempio concreto per comprendere meglio il concetto e vedere come si realizza questo tipo di grafico statistico.

• Disegna un boxplot del seguente set di dati statistici.

In questo caso i dati sono già ordinati dal più piccolo al più grande, quindi non sono necessarie modifiche. Altrimenti, dovremmo prima ordinare i dati del campione.

Successivamente estraiamo i quartili del campione:

Una volta calcolati i tre quartili, troviamo lo scarto interquartile sottraendo il quartile 3 meno il quartile 1:

Calcoliamo ora i limiti LI e LS, che sono i valori a partire dai quali i dati sono considerati atipici. Per fare ciò, è necessario utilizzare le seguenti formule:

Quindi in questo caso abbiamo due valori anomali, perché 3,02 è inferiore a 3,16 e 5,71 è maggiore di 5,56.

Resta infine da individuare i valori estremi, che sono il minimo ed il massimo di tutti i dati che si trovano nell’intervallo [LI,LS]. Pertanto, nel nostro esempio, il valore minimo è 3,70 e il valore massimo è 4,81.

Quindi, una volta individuati tutti i valori del box e del baffo, non resta che realizzare la rappresentazione grafica:

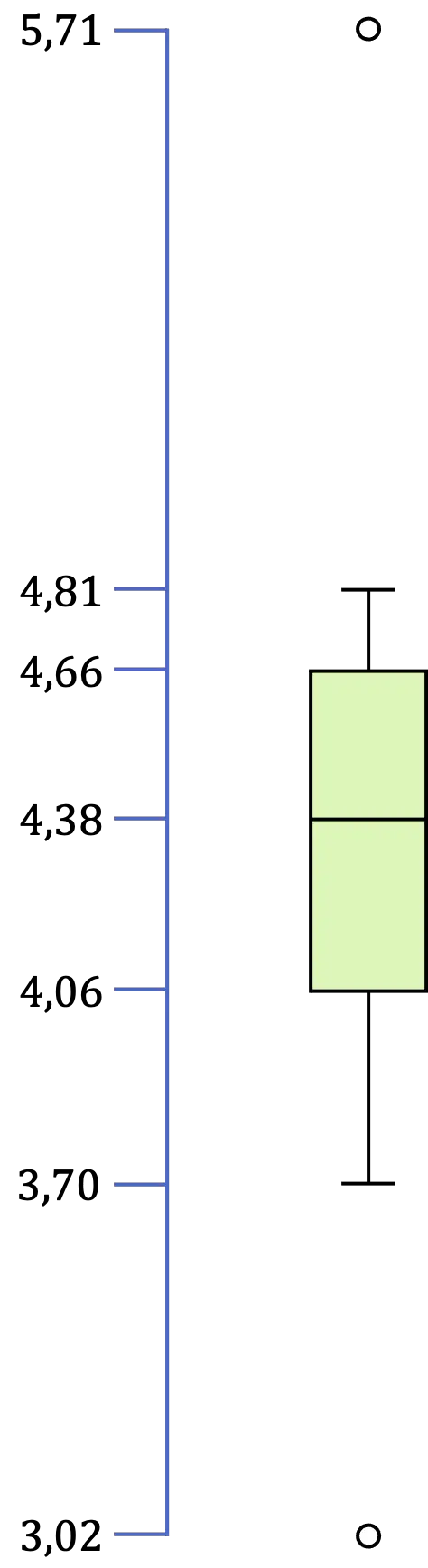
A cosa serve il diagramma a scatola e baffi?

Infine, vediamo a cosa serve e come interpretare il box and whisker plot (o boxplot).

Ovviamente, il box and whisker plot è molto utile per conoscere rapidamente i quartili, lo scarto interquartile, la mediana, i valori estremi e gli outlier di una serie di dati, poiché tutte queste misure statistiche possono essere identificate con un semplice see.

Inoltre, il diagramma a scatola e baffi viene utilizzato per analizzare la simmetria del campione statistico, poiché rappresenta visivamente l’intero set di dati. Se la mediana non è al centro del riquadro, significa che il campione non è simmetrico.

Allo stesso modo, i boxplot sono ampiamente utilizzati nel mercato azionario per rappresentare la variazione del prezzo di un titolo in un periodo di tempo, poiché consentono di vedere il valore massimo, il valore minimo e i valori intermedi in un breve periodo di tempo. tempo e quindi prendere decisioni più rapide.