Come calcolare i valori p in excel (3 esempi)

In statistica, utilizziamo il test di ipotesi per determinare se un’affermazione su un parametro della popolazione è vera o meno.

Quando eseguiamo un test di ipotesi, spesso ci viene fornita una statistica del test T-score.

Una volta trovata questa statistica del test t-score, possiamo trovare il valore p ad essa associato.

Se questo valore p è inferiore a un certo valore (ad esempio 0,10, 0,05, 0,01), allora rifiutiamo l’ipotesi nulla del test e concludiamo che i nostri risultati sono statisticamente significativi.

Gli esempi seguenti mostrano come calcolare un valore p per una statistica di test in Excel in tre diversi scenari.

Esempio 1: calcolare il valore P per un test a due code

Supponiamo che un botanico voglia sapere se l’altezza media di una certa specie di pianta è pari a 15 pollici.

In un campione casuale di 12 piante, scopre che l’altezza media del campione è di 14,33 pollici e la deviazione standard del campione è di 1,37 pollici.

Esegue un test di ipotesi utilizzando le seguenti ipotesi nulle e alternative:

H ₀ (ipotesi nulla): μ= 15 pollici

H _A (ipotesi alternativa): μ ≠ 15 pollici

La statistica del test viene calcolata come segue:

• t = ( X – µ) / (s/ √n )
• t = (14,33-15) / (1,37/√ 12 )
• t = -1.694

I gradi di libertà associati a questa statistica del test sono n-1 = 12-1 = 11 .

Per trovare il valore p per questa statistica del test, utilizzeremo la seguente formula in Excel:

 =T.DIST.2T(ABS(-1.694), 11)

Lo screenshot seguente mostra come utilizzare questa formula nella pratica.

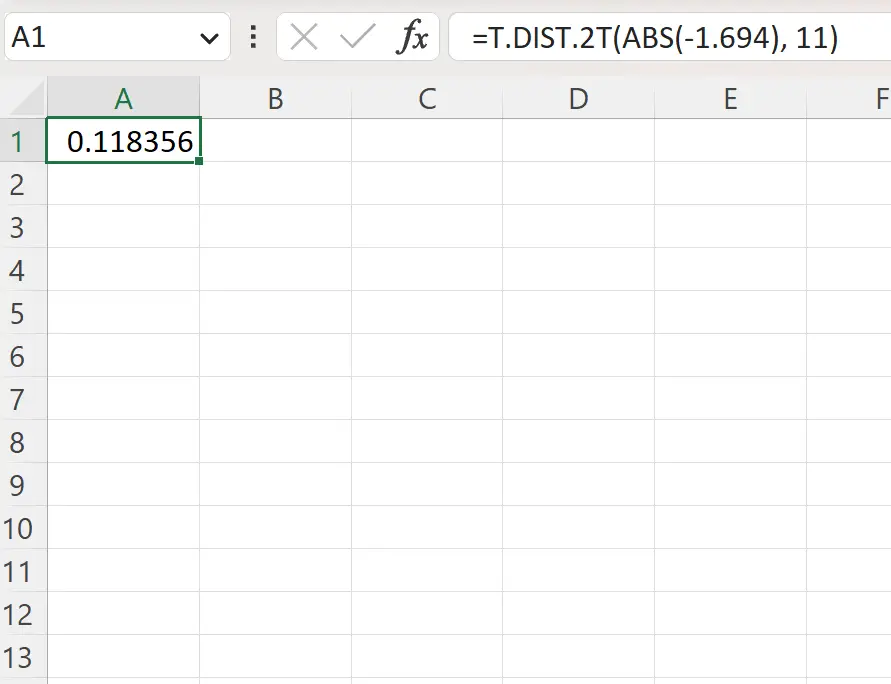
Il valore p a due code è 0,1184 .

Poiché questo valore non è inferiore a 0,05, non si rifiuta l’ipotesi nulla. Non abbiamo prove sufficienti per affermare che l’altezza media delle piante sia diversa da 15 pollici.

Esempio 2: calcolare il valore P per il test a sinistra

Supponiamo di assumere che il peso medio di un determinato gadget prodotto in una fabbrica sia di 20 grammi. Tuttavia, un ispettore stima che il peso medio effettivo sia inferiore a 20 grammi.

Per testarlo, pesa un semplice campione casuale di 20 widget e ottiene le seguenti informazioni:

• n = 20 widget
• x = 19,8 grammi
• s = 3,1 grammi

Quindi esegue un test di ipotesi utilizzando le seguenti ipotesi nulle e alternative:

H ₀ (ipotesi nulla): μ ≥ 20 grammi

H _A (ipotesi alternativa): μ < 20 grammi

La statistica del test viene calcolata come segue:

• t = ( X – µ) / (s/ √n )
• t = (19,8-20) / (3,1/√ 20 )
• t = -.2885

I gradi di libertà associati a questa statistica del test sono n-1 = 20-1 = 19 .

Per trovare il valore p per questa statistica del test, utilizzeremo la seguente formula in Excel:

 =T.DIST(-.2885, 19, TRUE)

Lo screenshot seguente mostra come utilizzare questa formula nella pratica.

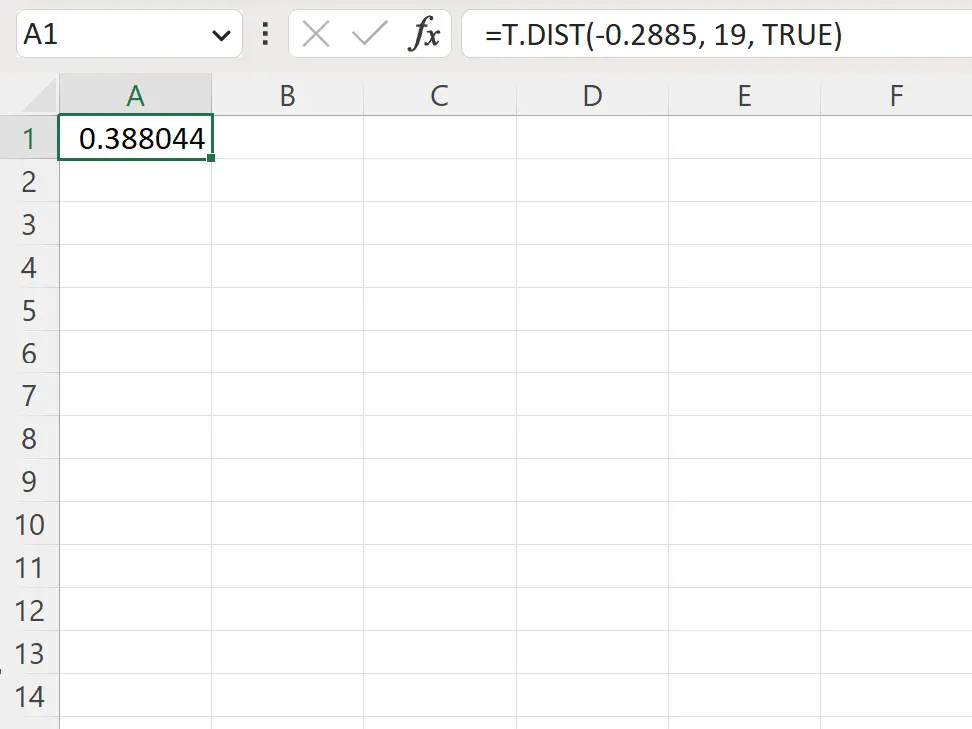
Il valore p a sinistra è 0,388044 .

Poiché questo valore non è inferiore a 0,05, l’ispettore non riesce a rifiutare l’ipotesi nulla. Non ci sono prove sufficienti per affermare che il peso medio effettivo dei widget prodotti in questa fabbrica sia inferiore a 20 grammi.

Nota : abbiamo utilizzato l’argomento VERO per specificare che la funzione di distribuzione cumulativa deve essere utilizzata quando si calcola il valore p.

Esempio 3: calcolare il valore P per il test della coda di destra

Supponiamo che l’altezza media di una determinata specie di piante sia di 10 pollici. Tuttavia, un botanico afferma che la vera altezza media è superiore a 10 pollici.

Per verificare questa affermazione, misura l’altezza di un campione casuale semplice di 15 piante e ottiene le seguenti informazioni:

• n = 15 piante
• x = 11,4 pollici
• s = 2,5 pollici

Quindi esegue un test di ipotesi utilizzando le seguenti ipotesi nulle e alternative:

H ₀ (ipotesi nulla): μ ≤ 10 pollici

H _A (ipotesi alternativa): μ > 10 pollici

La statistica del test viene calcolata come segue:

• t = ( X – µ) / (s/ √n )
• t = (11,4-10) / (2,5/√ 15 )
• t = 2,1689

I gradi di libertà associati a questa statistica del test sono n-1 = 15-1 = 14 .

Per trovare il valore p per questa statistica del test, utilizzeremo la seguente formula in Excel:

 =T.DIST.RT(2.1689, 14)

Lo screenshot seguente mostra come utilizzare questa formula nella pratica.

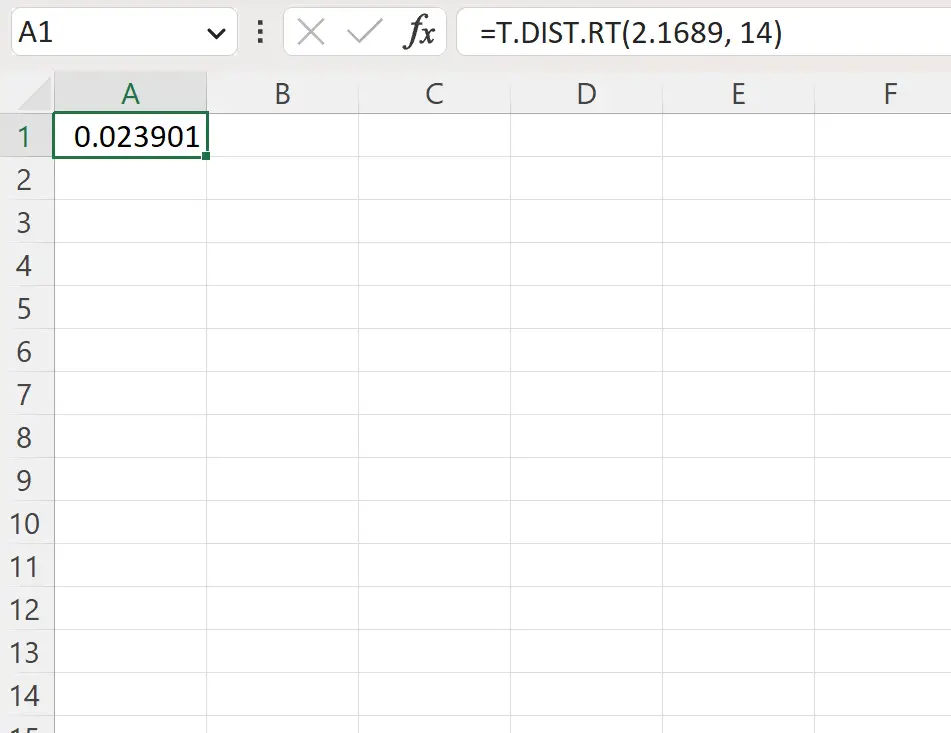
Il valore p a destra è 0,023901 .

Essendo questo valore inferiore a 0,05, il botanico può rifiutare l’ipotesi nulla. Ha prove sufficienti per affermare che la vera altezza media di questa specie di pianta è di oltre 10 pollici.

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in Excel:

Come trovare un valore P da un punteggio Z in Excel
Come trovare il valore P di una statistica F in Excel
Come trovare il valore P di una statistica chi-quadrato in Excel