Come calcolare un coefficiente di correlazione su una calcolatrice ti-84
Un coefficiente di correlazione è una misura dell’associazione lineare tra due variabili. Può assumere un valore compreso tra -1 e 1 dove:
- -1 indica una correlazione lineare perfettamente negativa tra due variabili
- 0 indica alcuna correlazione lineare tra due variabili
- 1 indica una correlazione lineare perfettamente positiva tra due variabili
È possibile utilizzare i seguenti passaggi per calcolare il coefficiente di correlazione tra due variabili su una calcolatrice TI-84:
Passaggio 1: abilitare la diagnostica.
Innanzitutto, dobbiamo abilitare la diagnostica. Per fare ciò, premere 2nd quindi premere il numero 0. Questo ci porterà alla schermata CATALOGO.

Scorrere fino a DiagnosticOn e premere INVIO .
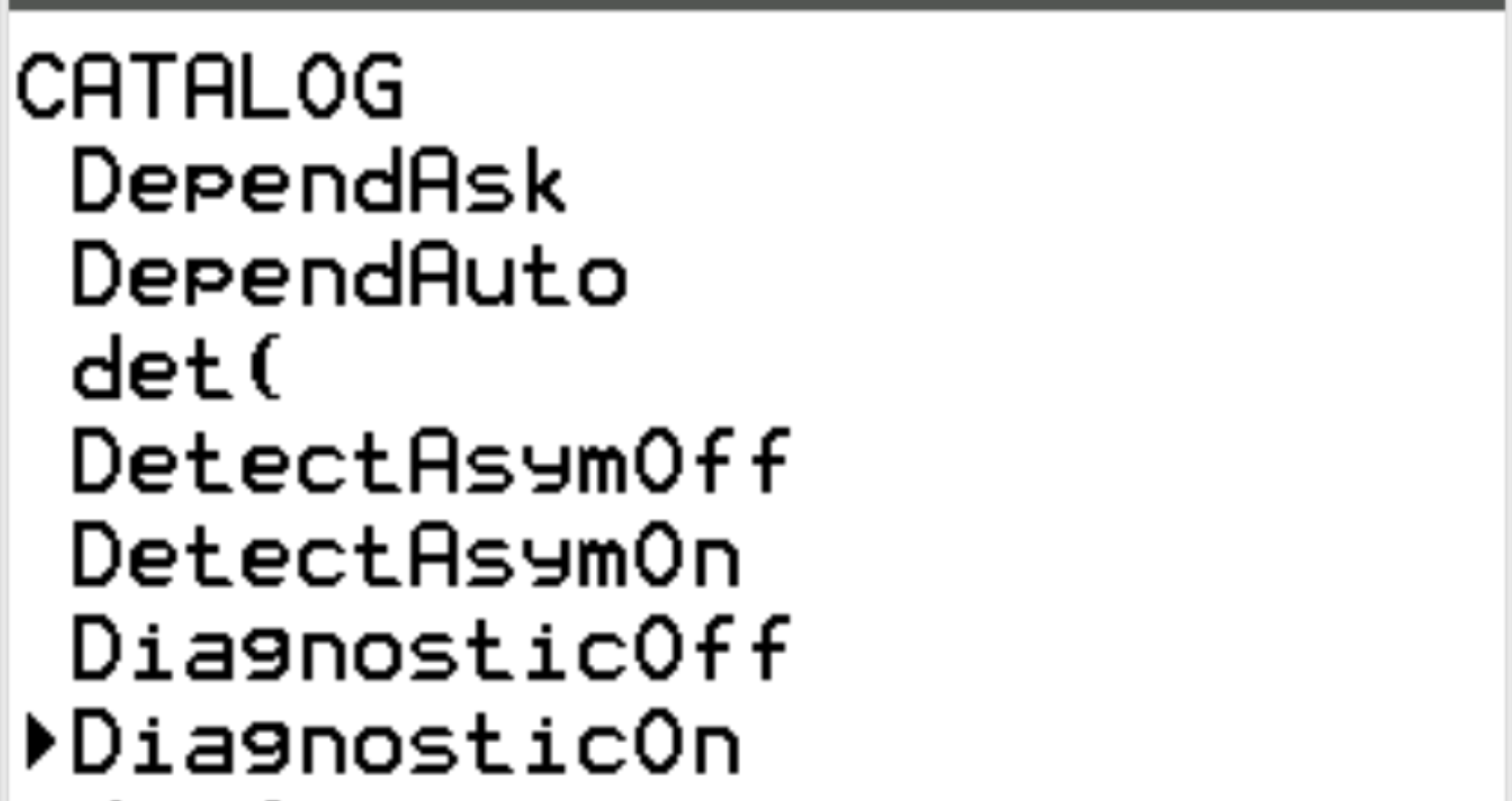
Quindi premere nuovamente INVIO .
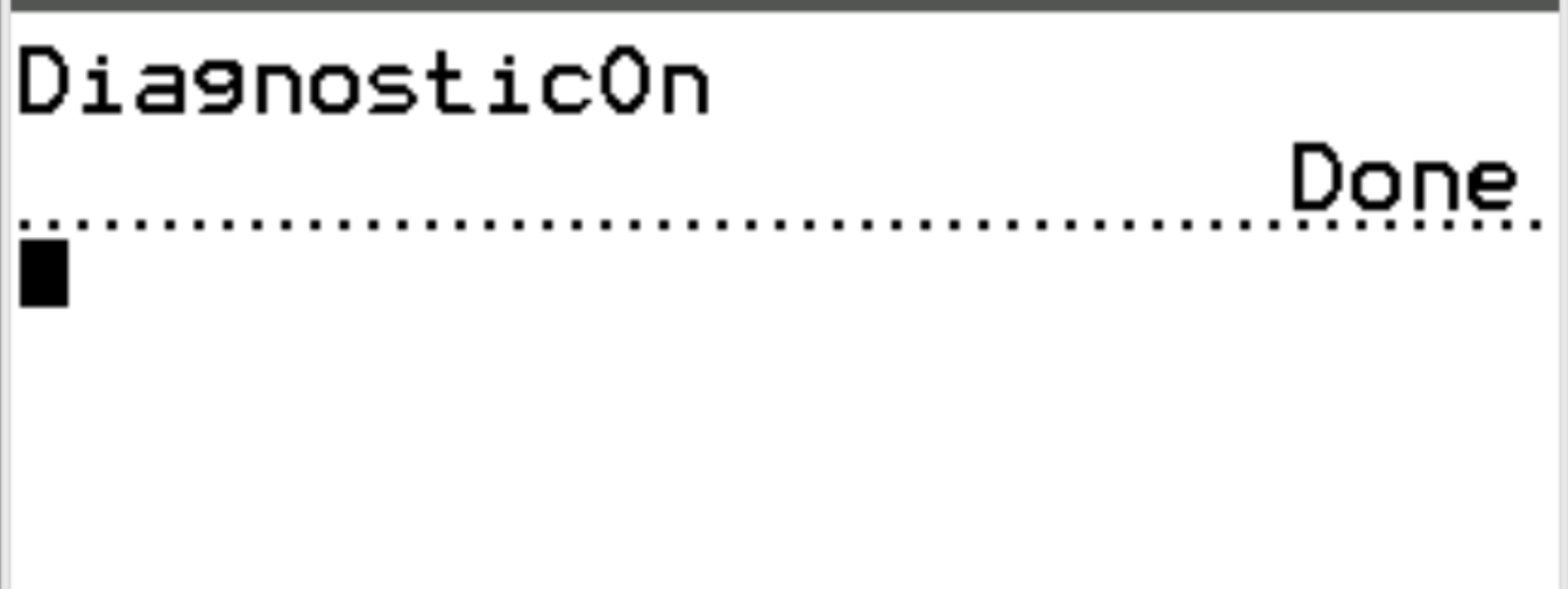
La diagnostica è ora abilitata in modo da poter calcolare il coefficiente di correlazione tra due variabili.
Passaggio 2: inserisci i dati.
Successivamente, dobbiamo inserire i valori dei dati per le nostre due variabili. Premere Stat quindi premere EDIT . Inserisci i valori della prima variabile nella colonna L1 e i valori della seconda variabile nella colonna L2:
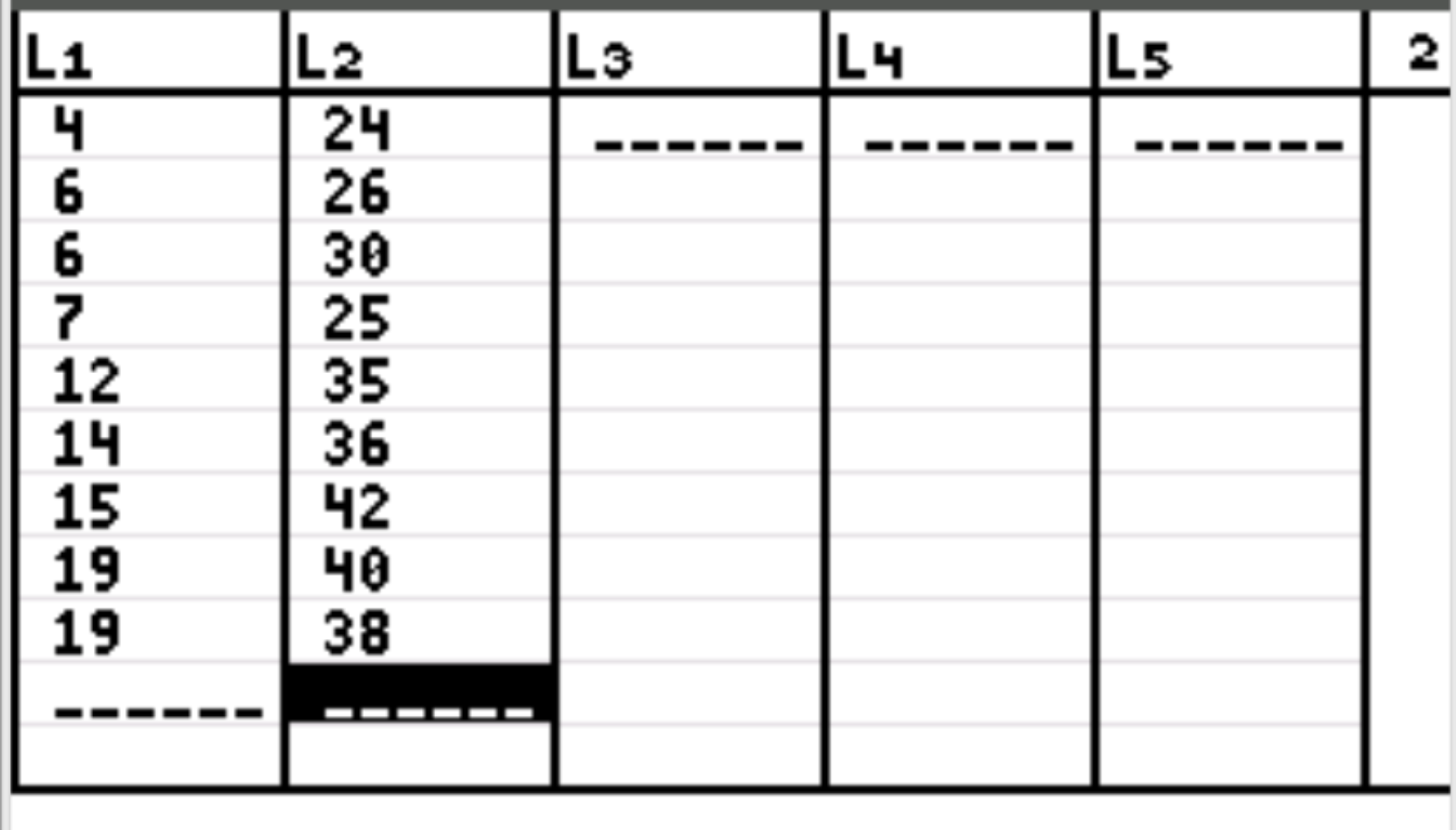
Passaggio 3: trovare il coefficiente di correlazione.
Successivamente, calcoleremo il coefficiente di correlazione tra le due variabili. Premere Stat quindi scorrere fino a CALC . Quindi scorrere fino a 8: Linreg(a+bx) e premere Invio .
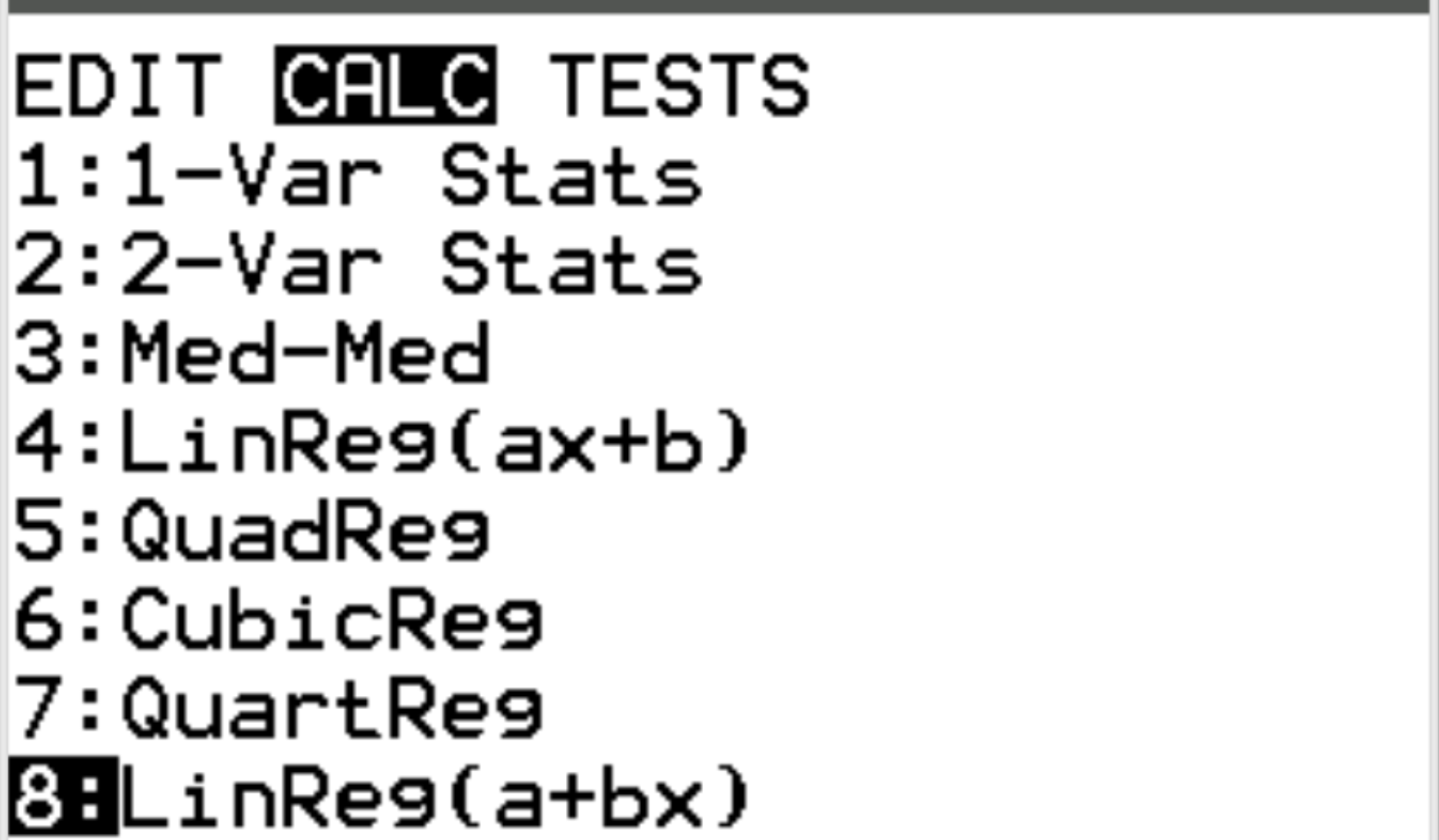
Per Xlist e Ylist, assicurati che L1 e L2 siano selezionati poiché queste sono le colonne che abbiamo utilizzato per inserire i nostri dati. Lascia FreqList vuoto. Scorri verso il basso fino a Calcola e premi Invio .
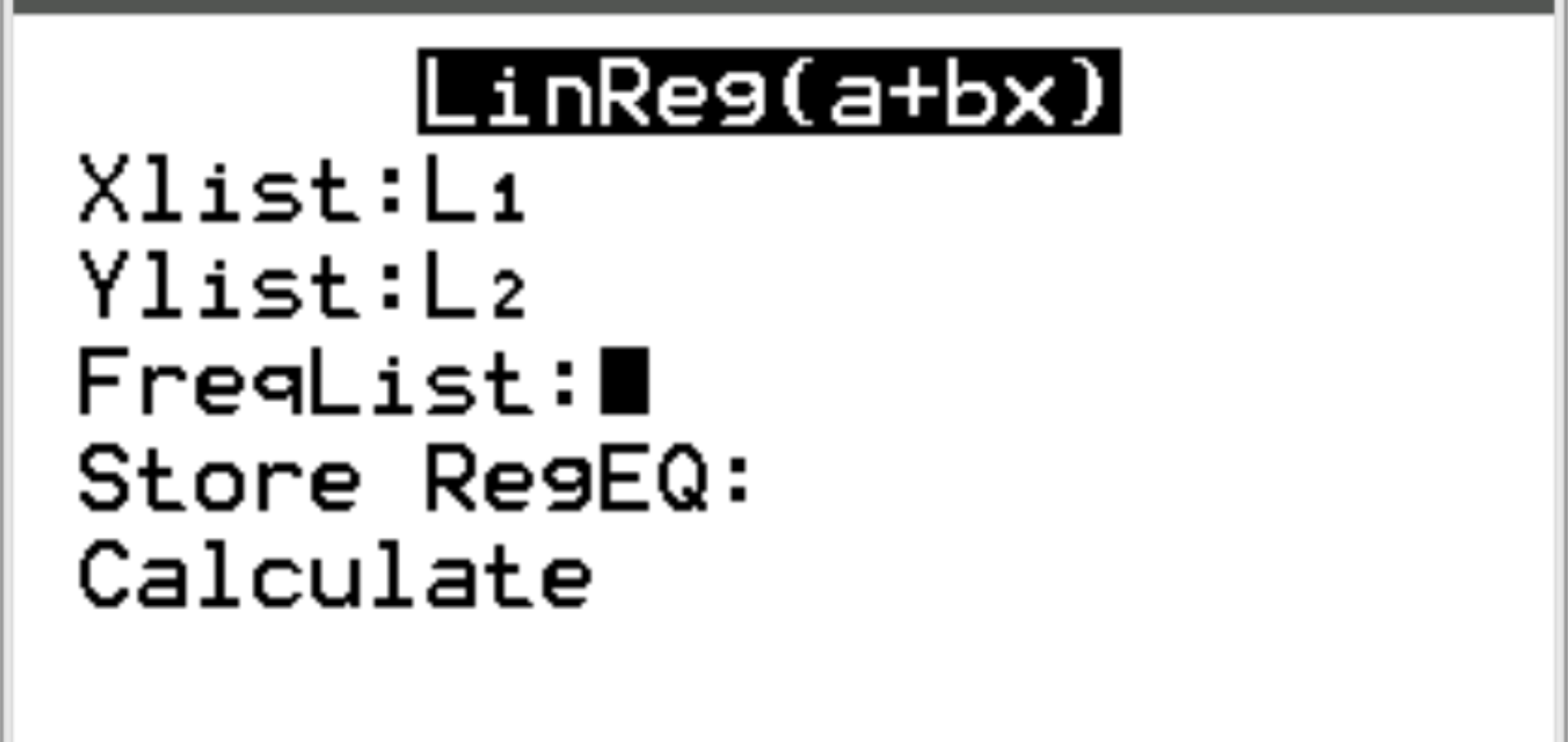
Nella nuova schermata possiamo vedere che il coefficiente di correlazione (r) tra le due variabili è 0,9145 .
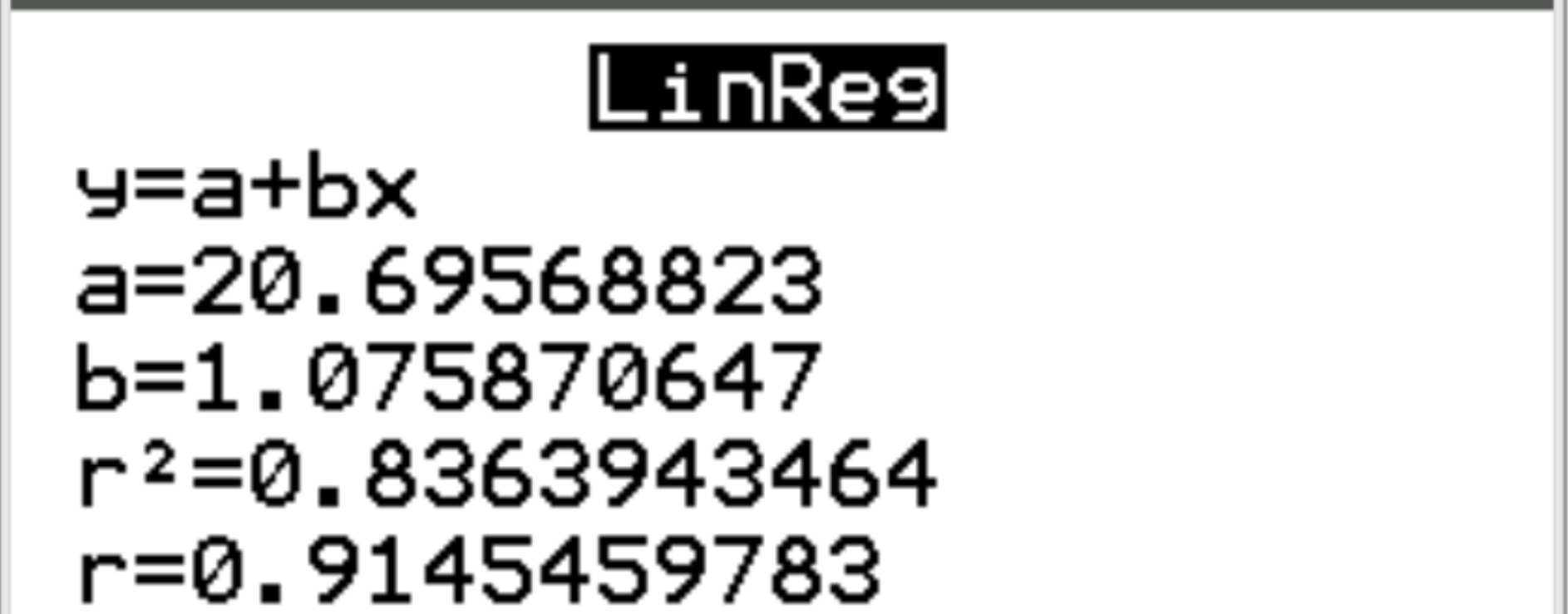
Come interpretare un coefficiente di correlazione
La tabella seguente mostra la regola pratica per interpretare la forza della relazione tra due variabili in base al valore di r :
| Valore assoluto di r | Forza della relazione |
|---|---|
| r<0,25 | Nessuna relazione |
| 0,25 < r < 0,5 | Relazione debole |
| 0,5 < r < 0,75 | Relazioni moderate |
| r > 0,75 | Relazione forte |
Nel nostro esempio, un coefficiente di correlazione di 0,9145 indica una forte relazione positiva tra le due variabili.