Come eseguire l'anova unidirezionale su una calcolatrice ti-84

Un’ANOVA unidirezionale viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi indipendenti.

Questo tutorial spiega come eseguire un’ANOVA unidirezionale su una calcolatrice TI-84.

Esempio: ANOVA unidirezionale su una calcolatrice TI-84

Supponiamo di reclutare 30 studenti per partecipare a uno studio. Agli studenti viene assegnato in modo casuale l’utilizzo di una delle tre tecniche di studio per un mese per prepararsi a un esame. Alla fine del mese tutti gli studenti sostengono lo stesso test.

Utilizzare i passaggi seguenti per eseguire un’ANOVA unidirezionale per determinare se i punteggi medi sono gli stessi nei tre gruppi.

Passaggio 1: inserisci i dati.

Innanzitutto, inseriremo i valori dei dati per la variabile esplicativa e la variabile di risposta. Premere Stat quindi premere EDIT . Inserisci i seguenti risultati dell’esame per gli studenti che hanno utilizzato la prima tecnica di studio nella colonna L1, la seconda tecnica di studio nella colonna L2 e la terza tecnica di studio nella colonna L3:

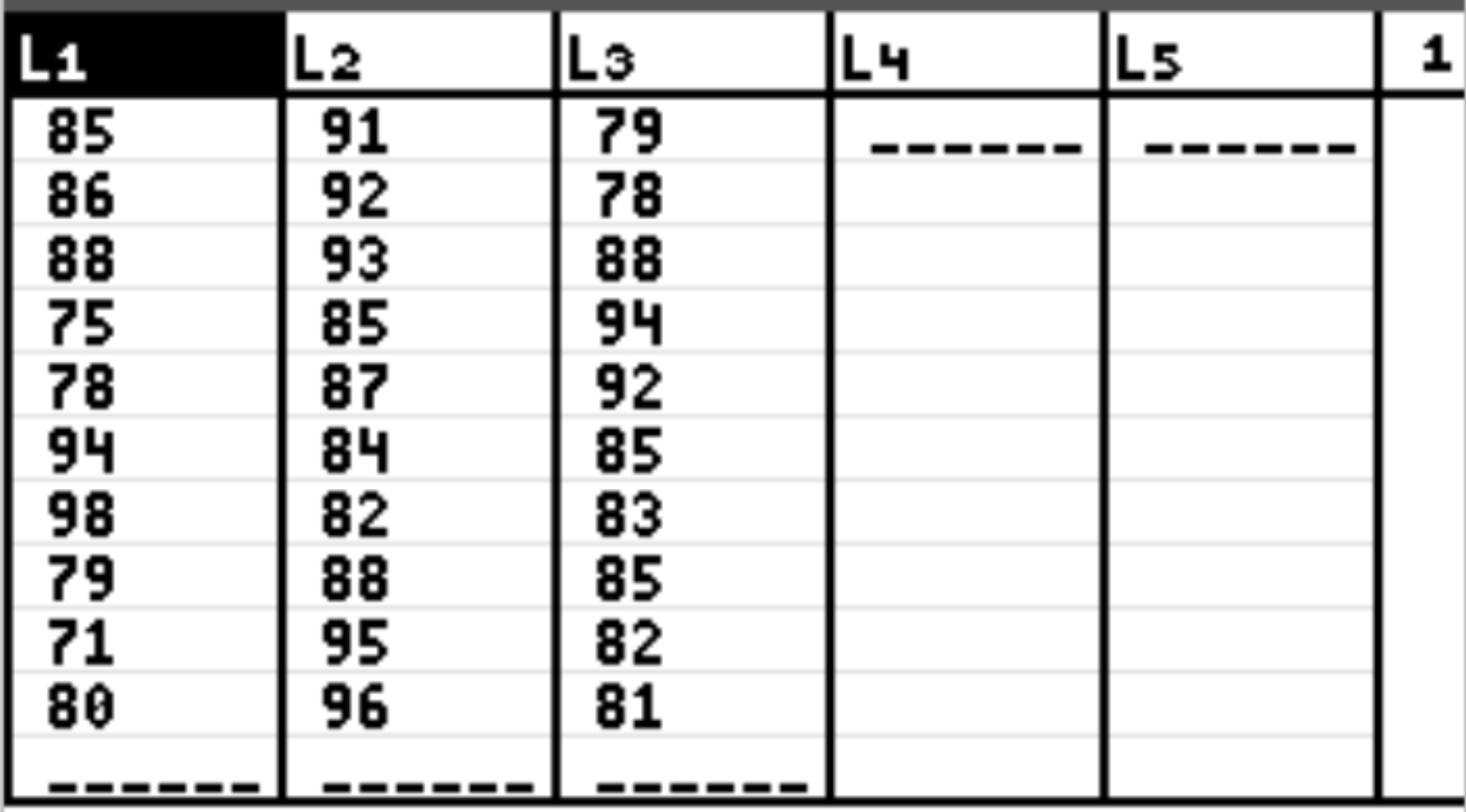
Passaggio 2: eseguire l’ANOVA unidirezionale.

Successivamente, eseguiremo l’ANOVA unidirezionale. Premere Stat quindi scorrere fino a TESTS . Quindi scorrere fino a ANOVA e premere Invio .

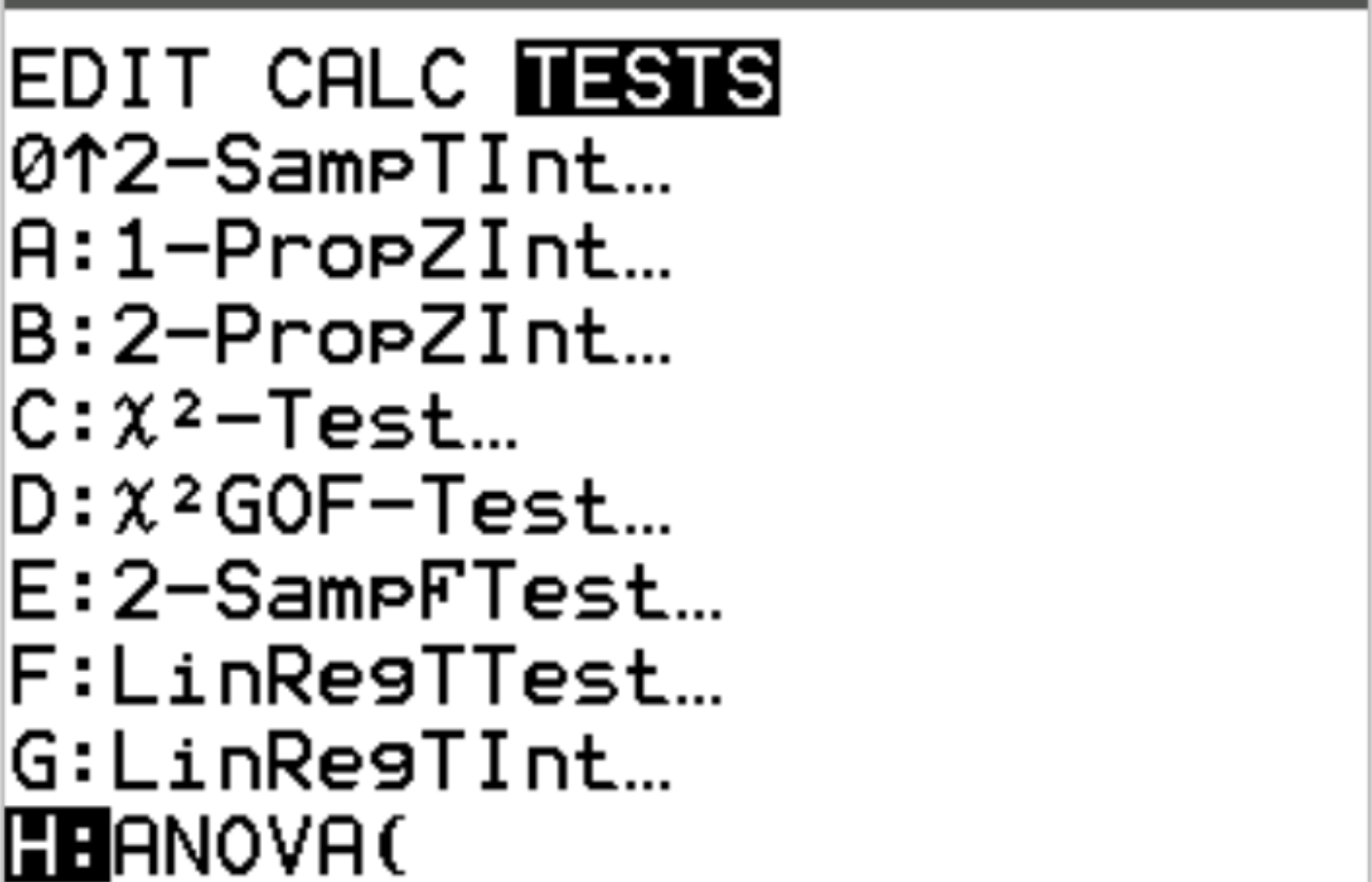
Immettere gli elenchi in cui sono archiviati i dati separati da virgole, quindi aggiungere una parentesi di chiusura ) quindi premere Invio .

Nota: per visualizzare L1, premere 2 , quindi premere 1 . Per visualizzare L2, premere 2nd quindi premere 2 . Per richiamare L3, premere 2nd quindi premere 3 .

I seguenti risultati appariranno dopo aver premuto Invio :

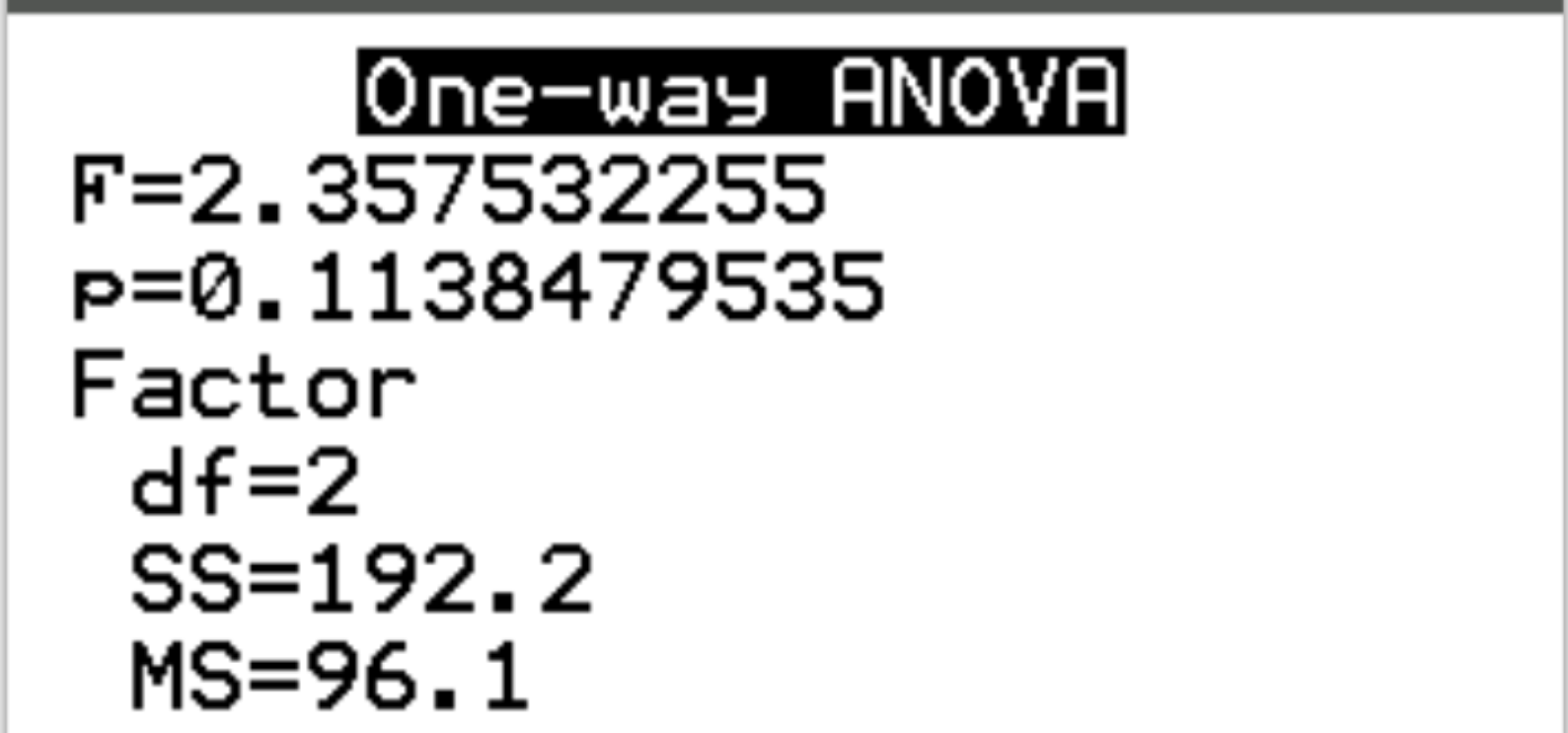
Passaggio 3: interpretare i risultati.

La statistica F del test è 2,3575 e il corrispondente valore p è 0,1138 . Poiché questo valore p non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla.

Pertanto, non abbiamo prove sufficienti per affermare che il punteggio medio dell’esame sia diverso tra i tre gruppi. In altre parole, non abbiamo prove sufficienti per affermare che la tecnica di studio porta a risultati di test diversi.