Test di indipendenza del chi quadrato su una calcolatrice ti-84
Un test di indipendenza chi quadrato viene utilizzato per determinare se esiste o meno un’associazione significativa tra due variabili categoriali.
Questo tutorial spiega come eseguire un test di indipendenza chi quadrato su una calcolatrice TI-84.
Esempio: test di indipendenza del chi quadrato su una calcolatrice TI-84
Supponiamo di voler sapere se il genere è associato o meno alla preferenza per un partito politico. Prendiamo un semplice campione casuale di 500 elettori e chiediamo loro quale sia la loro preferenza per il partito politico. La tabella seguente presenta i risultati dell’indagine:
| Repubblicano | Democratico | Indipendente | Totale | |
| Maschio | 120 | 90 | 40 | 250 |
| Femmina | 110 | 95 | 45 | 250 |
| Totale | 230 | 185 | 85 | 500 |
Utilizzare i seguenti passaggi per eseguire un test di indipendenza chi-quadrato per determinare se il genere è associato alla preferenza del partito politico.
Passaggio 1: inserisci i dati.
Innanzitutto, inseriremo i dati in una matrice. Premere 2nd quindi premere x -1 . Scorrere verso il basso fino a Modifica , evidenziare qualsiasi matrice vuota e premere Invio . Successivamente, scegli il numero di righe (2 nel nostro caso) e colonne (3 nel nostro caso) da utilizzare nella matrice e inserisci i dati grezzi:

Passaggio 2: eseguire un test di indipendenza chi quadrato.
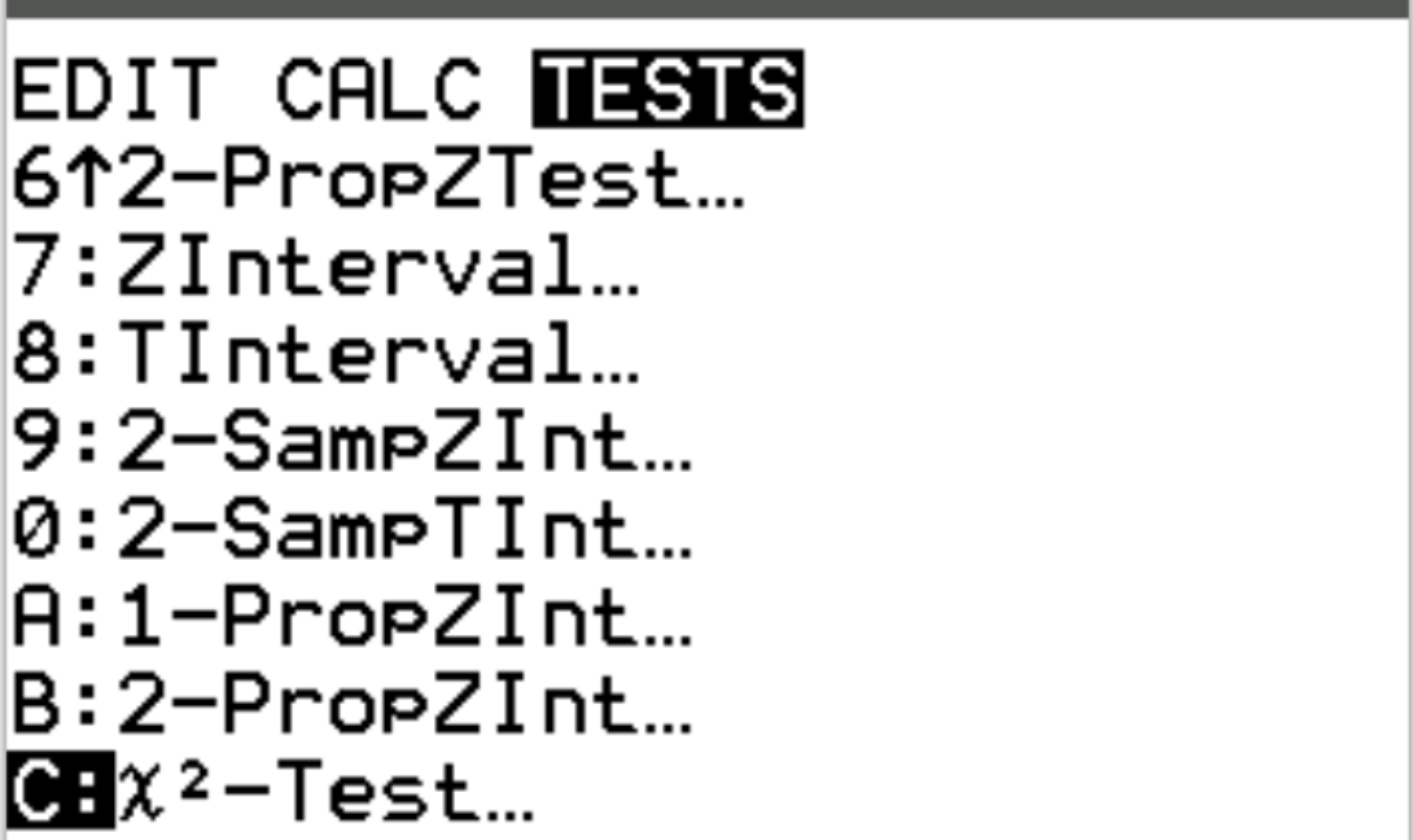
Successivamente, eseguiremo un test di indipendenza del Chi-quadrato sulla matrice che abbiamo appena creato. Premere stat e scorrere fino a TESTS . Quindi scorrere fino a X 2 -Test e premere Invio .
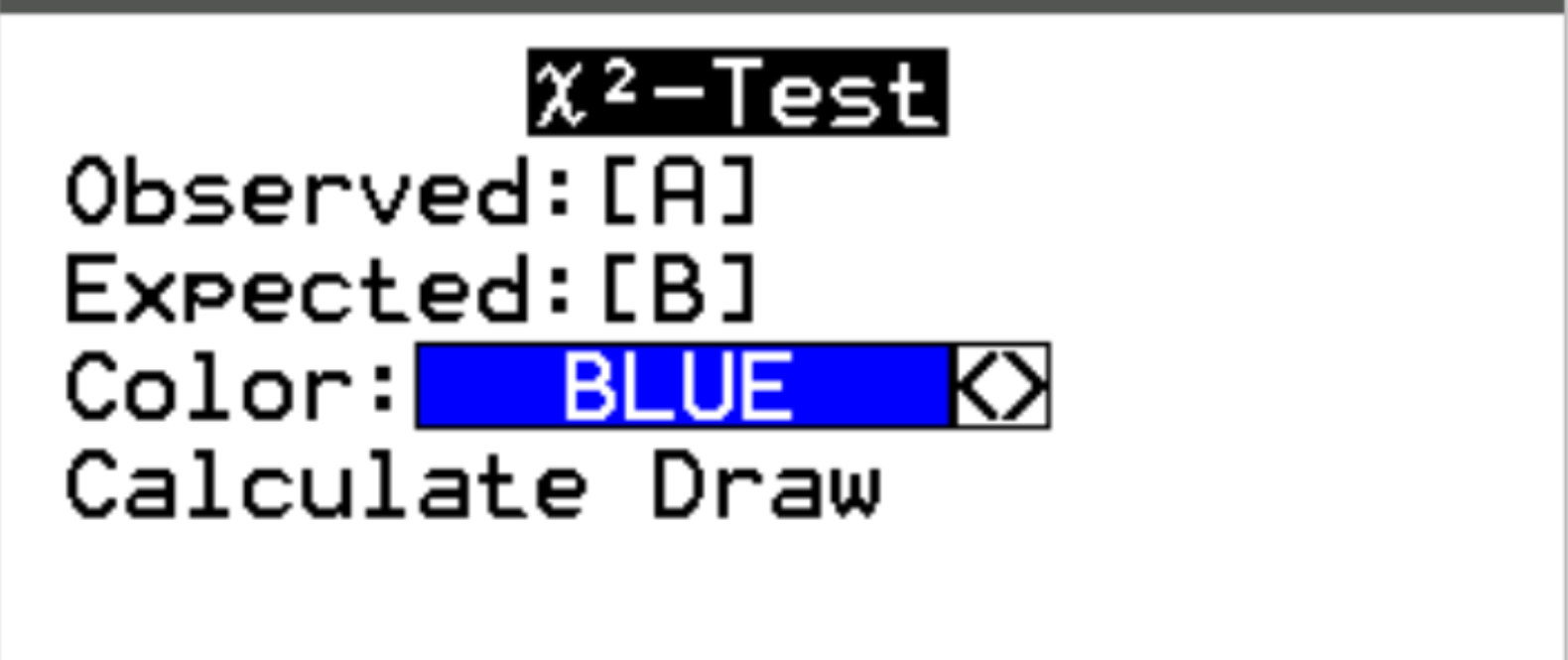
Per Osservato , scegli la matrice in cui hai inserito i dati. Nel nostro caso, abbiamo utilizzato la matrice A. Per Expected può essere qualsiasi matrice vuota (la calcolatrice produrrà automaticamente i valori attesi per noi). Nel nostro caso la lasceremo come matrice B.
Successivamente, evidenzia Calcola e premi Invio .
Verrà visualizzato automaticamente il seguente output:
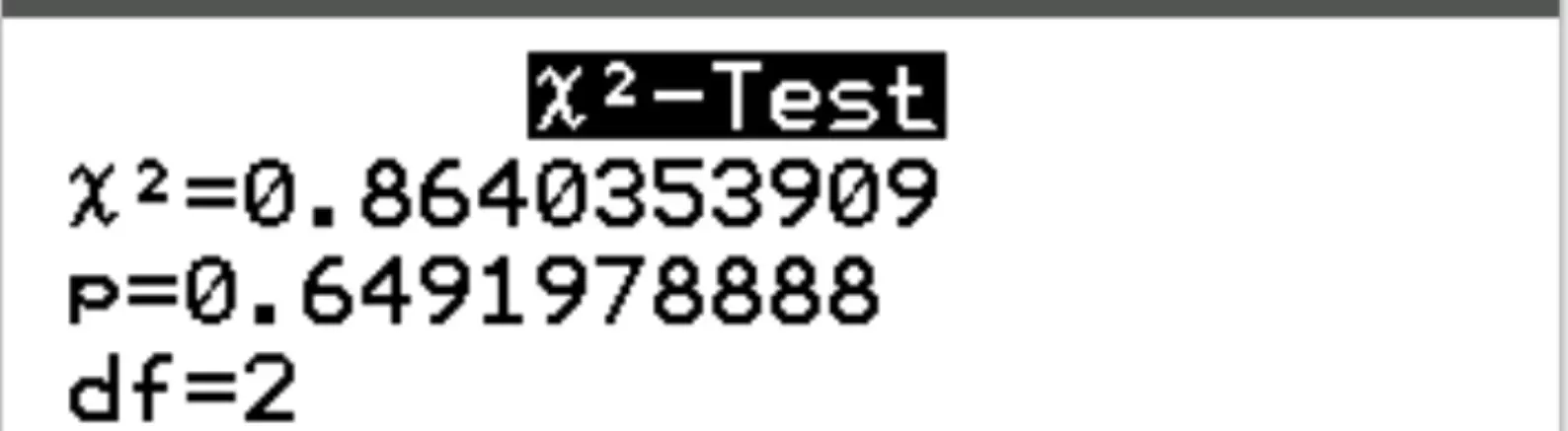
Passaggio 3: interpretare i risultati.
La statistica del test X2 è 0,8640 e il corrispondente valore p è 0,6492 . Poiché questo valore p non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla. Ciò significa che non abbiamo prove sufficienti per affermare che esista un’associazione tra le preferenze di genere e quelle dei partiti politici.