Come calcolare le probabilità binomiali su una calcolatrice ti-84

La distribuzione binomiale è una delle distribuzioni più comunemente utilizzate in tutte le statistiche. Questo tutorial spiega come utilizzare le seguenti funzioni su una calcolatrice TI-84 per trovare le probabilità binomiali:

binompdf(n, p, x) restituisce la probabilità associata al pdf binomiale.

binomcdf(n, p, x) restituisce la probabilità cumulativa associata al cdf binomiale.

Oro:

• n = numero di prove
• p = probabilità di successo in una determinata prova
• x = numero totale di successi

Queste due funzioni sono accessibili su una calcolatrice TI-84 premendo 2nd quindi premendo vars . Questo ti porterà a una schermata DISTR in cui potrai quindi utilizzare binompdf() e binomcdf() :

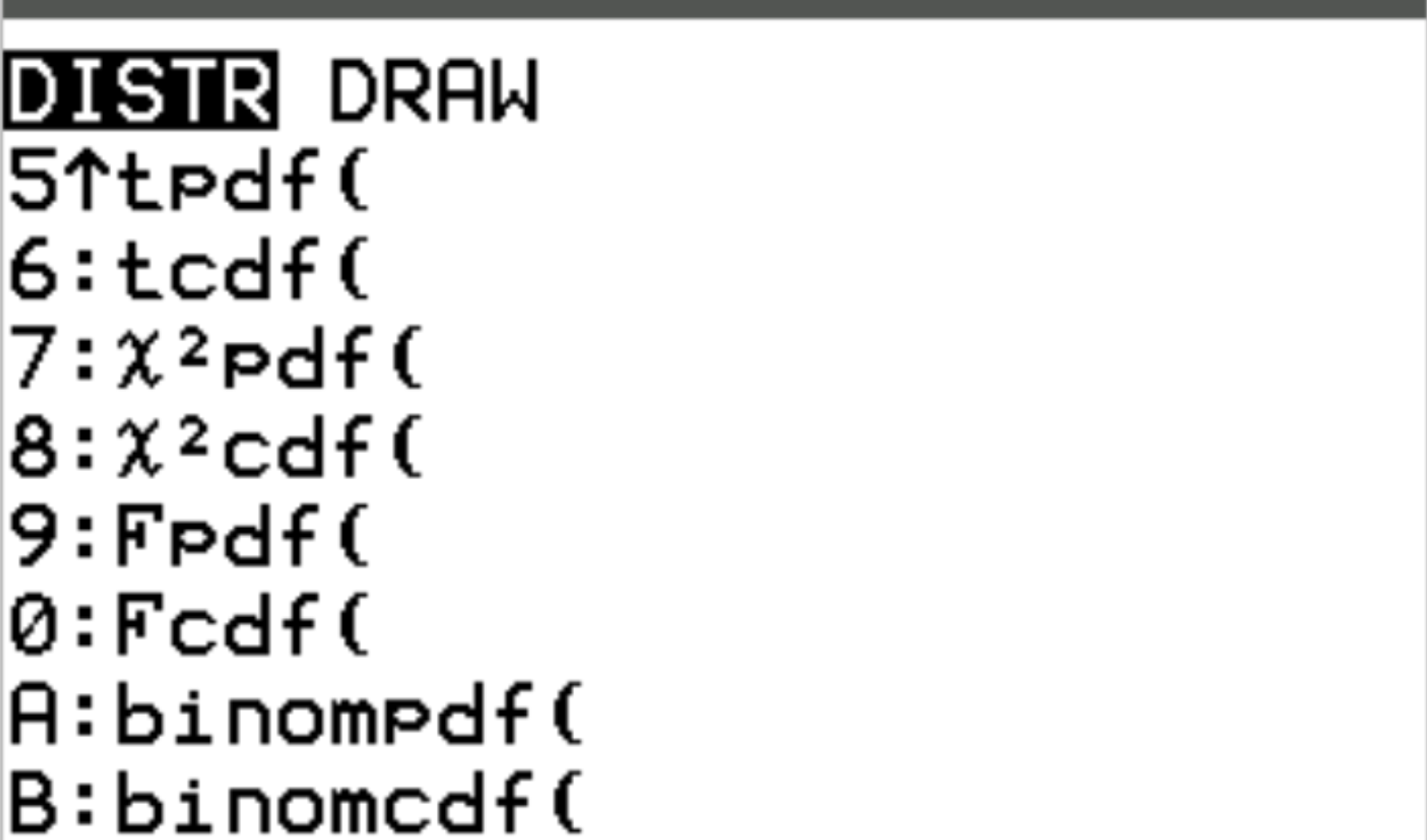
Gli esempi seguenti illustrano come utilizzare queste funzioni per rispondere a domande diverse.

Esempio 1: probabilità binomiale di esattamente x successo

Domanda: Nathan effettua il 60% dei suoi tiri liberi. Se effettua 12 tiri liberi, qual è la probabilità che ne effettui esattamente 10?

Risposta: utilizzare la funzione binomialpdf(n, p, x):

binomialepdf(12, .60, 10) = 0,0639

Esempio 2: probabilità binomiale inferiore a x successo

Domanda: Nathan effettua il 60% dei suoi tiri liberi. Se effettua 12 tiri liberi, qual è la probabilità che ne effettui meno di 10?

Risposta: utilizzare la funzione binomialcdf(n, p, x-1) :

binomialcdf(12, .60, 9) = 0,9166

Esempio 3: probabilità binomiale di al massimo x successo

Domanda: Nathan effettua il 60% dei suoi tiri liberi. Se effettua 12 tiri liberi, qual è la probabilità che ne effettui al massimo 10?

Risposta: utilizzare la funzione binomialcdf(n, p, x) :

binomialcdf(12, .60, 10) = 0,9804

Esempio 4: probabilità binomiale di più di x successi

Domanda: Nathan effettua il 60% dei suoi tiri liberi. Se effettua 12 tiri liberi, qual è la probabilità che ne effettui più di 10?

Risposta: usa la funzione 1 – binomialcdf(n, p, x) :

1 – binomialcdf(12, .60, 10) = 0,0196

Esempio 5: probabilità binomiale di almeno x successo

Domanda: Nathan effettua il 60% dei suoi tiri liberi. Se effettua 12 tiri liberi, qual è la probabilità che ne effettui più di 10?

Risposta: usa la funzione 1 – binomialcdf(n, p, x-1) :

1 – binomialcdf(12, .60, 9) = 0,0834