Socs: un acronimo utile per descrivere le distribuzioni

Nelle statistiche, spesso vogliamo capire come viene distribuito un insieme di dati. In particolare, ci sono quattro cose che è utile sapere su una distribuzione:

1 . Forma

• La distribuzione è simmetrica o sbilanciata da un lato?
• La distribuzione è unimodale (un picco) o bimodale (due picchi)?

2. Valori anomali

• Sono presenti valori anomali nella distribuzione?

3. Centro

• Qual è la media, la mediana e la modalità di distribuzione?

4.Diffusione

• Quali sono l’intervallo, l’intervallo interquartile, la deviazione standard e la varianza della distribuzione?

SOCS è un acronimo utile che possiamo usare per ricordare queste quattro cose. Significa “forma, valori anomali, centro, diffusione”.

Esaminiamo un semplice esempio di come utilizzare SOCS per descrivere una distribuzione.

Esempio: come utilizzare SOCS per descrivere una distribuzione

Supponiamo di avere il seguente set di dati che mostra l’altezza di un campione di 20 piante diverse.

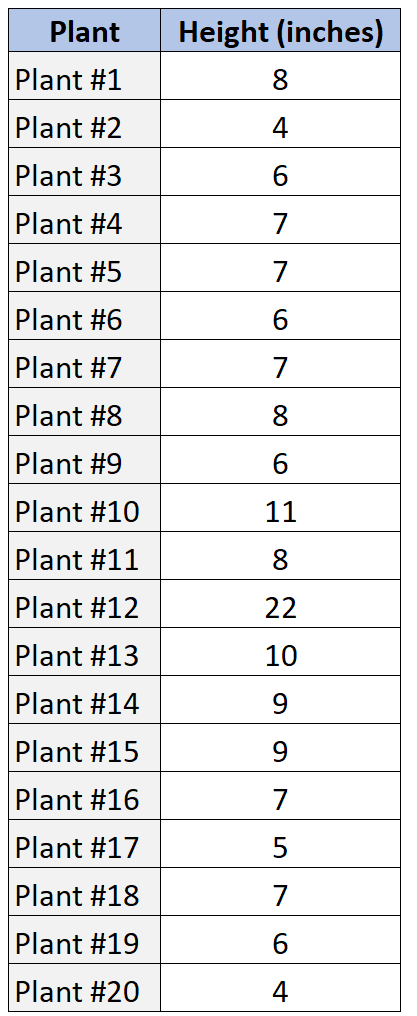
Ecco come possiamo utilizzare SOCS per descrivere questa distribuzione dei valori dei dati.

Forma

Innanzitutto, vogliamo descrivere la forma della distribuzione.

Un modo utile per visualizzare la forma della distribuzione è creare un istogramma che mostri le frequenze di ciascun valore nel set di dati:

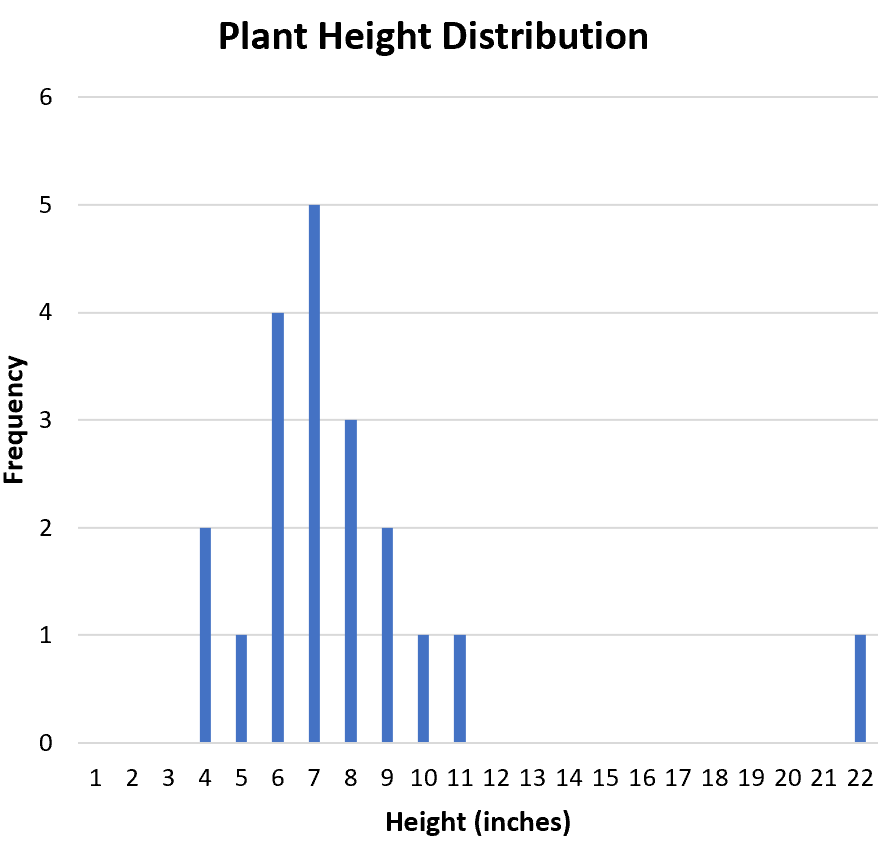
La distribuzione è simmetrica o sbilanciata da un lato?   Dall’istogramma possiamo vedere che la distribuzione è approssimativamente simmetrica. In altre parole, i valori non sono sbilanciati in un senso o nell’altro.

La distribuzione è unimodale (un picco) o bimodale (due picchi)? La distribuzione è unimodale. Ha un picco al valore “7”.

Valori anomali

Successivamente, vogliamo determinare se sono presenti valori anomali nel set di dati. Dall’istogramma possiamo ispezionare visivamente la distribuzione e vedere che 22 è potenzialmente un valore anomalo:

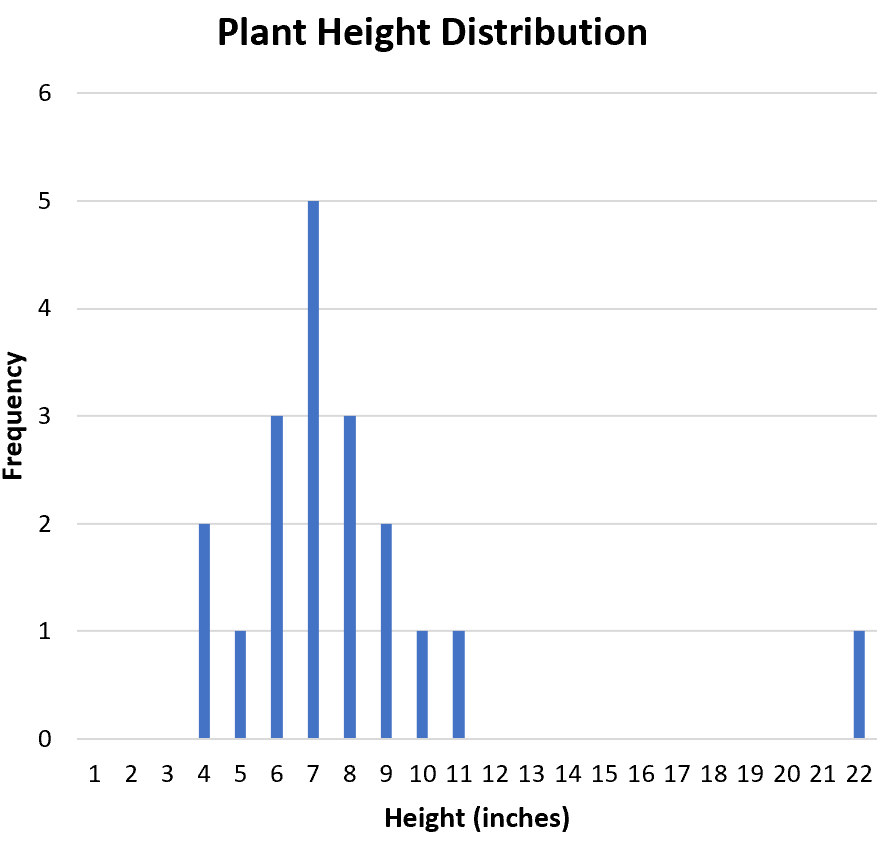
Un modo comune per definire formalmente un valore anomalo è qualsiasi valore che sia 1,5 volte l’intervallo interquartile sopra il terzo quartile o sotto il primo quartile.

Utilizzando il calcolatore dell’intervallo interquartile, possiamo inserire i 20 valori dei dati grezzi e vedere che il terzo quartile è 9 , l’intervallo interquartile è 3 e quindi qualsiasi valore maggiore di 9 + (1,5*3) = 13,5 è un valore anomalo, per definizione.

Poiché 22 è maggiore di 13,5, possiamo dichiarare 22 un valore anomalo.

Centro

Vogliamo poi descrivere dove si trova il centro della distribuzione. Tre misure comuni di tendenza centrale che possiamo utilizzare sono la media, la mediana e la moda.

Media: questo è il valore medio della distribuzione. Lo troviamo sommando tutti i singoli valori e poi dividendo per il numero totale di valori:

Media = (8+4+6+7+7+6+7+8+6+11+8+22+10+9+9+7+5+7+6+4) / 20 = 7,85

Mediana: questo è il valore “medio” della distribuzione. Lo troviamo ordinando tutti i valori dal più piccolo al più grande e identificando poi il valore mediano. Risulta essere 7 .

4, 4, 5, 6, 6, 6, 6, 7, 7, 7 , 7 , 7, 8 , 8, 8, 9, 9, 10, 11, 22

Moda: questo è il valore che appare più frequentemente. Risulta essere 7 .

Diffusione

Successivamente, vogliamo descrivere la distribuzione dei valori nella distribuzione. Quattro misure comuni di dispersione che possiamo utilizzare sono l’intervallo, l’intervallo interquarile, la deviazione standard e la varianza.

Intervallo: questa è la differenza tra il valore più grande e quello più piccolo nel set di dati. Risulta essere 22 – 4 = 18 .

Intervallo interquartile: misura la larghezza del 50% centrale dei valori dei dati. Inserendo i 20 valori dei dati grezzi nel calcolatore dell’intervallo interquartile, possiamo vedere che questo equivale a 3 .

Deviazione standard: questa è una misura della distribuzione media dei valori dei dati. Inserendo i 20 valori dei dati grezzi nel calcolatore della varianza e della deviazione standard, possiamo vedere che la deviazione standard è pari a 3,69 .

Varianza: questa è semplicemente la deviazione standard, al quadrato. Ciò è uguale a 3,69 ² = 13,63 .

Conclusione

Utilizzando SOCS come guida, siamo stati in grado di descrivere la distribuzione dell’altezza delle piante come segue:

• La distribuzione era unimodale e simmetrica, nel senso che aveva un solo picco e non era sbilanciata da una parte o dall’altra.
• La distribuzione aveva un valore anomalo: 22.
• La distribuzione aveva una media di 7,85, una mediana di 7 e una moda di 7.
• La distribuzione aveva un intervallo di 18, un intervallo interquartile di 3, una deviazione standard di 3,69 e una varianza di 13,63.

Tieni presente che possiamo utilizzare SOCS per descrivere qualsiasi distribuzione, il che è un modo utile per comprendere appieno la forma di una distribuzione, se presenta valori anomali, dove si trova approssimativamente il centro e come distribuire i valori Dati. Sono.