Come eseguire un test t per campioni accoppiati in excel

Un test t per campioni accoppiati viene utilizzato per confrontare le medie di due campioni quando ciascuna osservazione in un campione può essere associata a un’osservazione nell’altro campione.

Questo tutorial spiega come eseguire un test t per campioni accoppiati in Excel.

Come eseguire un test t per campioni accoppiati in Excel

Supponiamo di voler sapere se un determinato curriculum ha un impatto significativo sul rendimento degli studenti in un particolare esame. Per testarlo, chiediamo a 20 studenti di una classe di sostenere un pre-test. Quindi facciamo partecipare ciascuno studente al curriculum per due settimane. Quindi, gli studenti ripetono un test di difficoltà simile.

Per confrontare la differenza tra i punteggi medi del primo e del secondo test, utilizziamo un t-test per campioni appaiati perché per ogni studente, il punteggio del primo test può essere associato al punteggio del secondo test.

L’immagine seguente mostra il punteggio pre-test e il punteggio post-test di ogni studente:

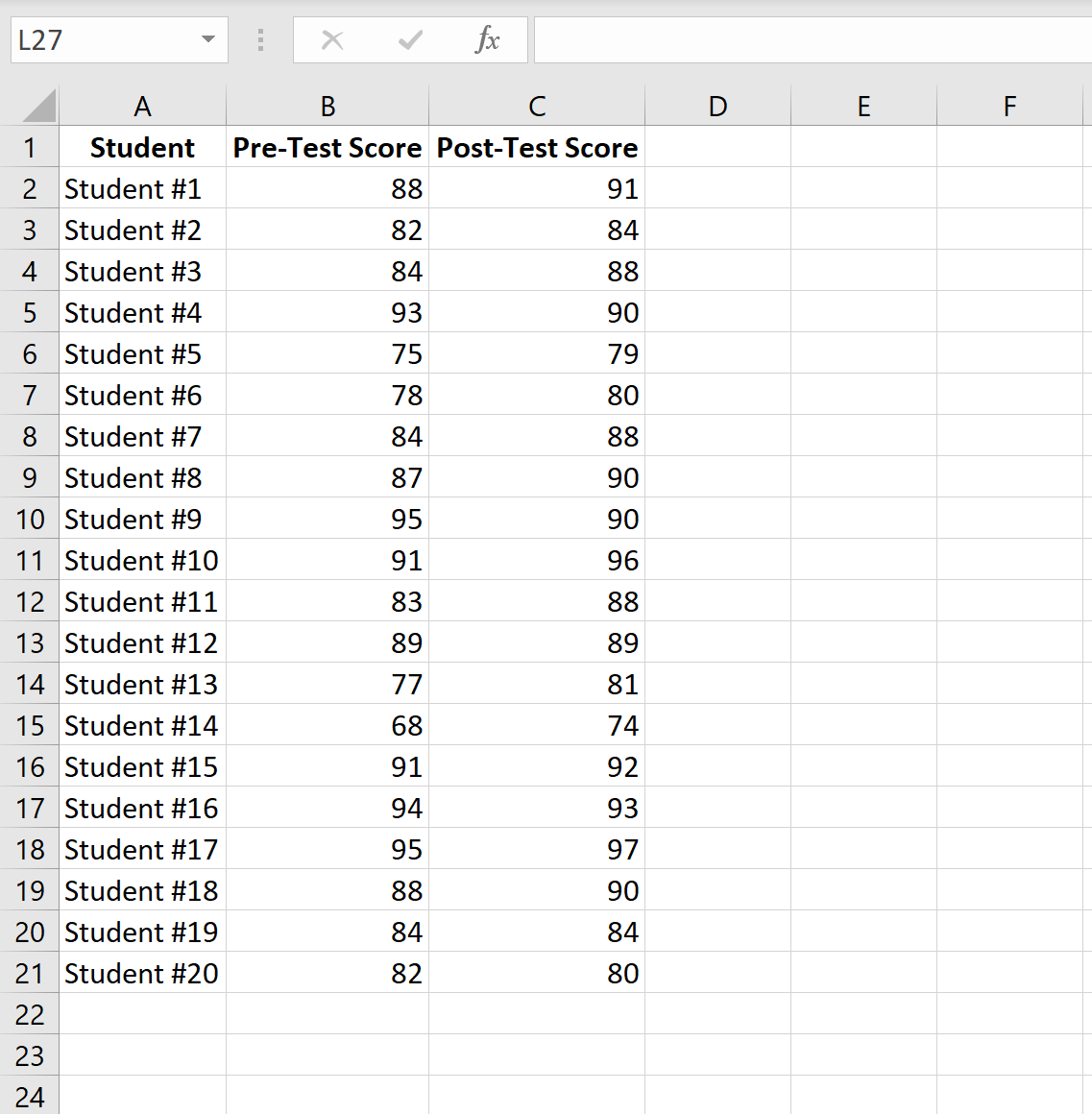
Completare i passaggi seguenti per eseguire un test t per campioni accoppiati per determinare se esiste una differenza significativa nei punteggi medi dei test tra il pre-test e il post-test.

Passaggio 1: aprire il ToolPak per l’analisi dei dati.

Nella scheda Dati della barra multifunzione in alto, fai clic su “Analisi dei dati”.

Se non vedi questa opzione da cliccare, devi prima scaricare Analysis ToolPak , che è completamente gratuito.

Passaggio 2: selezionare il test appropriato da utilizzare.

Selezionare l’opzione che dice T-Test: due campioni accoppiati per medie , quindi fare clic su OK.

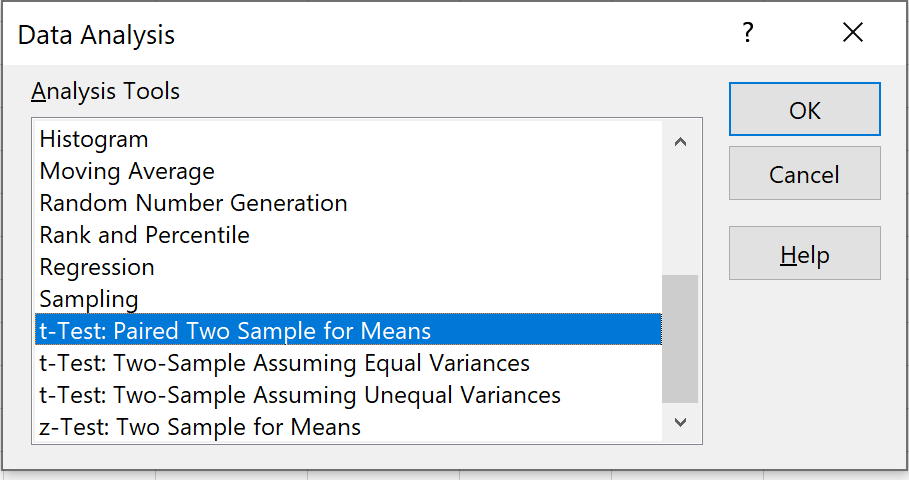
Passaggio 3: inserisci le informazioni necessarie.

Inserisci l’intervallo di valori per la variabile 1 (i punteggi pre-test), la variabile 2 (i punteggi post-test), l’ipotetica differenza media (in questo caso mettiamo “0” perché vogliamo sapere se la vera differenza la media tra i punteggi pre-test e post-test è 0) e l’intervallo di output in cui vorremmo vedere visualizzati i risultati del test. Quindi fare clic su OK.

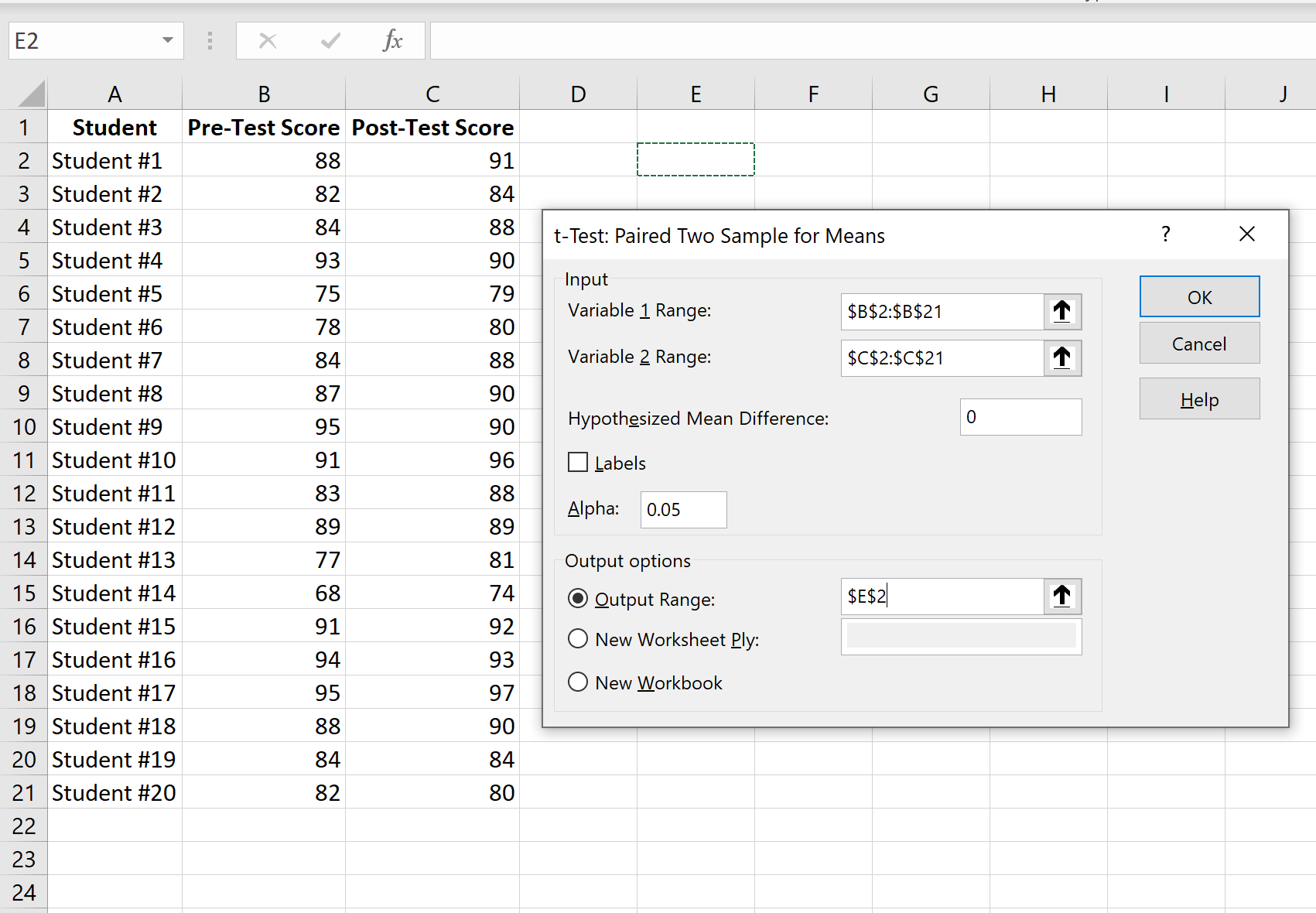
Passaggio 4: interpretare i risultati.

Dopo aver fatto clic su OK nel passaggio precedente, verranno visualizzati i risultati del t-test.

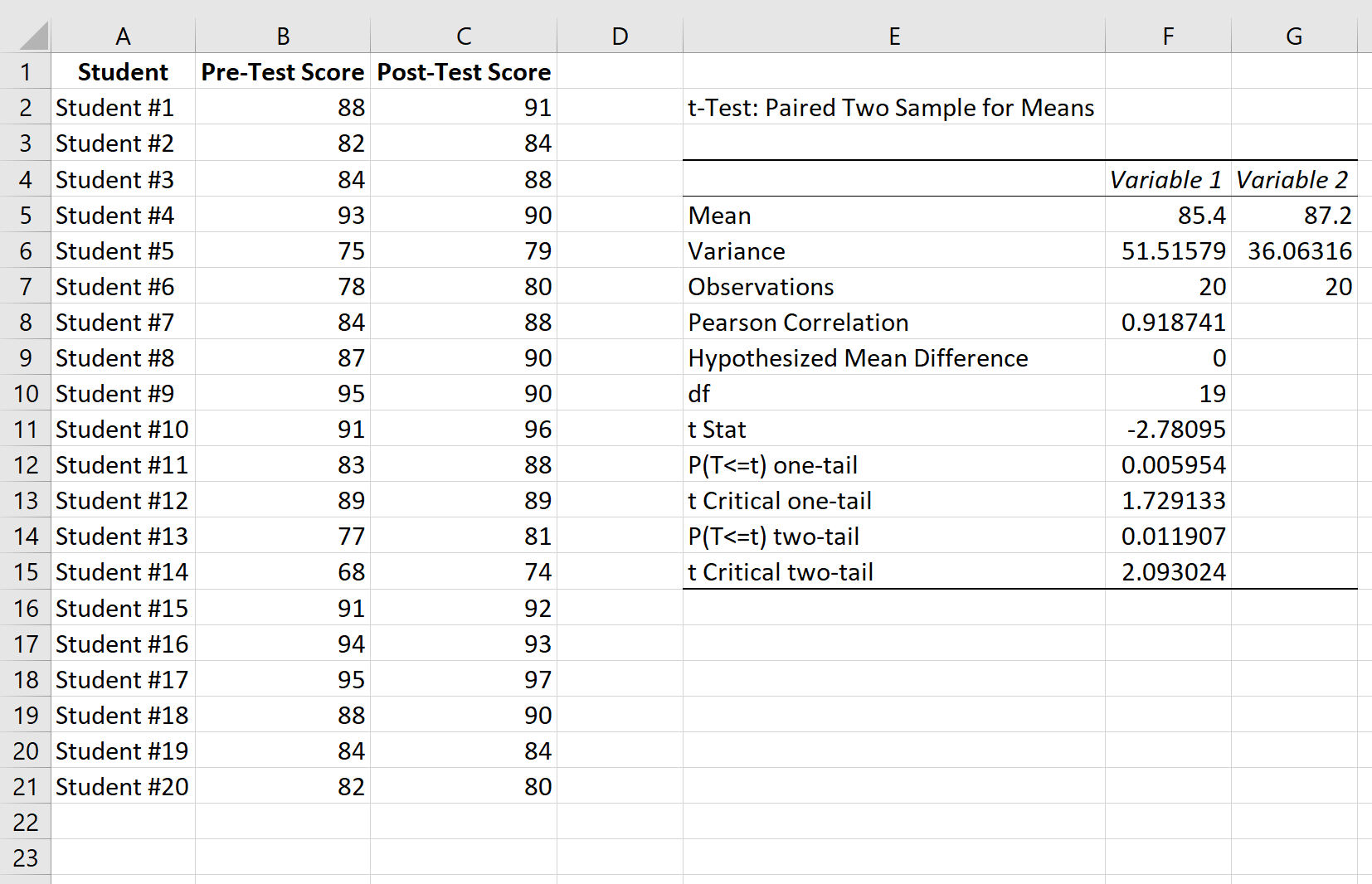
Ecco come interpretare i risultati:

Media: questa è la media di ciascun campione. Il punteggio medio pre-test è 85,4 e il punteggio medio post-test è 87,2 .

Varianza: questa è la varianza per ciascun campione. La varianza dei punteggi pre-test è 51,51 e la varianza dei punteggi post-test è 36,06 .

Osservazioni: questo è il numero di osservazioni in ciascun campione. Entrambi i campioni contengono 20 osservazioni.

Correlazione di Pearson: la correlazione tra i punteggi pre-test e quelli post-test. Risulta essere 0,918 .

Differenza media ipotetica: il numero su cui “ipotizziamo” è la differenza tra le due medie. In questo caso, abbiamo scelto 0 perché vogliamo verificare se esiste o meno una differenza tra i punteggi pre-test e post-test.

df: i gradi di libertà per il test t. Questo viene calcolato come n-1 dove n è il numero di coppie. In questo caso, df = 20 – 1 = 19 .

t Stat: la statistica del test t , che risulta essere -2,78 .

P(T<=t) a due code: il valore p per un test t a due code. In questo caso, p = 0,011907 . Questo è inferiore a alfa = 0,05, quindi rifiutiamo l’ipotesi nulla. Abbiamo prove sufficienti per affermare che esiste una differenza statisticamente significativa tra il punteggio medio pre-test e quello post-test.

t Critico a due code: questo è il valore critico del test, trovato identificando il valore nella tabella di distribuzione t che corrisponde a un test a due code con alfa = 0,05 e df = 19. Questo risulta essere 2, 093024 . Poiché il valore assoluto della nostra statistica t -test è maggiore di questo valore, rifiutiamo l’ipotesi nulla. Abbiamo prove sufficienti per affermare che esiste una differenza statisticamente significativa tra il punteggio medio pre-test e quello post-test.

Si noti che l’approccio del valore p e del valore critico porteranno entrambi alla stessa conclusione.

Risorse addizionali

I seguenti tutorial spiegano come eseguire altri test t in Excel:

Come eseguire un test t per un campione in Excel
Come eseguire un test t a due campioni in Excel