Come eseguire un test di adattamento chi quadrato in stata

Un test di bontà di adattamento chi quadrato viene utilizzato per determinare se una variabile categoriale segue o meno una distribuzione ipotetica.

Questo tutorial spiega come eseguire un test di bontà di adattamento del chi quadrato in Stata.

Esempio: test di bontà di adattamento del chi quadrato in Stata

Per illustrare come eseguire questo test, utilizzeremo un set di dati chiamato nlsw88 , che contiene informazioni sulle statistiche del lavoro femminile negli Stati Uniti nel 1988.

Seguire i passaggi seguenti per eseguire un test di bontà di adattamento chi quadrato per determinare se la vera distribuzione della razza in questo set di dati è: 70% bianchi, 20% neri, 10% altro.

Passaggio 1: caricare e visualizzare i dati grezzi.

Per prima cosa caricheremo i dati digitando il seguente comando:

sistema nlsw88

Possiamo visualizzare i dati grezzi digitando il seguente comando:

fratello

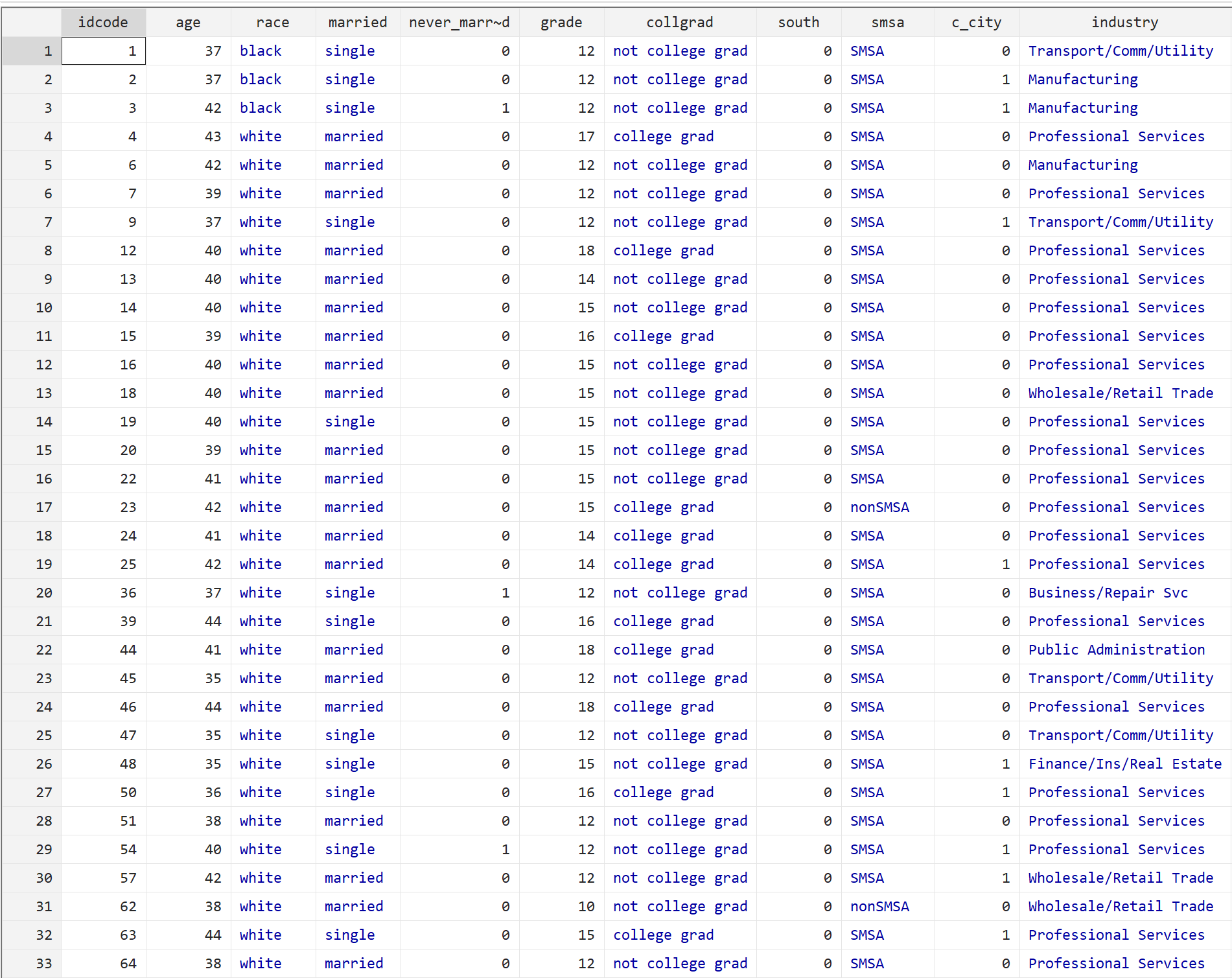
Ogni riga visualizza informazioni su un individuo, tra cui età, razza, stato civile, livello di istruzione e vari altri fattori.

Passaggio 2: caricare il pacchetto di aggiustamenti.

Per eseguire un test di idoneità, dovremo installare il pacchetto csgof . Possiamo farlo digitando il seguente comando:

trova csgof

Apparirà una nuova finestra. Fare clic sul collegamento che dice csgof da https://stats.idre.ucla.edu/stat/stata/ado/analysis .

Apparirà un’altra finestra. Fare clic sul collegamento che dice fare clic qui per installare .

L’installazione del pacchetto dovrebbe richiedere solo pochi secondi.

Passaggio 3: eseguire il test di adattamento.

Una volta installato il pacchetto, possiamo eseguire il test di adattamento sui dati per determinare se la vera ripartizione della razza è: 70% bianco, 20% nero, 10% altro.

Utilizzeremo la seguente sintassi per eseguire il test:

csgof variabile_di_interesse, expperc(elenco_delle_percentuali_previste)

Ecco la sintassi esatta che utilizzeremo nel nostro caso:

esegui csgof, expperc(70, 20, 10)

Ecco come interpretare il risultato:

Riquadro riepilogativo: questo riquadro mostra la percentuale prevista, la frequenza prevista e la frequenza osservata per ciascuna gara. Per esempio:

• La percentuale prevista di individui bianchi era del 70%. Questa è la percentuale che abbiamo specificato.
• La frequenza prevista degli individui bianchi era 1.572,2. Questo viene calcolato utilizzando il fatto che nel set di dati erano presenti 2.246 individui, quindi il 70% di quel numero è 1.572,2.
• La frequenza osservata di individui bianchi era 1.637. Questo è il numero effettivo di individui bianchi nel set di dati.

Chisq(2): questa è la statistica del test Chi-quadrato per il test della bontà di adattamento. Risulta essere 218.13.

p: questo è il valore p associato alla statistica del test Chi-quadrato. Risulta essere 0. Poiché è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla secondo cui la vera distribuzione razziale è 70% bianchi, 20% neri e 10% Altri. Abbiamo prove sufficienti per concludere che la vera distribuzione razziale è diversa da questa ipotetica distribuzione.