Come calcolare il coefficiente di correlazione di matthews in r

Il coefficiente di correlazione di Matthews (MCC) è una metrica che possiamo utilizzare per valutare le prestazioni di unmodello di classificazione .

Viene calcolato come segue:

Centro clienti = (TP*TN – FP*FN) / √ (TP+FP)(TP+FN)(TN+FP)(TN+FN)

Oro:

• TP : numero di veri positivi
• TN : numero di veri negativi
• FP : Numero di falsi positivi
• FN : Numero di falsi negativi

Questa metrica è particolarmente utile quando le due classi sono sbilanciate, ovvero una classe appare molto più dell’altra.

Il valore di MCC è compreso tra -1 e 1 dove:

• -1 indica un disaccordo totale tra le classi previste e le classi effettive
• 0 significa ipotesi completamente casuali
• 1 indica un completo accordo tra le classi previste e le classi effettive

Supponiamo, ad esempio, che un analista sportivo utilizzi un modello di regressione logistica per prevedere se 400 diversi giocatori di basket universitari verranno arruolati o meno nella NBA.

La seguente matrice di confusione riassume le previsioni fatte dal modello:

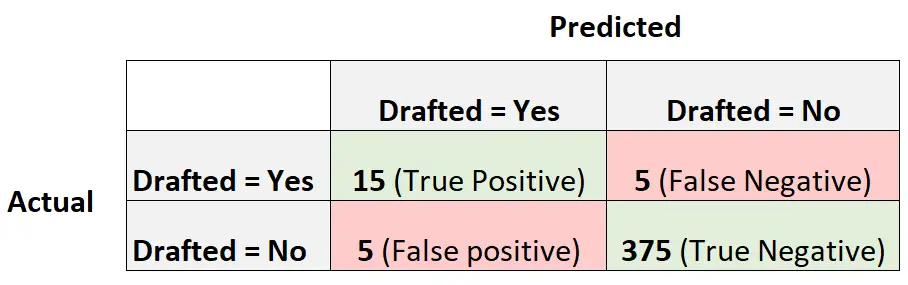
Per calcolare l’MCC del modello, possiamo utilizzare la seguente formula:

• Centro clienti = (TP*TN – FP*FN) / √ (TP+FP)(TP+FN)(TN+FP)(TN+FN)
• Centro clienti = (15*375-5*5) / √ (15+5)(15+5)(375+5)(375+5)
• Centro clienti = 0,7368

Il coefficiente di correlazione di Matthews risulta essere 0,7368 .

Questo valore è piuttosto vicino a uno, indicando che il modello sta facendo un buon lavoro nel prevedere se i giocatori verranno scelti o meno.

L’esempio seguente mostra come calcolare il Centro clienti per questo scenario specifico utilizzando la funzione mcc() del pacchetto mltools in R.

Esempio: calcolo del coefficiente di correlazione di Matthews in R

Il codice seguente mostra come definire un vettore di classi previste e un vettore di classi effettive, quindi calcolare il coefficiente di correlazione di Matthews utilizzando la funzione mcc() del pacchetto mltools :

 library (mltools)

#define vector of actual classes
actual <- rep (c(1, 0), times =c(20, 380))

#define vector of predicted classes
preds <- rep (c(1, 0, 1, 0), times =c(15, 5, 5, 375))

#calculate Matthews correlation coefficient
mcc(preds, actual)

[1] 0.7368421

Il coefficiente di correlazione di Matthews è 0,7368 .

Questo corrisponde al valore che abbiamo calcolato manualmente in precedenza.

Se vuoi calcolare il coefficiente di correlazione Matthews per una matrice di confusione, puoi utilizzare l’argomento confusionM come segue:

 library (mltools)

#create confusion matrix
conf_matrix <- matrix(c(15, 5, 5, 375), nrow= 2 )

#view confusion matrix
conf_matrix

     [,1] [,2]
[1,] 15 5
[2,] 5,375

#calculate Matthews correlation coefficient for confusion matrix
mcc(confusionM = conf_matrix)

[1] 0.7368421

Ancora una volta, il coefficiente di correlazione di Matthews è 0,7368.

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in R:

Come eseguire la regressione logistica in R
Come tracciare una curva ROC utilizzando ggplot2
Come calcolare il punteggio F1 in R