Coefficiente di correlazione di pearson

Il coefficiente di correlazione di Pearson (noto anche come “coefficiente di correlazione prodotto-momento”) è una misura dell’associazione lineare tra due variabili X e Y. Ha un valore compreso tra -1 e 1 dove:

• -1 indica una correlazione lineare perfettamente negativa tra due variabili
• 0 indica alcuna correlazione lineare tra due variabili
• 1 indica una correlazione lineare perfettamente positiva tra due variabili

La formula per trovare il coefficiente di correlazione di Pearson

La formula per trovare il coefficiente di correlazione di Pearson, indicato con r , per un campione di dati è ( tramite Wikipedia ):

Probabilmente non dovrai mai calcolare questa formula a mano poiché puoi utilizzare un software per farlo per te, ma è utile capire cosa fa esattamente questa formula seguendo un esempio.

Supponiamo di avere il seguente set di dati:

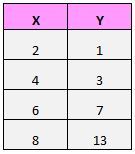
Se tracciassimo queste coppie (X, Y) su un grafico a dispersione, assomiglierebbe a questo:

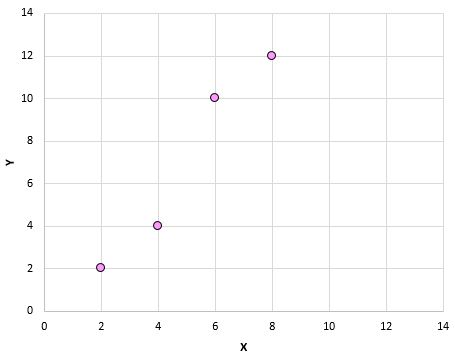
Semplicemente osservando questo grafico a dispersione, possiamo vedere che esiste un’associazione positiva tra le variabili X e Y: all’aumentare di X, anche Y tende ad aumentare. Ma per quantificare esattamente quanto positivamente sono associate queste due variabili, dobbiamo trovare il coefficiente di correlazione di Pearson.

Concentriamoci solo sul numeratore della formula:

Per ogni coppia (X, Y) nel nostro set di dati, dobbiamo trovare la differenza tra il valore x e il valore medio x, la differenza tra il valore y e il valore medio y, quindi moltiplicare questi due numeri insieme.

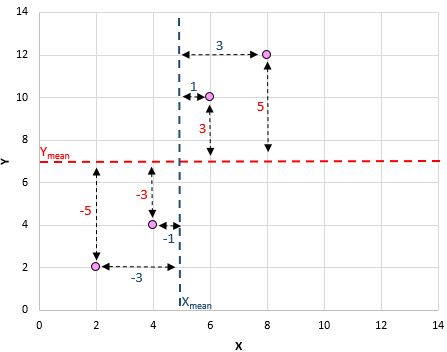
Ad esempio, la nostra prima coppia (X, Y) è (2, 2). Il valore medio di x in questo set di dati è 5 e il valore medio di y in questo set di dati è 7. Quindi la differenza tra il valore x di questa coppia e il valore medio di x è 2 – 5 = -3. La differenza tra il valore y di questa coppia e il valore y medio è 2 – 7 = -5. Quindi moltiplicando questi due numeri otteniamo -3 * -5 = 15.

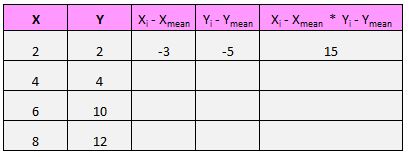
Ecco una panoramica visiva di ciò che abbiamo appena fatto:

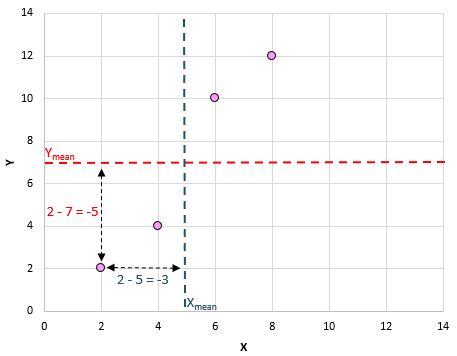
Quindi fai questo per ogni coppia:

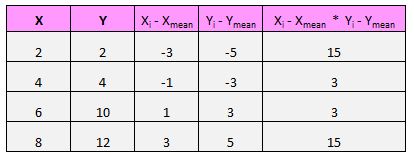
Il passaggio finale per ottenere il numeratore della formula è semplicemente sommare tutti questi valori insieme:

15+3+3+15 = 36

Quindi il denominatore della formula ci dice di trovare la somma di tutte le differenze al quadrato di xey, quindi moltiplicare questi due numeri insieme e infine calcolare la radice quadrata:

Quindi prima troveremo la somma dei quadrati delle differenze per x e y:

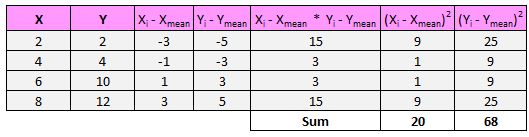
Successivamente, moltiplicheremo questi due numeri insieme: 20 * 68 = 1.360.

Infine, prenderemo la radice quadrata: √ 1.360 = 36,88

Quindi abbiamo scoperto che il numeratore della formula è 36 e il denominatore è 36,88. Ciò significa che il nostro coefficiente di correlazione di Pearson è r = 36 / 36,88 = 0,976

Questo numero è vicino a 1, indicando che esiste una forte relazione lineare positiva tra le nostre variabili X e Y. Ciò conferma la relazione che abbiamo osservato nel grafico a dispersione.

Visualizza correlazioni

Ricorda che un coefficiente di correlazione di Pearson ci dice il tipo di relazione lineare (positiva, negativa, nessuna) tra due variabili e la forza di questa relazione (debole, moderata, forte).

Quando creiamo un grafico a dispersione di due variabili, possiamo vedere la relazione reale tra due variabili. Ecco i molti tipi di relazioni lineari che potremmo osservare:

Relazione forte e positiva: all’aumentare della variabile sull’asse x, aumenta anche la variabile sull’asse y. I punti sono strettamente raggruppati, indicando una forte relazione.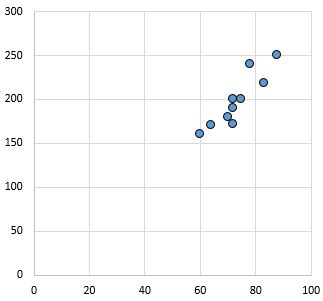

Coefficiente di correlazione di Pearson: 0,94

Relazione debole e positiva: all’aumentare della variabile sull’asse x, aumenta anche la variabile sull’asse y. I punti sono piuttosto sparsi, indicando una relazione debole.

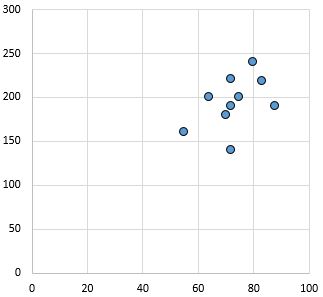
Coefficiente di correlazione di Pearson: 0,44

Nessuna relazione: non esiste una relazione chiara (positiva o negativa) tra le variabili.

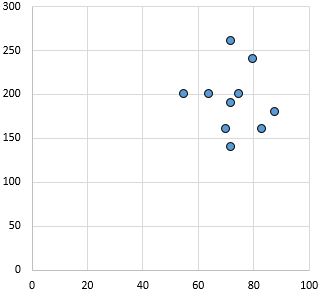
Coefficiente di correlazione di Pearson: 0,03

Relazione forte e negativa: all’aumentare della variabile sull’asse x, la variabile sull’asse y diminuisce. I punti sono strettamente raggruppati, indicando una forte relazione.

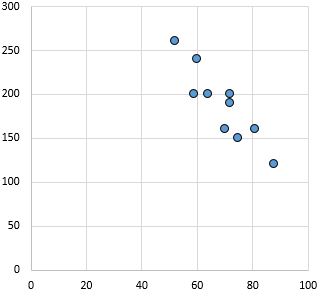
Coefficiente di correlazione di Pearson: -0,87

Relazione debole e negativa: all’aumentare della variabile sull’asse x, la variabile sull’asse y diminuisce. I punti sono piuttosto sparsi, indicando una relazione debole.

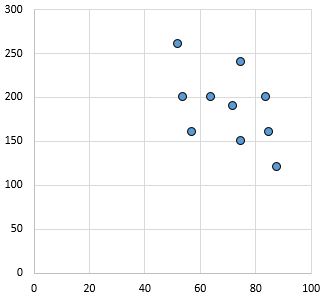
Coefficiente di correlazione di Pearson: – 0,46

Testare la significatività di un coefficiente di correlazione di Pearson

Quando troviamo il coefficiente di correlazione di Pearson per un insieme di dati, spesso lavoriamo con un campione di dati proveniente da una popolazione più ampia. Ciò significa che è possibile trovare una correlazione diversa da zero per due variabili anche se in realtà non sono correlate nella popolazione complessiva.

Ad esempio, supponiamo di creare un grafico a dispersione per le variabili X e Y per ciascun punto dati dell’intera popolazione e che assomigli a questo:

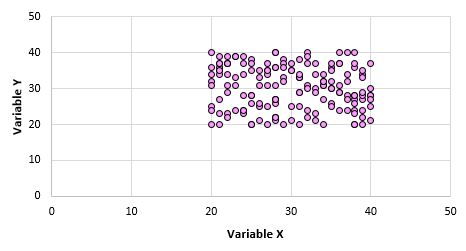
È ovvio che queste due variabili non sono correlate. Tuttavia, è possibile che quando prendiamo un campione di 10 punti dalla popolazione, scegliamo i seguenti punti:

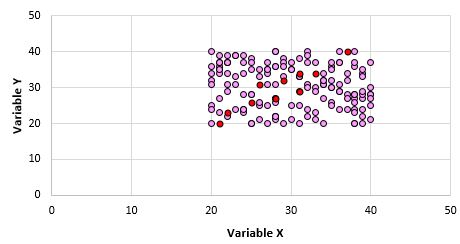
Possiamo vedere che il coefficiente di correlazione di Pearson per questo campione di punti è 0,93, indicando una forte correlazione positiva anche se la correlazione della popolazione è zero.

Per verificare se una correlazione tra due variabili è statisticamente significativa o meno, possiamo trovare la seguente statistica test:

Statistica del test T = r * √ (n-2) / (1-r ² )

dove n è il numero di coppie nel nostro campione, r è il coefficiente di correlazione di Pearson e la statistica del test T segue una distribuzione con n-2 gradi di libertà.

Rivediamo un esempio di come testare la significatività di un coefficiente di correlazione di Pearson.

Esempio

Il seguente set di dati mostra l’altezza e il peso di 12 individui:

Il grafico a dispersione seguente mostra il valore di queste due variabili:

Il coefficiente di correlazione di Pearson per queste due variabili è r = 0,836.

La statistica del test T = 0,836 * √ (12 -2) / (1-0,836 ² ) = 4,804.

Secondo il nostro calcolatore della distribuzione t , un punteggio di 4,804 con 10 gradi di libertà ha un valore p di 0,0007. Poiché 0,0007 < 0,05, possiamo concludere che la correlazione tra peso e altezza in questo esempio è statisticamente significativa con alfa = 0,05.

Precauzioni

Sebbene un coefficiente di correlazione di Pearson possa essere utile per dirci se due variabili hanno o meno un’associazione lineare, dobbiamo tenere a mente tre cose quando interpretiamo un coefficiente di correlazione di Pearson:

1. La correlazione non implica causalità. Non è perché due variabili sono correlate che una faccia necessariamente apparire l’altra più o meno spesso. Un classico esempio di ciò è la correlazione positiva tra le vendite di gelati e gli attacchi di squali. Quando le vendite di gelati aumentano in determinati periodi dell’anno, tendono ad aumentare anche gli attacchi di squali.

Questo significa che mangiare il gelato provoca attacchi di squali? Ovviamente no! Ciò significa semplicemente che in estate il consumo di ghiaccio e gli attacchi di squali tendono ad aumentare, perché il ghiaccio è più popolare in estate e più persone vanno nell’oceano durante l’estate.

2. Le correlazioni sono sensibili ai valori anomali. Un valore anomalo estremo può modificare in modo significativo un coefficiente di correlazione di Pearson. Considera l’esempio seguente:

Le variabili X e Y hanno un coefficiente di correlazione di Pearson pari a 0,00 . Ma immaginiamo di avere un valore anomalo nel set di dati:

Tuttavia, il coefficiente di correlazione di Pearson per queste due variabili è 0,878 . Questo valore anomalo cambia tutto. Questo è il motivo per cui, quando si calcola la correlazione tra due variabili, è una buona idea visualizzare le variabili utilizzando un grafico a dispersione per verificare la presenza di valori anomali.

3. Un coefficiente di correlazione di Pearson non cattura le relazioni non lineari tra due variabili. Immaginiamo di avere due variabili con la seguente relazione:

Il coefficiente di correlazione di Pearson per queste due variabili è 0,00 perché non hanno una relazione lineare. Tuttavia, queste due variabili hanno una relazione non lineare: i valori y sono semplicemente i valori x al quadrato.

Quando utilizzi il coefficiente di correlazione di Pearson, tieni presente che stai semplicemente verificando se due variabili sono correlate linearmente . Anche se un coefficiente di correlazione di Pearson ci dice che due variabili non sono correlate, potrebbero comunque avere qualche tipo di relazione non lineare. Questo è un altro motivo per cui è utile creare un grafico a dispersione quando si analizza la relazione tra due variabili: può aiutarti a rilevare una relazione non lineare.