Coefficiente di correlazione di pearson

Di Benjamin anderson Agosto 5, 2023 Statistiche 0 commenti

Questo articolo spiega cos’è il coefficiente di correlazione di Pearson (o coefficiente di correlazione lineare) e a cosa serve. Scoprirai come calcolare il coefficiente di correlazione di Pearson insieme a un esercizio passo passo. Inoltre, puoi trovare il valore del coefficiente di correlazione di Pearson di qualsiasi set di dati con il calcolatore online alla fine.

Qual è il coefficiente di correlazione di Pearson?

Il coefficiente di correlazione di Pearson , chiamato anche coefficiente di correlazione lineare o semplicemente coefficiente di correlazione , è una misura statistica che indica la relazione tra due variabili.

Per calcolare il coefficiente di correlazione di Pearson tra due variabili, è necessario dividere la covarianza di tali variabili per la radice quadrata del prodotto delle loro varianze.

Pertanto, il coefficiente di correlazione di Pearson tenta di quantificare la dipendenza lineare tra due variabili casuali quantitative. A priori, valutare numericamente la correlazione tra variabili è complicato perché è difficile determinare quale coppia di variabili sia più correlata tra se, come in pues, lo scopo del coefficiente di correlazione di Pearson è quello di valutare la relazione tra variabili per poter confrontare tra loro.

Il valore dell’indice di correlazione di Pearson è compreso tra -1 e +1 compresi. Vedremo di seguito come viene interpretato il valore del coefficiente di correlazione di Pearson.

Formula del coefficiente di correlazione di Pearson

Il coefficiente di correlazione di Pearson di due variabili statistiche è pari al quoziente tra la covarianza delle variabili e la radice quadrata del prodotto della varianza di ciascuna variabile.

Pertanto, la formula per calcolare il coefficiente di correlazione di Pearson è la seguente:

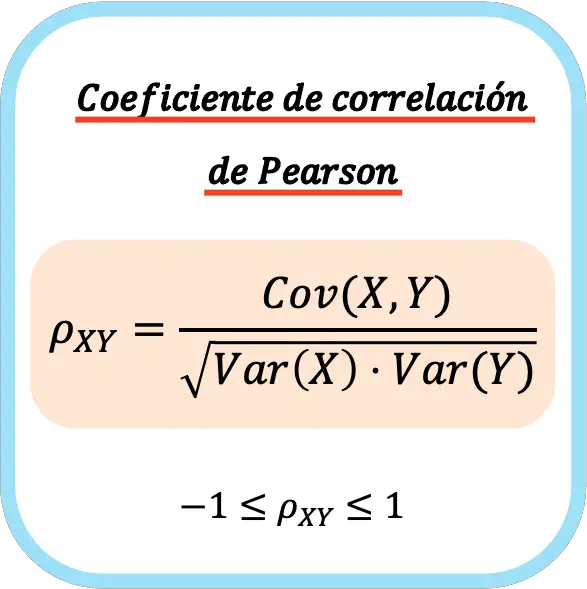
Coefficiente di correlazione di Pearson, coefficiente di correlazione lineare

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare il coefficiente di correlazione di Pearson per qualsiasi set di dati.

Quando il coefficiente di correlazione di Pearson viene calcolato su una popolazione, viene generalmente espresso con la lettera greca ρ. Ma quando il coefficiente viene calcolato rispetto a un campione, di solito viene utilizzata la lettera r come simbolo.

Tieni presente che per determinare il coefficiente di correlazione di Pearson è essenziale sapere come calcolare la covarianza tra due variabili e la varianza di una variabile. Inoltre, è necessario capire cosa significano queste misure statistiche. Pertanto, prima di proseguire nella spiegazione, si consiglia di leggere i due articoli seguenti:

➤ Vedi: come calcolare la covarianza
➤ Vedi: come calcolare il gap

Esempio di calcolo del coefficiente di correlazione di Pearson

Considerando la definizione del coefficiente di correlazione di Pearson e la sua formula, di seguito è riportato un esempio passo passo in modo da poter vedere come viene calcolato.

Calcolare il coefficiente di correlazione di Pearson tra le seguenti due variabili continue:

Prima di calcolare il coefficiente di correlazione di Pearson, rappresenteremo il set di dati in un grafico a dispersione per analizzare la relazione tra le due variabili:

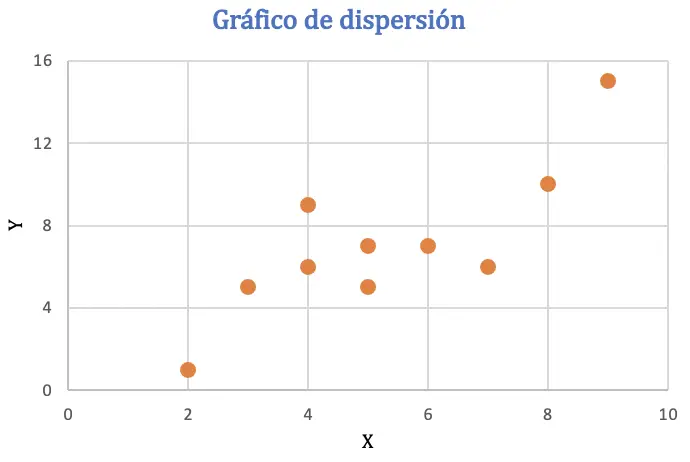
Dal grafico a dispersione si può dedurre che i dati possono avere un andamento positivo, ovvero quando una variabile aumenta di valore anche l’altra variabile aumenta. Per verificare la correlazione, troveremo il coefficiente di Pearson.

La prima cosa da fare è trovare separatamente la media aritmetica di ciascuna variabile, che equivale alla somma totale dei dati divisa per il numero di osservazioni.

$\overline{x}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}=\cfrac{53}{10}=5,3$

$\overline{y}=\cfrac{\displaystyle \sum_{i=1}^n y_i}{n}=\cfrac{71}{10}=7,1$

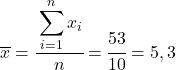
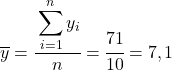
Ora che conosciamo la media di ciascuna variabile, dobbiamo aggiungere le seguenti colonne alla tabella dati:

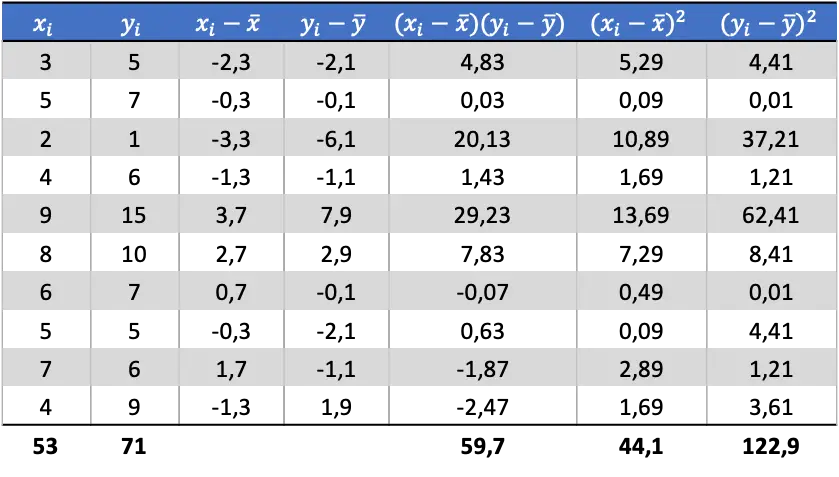
Tabella dati per il calcolo del coefficiente di Pearson

Dai dati calcolati nella tabella, determiniamo i valori della covarianza e delle varianze (se non ricordi come è stato fatto, ci sono due link sopra dove è spiegato in dettaglio):

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}=\cfrac{59,7}{10}=5,97$

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}=\cfrac{44,1}{10}=4,41$

$Var(Y)=\cfrac{\displaystyle\sum_{i=1}^n\left(y_i-\overline{y}\right)^2}{n}=\cfrac{122,9}{10}=12,29$

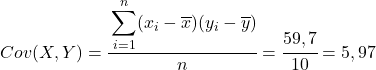
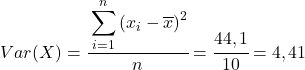
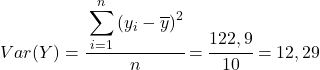
Infine, basta applicare la formula del coefficiente di correlazione di Pearson per ottenerne il valore:

$\rho_{XY}=\cfrac{Cov(X,Y)}{\sqrt{Var(X)\cdot Var(Y)}}=\cfrac{5,97}{\sqrt{4,41\cdot 12,29}}=0,81$

Il coefficiente di correlazione di Pearson ha un valore molto vicino a 1, il che significa che queste due variabili hanno una correlazione positiva abbastanza forte.

Come hai visto, per determinare il coefficiente di correlazione di Pearson è molto utile utilizzare programmi come Excel per eseguire più rapidamente i calcoli delle colonne.

Calcolatore del coefficiente di correlazione di Pearson

Inserisci una serie di dati statistici nella seguente calcolatrice per calcolare il coefficiente di correlazione di Pearson tra due variabili. È necessario separare le coppie di dati, in modo che nella prima casella ci siano solo i valori di una variabile e nella seconda casella ci siano solo i valori della seconda variabile.

I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Interpretazione del coefficiente di correlazione di Pearson

In questa sezione vedremo come interpretare il coefficiente di correlazione di Pearson, perché non basta conoscerne il valore, ma bisogna saperne analizzare il significato.

Pertanto l’ interpretazione del coefficiente di correlazione di Pearson dipende dal suo valore:

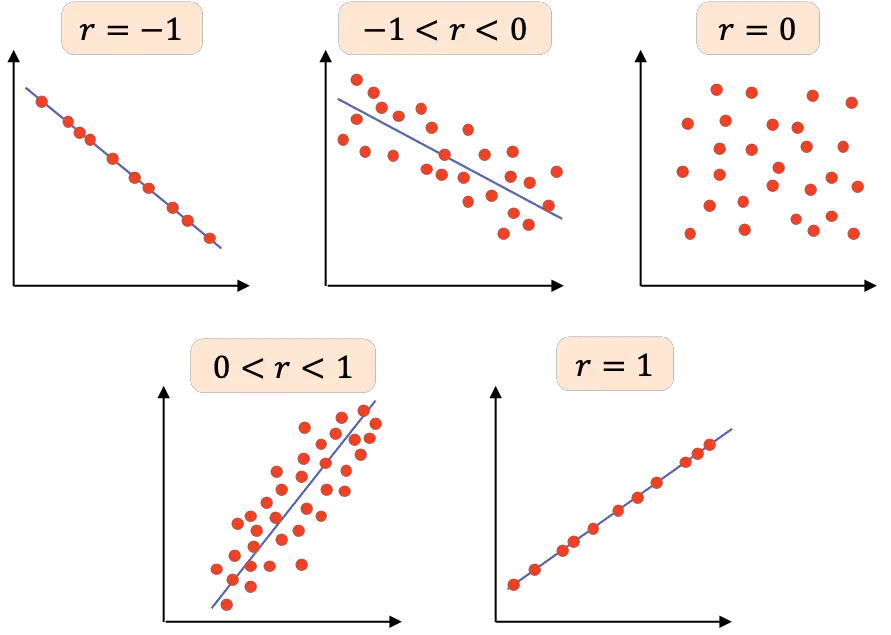
r=-1 : le due variabili hanno una perfetta correlazione negativa, quindi possiamo tracciare una linea con pendenza negativa in cui tutti i punti si collegano.
-1<r<0 : la correlazione tra le due variabili è negativa, quindi quando una variabile aumenta l’altra diminuisce. Più il valore è vicino a -1, più le variabili sono correlate negativamente.
r=0 : la correlazione tra le due variabili è molto debole, infatti la relazione lineare tra loro è zero. Ciò non significa che le variabili siano indipendenti, poiché potrebbero avere una relazione non lineare.
0<r<1 : la correlazione tra le due variabili è positiva, più il valore è vicino a +1, più forte è la relazione tra le variabili. In questo caso una variabile tende ad aumentare di valore quando aumenta anche l’altra.
r=1 : le due variabili hanno una perfetta correlazione positiva, cioè hanno una relazione lineare positiva.

In sintesi, la tabella seguente viene presentata con le diverse interpretazioni del coefficiente di correlazione di Pearson:

Valore	Interpretazione
r=-1	Correlazione negativa perfetta.
-1<r<0	Correlazione negativa: più la correlazione è vicina a -1, più è forte.
r=0	Correlazione lineare zero.
0<r<1	Correlazione positiva: più la correlazione è vicina a +1, più è forte.
r=1	Perfetta correlazione positiva.

Tieni presente che anche se esiste una relazione tra due variabili, ciò non significa che esista causalità tra di loro, ovvero la correlazione tra due variabili non significa che il cambiamento di una variabile sia la causa del cambiamento della variabile. altra variabile.

Ad esempio, se scopriamo che esiste una relazione positiva tra la produzione di due diversi ormoni nel corpo, non è necessario che l’aumento di un ormone porti ad un aumento dell’altro ormone. Potrebbe darsi che il corpo produca entrambi gli ormoni perché ne ha bisogno per combattere una malattia e quindi aumenta i livelli di entrambi contemporaneamente, nel qual caso la causa sarebbe la malattia. Per determinare se esiste un nesso causale tra i due ormoni, dovrebbero essere condotti ulteriori studi.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più