Coefficiente di correlazione intraclasse: definizione + esempio

Un coefficiente di correlazione intraclasse (ICC) viene utilizzato per misurare l’ affidabilità dei punteggi negli studi in cui sono presenti due o più valutatori.

Il valore di un ICC può variare da 0 a 1, dove 0 indica assenza di affidabilità tra i valutatori e 1 indica perfetta affidabilità tra i valutatori.

In poche parole, un ICC viene utilizzato per determinare se gli elementi (o gli argomenti) possono essere valutati in modo affidabile da valutatori diversi.

Esistono diverse versioni di un ICC che possono essere calcolate, a seconda dei seguenti tre fattori:

• Modello: effetti casuali unidirezionali, effetti casuali bidirezionali o effetti misti bidirezionali
• Tipo di rapporto: coerenza o accordo assoluto
• Unità: singolo valutatore o media dei valutatori

Ecco una breve descrizione dei tre diversi modelli :

1. Modello a effetti casuali unidirezionali: questo modello presuppone che ciascun soggetto venga valutato da un gruppo diverso di valutatori selezionati casualmente. Con questo modello, i valutatori sono considerati la fonte degli effetti casuali. Questo modello è usato raramente nella pratica perché lo stesso gruppo di valutatori viene generalmente utilizzato per valutare ciascuna materia.

2. Modello a effetti casuali a due vie: questo modello presuppone che un gruppo di valutatori k venga selezionato casualmente da una popolazione e quindi utilizzato per valutare i soggetti. Utilizzando questo modello, valutatori e soggetti sono considerati fonti di effetti casuali. Questo modello viene spesso utilizzato quando vogliamo generalizzare i nostri risultati a valutatori simili a quelli utilizzati nello studio.

3. Modello a effetti misti a due vie: questo modello presuppone inoltre che un gruppo di valutatori k venga selezionato casualmente da una popolazione e quindi utilizzato per valutare i soggetti. Tuttavia, questo modello presuppone che il gruppo di valutatori che abbiamo scelto siano gli unici valutatori di interesse, il che significa che non desideriamo generalizzare i nostri risultati ad altri valutatori che potrebbero condividere caratteristiche simili ai valutatori utilizzati nello studio.

Ecco una breve descrizione dei due diversi tipi di relazioni che potremmo voler misurare:

1. Coerenza: siamo interessati alle differenze sistematiche tra le valutazioni dei giudici (ad esempio, i giudici hanno valutato argomenti simili come bassi e alti?)

2. Accordo assoluto: siamo interessati alle differenze assolute tra i punteggi dei giudici (ad esempio, qual è la differenza assoluta tra i punteggi del giudice A e del giudice B?)

Ecco una breve descrizione delle due diverse unità che potrebbero interessarci:

1. Singolo revisore: desideriamo utilizzare le valutazioni di un singolo revisore come base per la misurazione.

2. Media dei valutatori: vogliamo utilizzare la media dei punteggi di tutti i giudici come base per la misurazione.

Nota: se desideri misurare il livello di accordo tra due valutatori che mancano ciascuno degli elementi su un risultato dicotomico , dovresti utilizzare invece il Kappa di Cohen .

Come interpretare il coefficiente di correlazione intraclasse

Ecco come interpretare il valore di un coefficiente di correlazione intraclasse, secondo Koo & Li :

• Meno di 0,50: scarsa affidabilità
• Tra 0,5 e 0,75: affidabilità moderata
• Tra 0,75 e 0,9: buona affidabilità
• Maggiore di 0,9: affidabilità eccellente

L’esempio seguente mostra come calcolare nella pratica un coefficiente di correlazione intraclasse.

Esempio: Calcolo del coefficiente di correlazione intraclasse

Supponiamo che a quattro giudici diversi venga chiesto di valutare la qualità di 10 diversi esami di ammissione all’università. I risultati sono mostrati sotto:

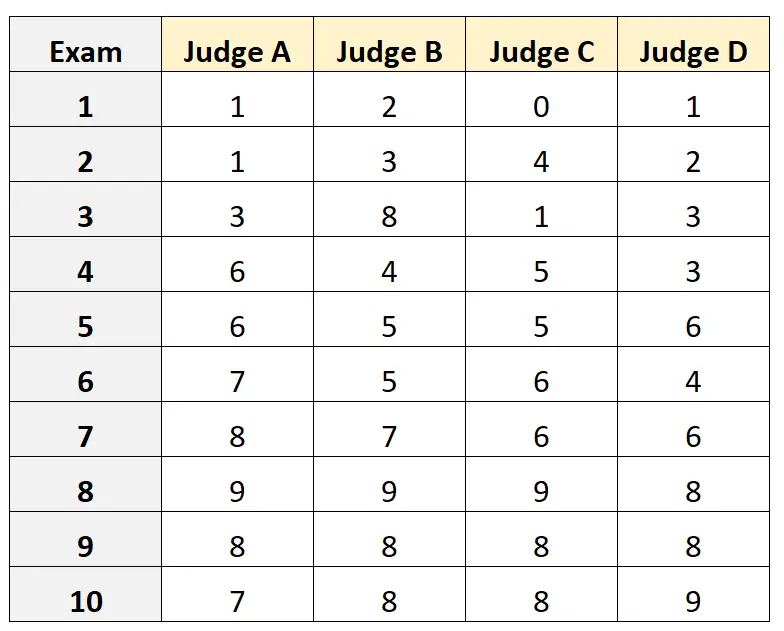
Supponiamo che i quattro giudici siano stati selezionati casualmente da una popolazione di giudici qualificati per l’esame di ammissione e di voler misurare l’accordo assoluto tra i giudici e di voler utilizzare i punteggi dal punto di vista di un solo valutatore come base della nostra misurazione.

Possiamo utilizzare il seguente codice in R per adattare un modello a effetti casuali a due vie , utilizzando l’ accordo assoluto come relazione tra i valutatori e utilizzando la singola unità come unità di interesse:

 #load the interrater reliability package
library (irr)

#define data
data <- data. frame (A=c(1, 1, 3, 6, 6, 7, 8, 9, 8, 7),
                   B=c(2, 3, 8, 4, 5, 5, 7, 9, 8, 8),
                   C=c(0, 4, 1, 5, 5, 6, 6, 9, 8, 8),
                   D=c(1, 2, 3, 3, 6, 4, 6, 8, 8, 9))

#calculate ICC
icc(data, model = " twoway ", type = " agreement ", unit = " single ")

   Model: twoway 
   Type: agreement 

   Subjects = 10 
     Failures = 4 
   ICC(A,1) = 0.782

 F-Test, H0: r0 = 0; H1: r0 > 0 
    F(9.30) = 15.3, p = 5.93e-09 

 95%-Confidence Interval for ICC Population Values:
  0.554 < ICC < 0.931

Il coefficiente di correlazione intraclasse (ICC) è risultato pari a 0,782 .

Sulla base delle regole pratiche per l’interpretazione dell’ICC, potremmo concludere che un ICC di 0,782 indica che gli esami possono essere valutati con “buona” affidabilità da valutatori diversi.

Risorse addizionali

I seguenti tutorial forniscono spiegazioni dettagliate su come calcolare l’ICC in diversi software statistici:

Come calcolare il coefficiente di correlazione intraclasse in Excel
Come calcolare il coefficiente di correlazione intraclasse in R
Come calcolare il coefficiente di correlazione intraclasse in Python