Coefficiente di determinazione (r quadrato)

Di Benjamin anderson Agosto 2, 2023 Statistiche 0 commenti

Questo articolo spiega cos’è il coefficiente di determinazione (o R quadrato) in statistica. Scoprirai quindi come calcolare il coefficiente di determinazione, come viene interpretato e, inoltre, un calcolatore online per calcolare il coefficiente di determinazione di un campione di dati.

Qual è il coefficiente di determinazione (R quadrato)?

Il coefficiente di determinazione , il cui simbolo è R ² ( R al quadrato ), è una statistica che misura la bontà di adattamento di un modello di regressione. Il coefficiente di determinazione mostra quanto bene un modello di regressione si adatta a un set di dati, ovvero indica la percentuale spiegata dal modello di regressione.

Pertanto, maggiore è il coefficiente di determinazione, migliore è il modello di regressione. Sebbene questa condizione non sia sempre soddisfatta, in linea di principio siamo interessati al coefficiente di determinazione più grande possibile. Vedremo di seguito come interpretare il coefficiente di determinazione.

Formula del coefficiente determinante

Il coefficiente di determinazione è pari a uno meno il rapporto tra la varianza residua e la varianza della variabile dipendente. Il coefficiente di determinazione può anche essere calcolato sottraendo uno meno la somma dei quadrati dai residui sulla somma totale dei quadrati.

Pertanto, la formula per calcolare il coefficiente di determinazione è la seguente:

formula per il coefficiente di determinazione, formula per r quadrato

Oro:

$R^2$

è il coefficiente di determinazione.
$\sigma_r^2$

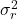
è la varianza residua.
$\sigma^2$

è la varianza della variabile dipendente Y.
$y_{i}$

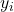
è il valore della variabile dipendente dall’osservazione i.
$\widehat{y}_{i}$

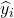
è il valore approssimato dal modello di regressione per l’osservazione i.
$\overline{y}$

è la media della variabile dipendente tra tutte le osservazioni.

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare il coefficiente di determinazione per qualsiasi set di dati.

Nel caso del modello di regressione lineare, il coefficiente di determinazione è equivalente al quadrato del coefficiente di correlazione :

$R^2=\cfrac{\sigma_{XY}^2}{\sigma_X^2\sigma_Y^2}=\rho^2$

Oro

$\sigma_{XY}^2$

è la covarianza delle variabili X e Y,

$\sigma_X^2$

$\sigma_Y^2$

sono le varianze rispettivamente della variabile indipendente X e della variabile dipendente Y.

Calcolatore del coefficiente di determinazione

Inserisci un campione di dati nel calcolatore sottostante per adattare un semplice modello di regressione lineare e calcolarne il coefficiente di determinazione. È necessario separare le coppie di dati, in modo che nella prima casella ci siano solo i valori della variabile indipendente X e nella seconda casella ci siano solo i valori della variabile dipendente Y.

I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Interpretazione del coefficiente di determinazione

In questa sezione vedremo come interpretare il coefficiente di determinazione, perché non ha senso conoscere il valore del coefficiente di determinazione se non si sa poi cosa significa.

Il valore del coefficiente di determinazione può variare da 0 a 1, tuttavia solitamente è espresso in percentuale, quindi il minimo è 0% e il massimo è 100%.

Per quanto riguarda l’ interpretazione del coefficiente di determinazione , maggiore è il suo valore significa che il modello di regressione spiega meglio il campione di dati. Pertanto, quanto più il coefficiente di determinazione si avvicina a 1, tanto più il modello verrà aggiustato. D’altra parte, quanto più si avvicina allo 0, tanto meno affidabile sarà il modello di regressione prodotto.

Tuttavia, quando si confrontano due modelli di regressione, il modello con un coefficiente di regressione più elevato non è sempre migliore. Ad esempio, un modello di regressione può avere un coefficiente di regressione R ² = 100% perché al modello sono state aggiunte molte variabili esplicative e, quindi, può spiegare perfettamente tutte le osservazioni. Ma questo modello fornisce sicuramente una previsione molto inadeguata per un nuovo valore che non è stato utilizzato per costruire il modello di regressione.

Va inoltre tenuto presente che il modello di regressione risultante soddisfa le ipotesi precedenti. Pertanto, un modello con un coefficiente di determinazione molto elevato è inutile se la variabilità dei suoi residui non è costante (omoschedasticità).

Inoltre, il coefficiente di determinazione presenta un limite importante, poiché non penalizza l’inclusione di variabili esplicative. Logicamente, più variabili esplicative ha un modello di regressione, più il modello sarà complesso, ma meglio spiegherà i dati osservati e, quindi, più alto sarà il coefficiente di determinazione. Tuttavia, il coefficiente di determinazione corretto tiene conto del numero di variabili presenti nel modello (vedremo di seguito come viene calcolato).

In conclusione, il coefficiente di determinazione è molto utile per analizzare un modello di regressione perché ci consente di sapere quanto bene il modello di regressione si adatta al set di dati. Tuttavia, per rivedere il modello risultante dovrebbero essere utilizzati anche altri strumenti, come i grafici statistici .

Coefficiente di determinazione rettificato

Il coefficiente di determinazione corretto , chiamato anche coefficiente di determinazione corretto , misura la bontà di adattamento di un modello di regressione tenendo conto del numero di variabili esplicative incluse nel modello.

La differenza tra il coefficiente di determinazione e il coefficiente di determinazione corretto è che il coefficiente di determinazione misura la qualità dell’aggiustamento senza tenere conto del numero di variabili, d’altra parte, il coefficiente di determinazione corretto misura la qualità dell’aggiustamento penalizzante per ogni variabile aggiunta.

La formula per il calcolo del coefficiente di determinazione corretto è la seguente:

$\bar{R}^2=1-\cfrac{N-1}{N-k-1}\cdot (1-R^2)$

Oro:

$\bar{R}^2$

è il coefficiente di determinazione corretto.
$R^2$

è il coefficiente di determinazione.
$N$

è la dimensione del campione.
$k$

è il numero di variabili esplicative nel modello di regressione.

Pertanto, il coefficiente di determinazione corretto è migliore del coefficiente di determinazione per confrontare due modelli diversi, poiché i modelli possono avere un numero diverso di variabili esplicative.

➤ Vedi: Coefficiente di determinazione rettificato

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più