Coefficiente phi: definizione ed esempi

Un coefficiente Phi (a volte chiamato coefficiente di contingenza quadratico medio ) è una misura dell’associazione tra due variabili binarie.

Per una tabella 2×2 data per due variabili casuali x e y :

Il coefficiente Phi può essere calcolato come segue:

Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)

Esempio: Calcolo di un coefficiente Phi

Supponiamo di voler sapere se il genere è associato o meno alla preferenza per un partito politico. Prendiamo un semplice campione casuale di 25 elettori e chiediamo loro quale sia la loro preferenza per il partito politico. La tabella seguente presenta i risultati dell’indagine:

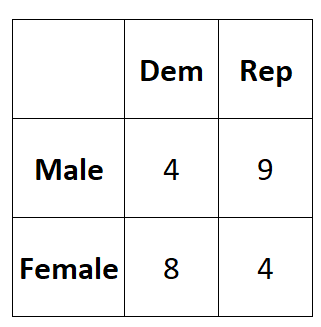
Possiamo calcolare il coefficiente Phi tra le due variabili come segue:

Φ = (4*4-9*8) / √ (4+9)(8+4)(4+8)(9+4) = (16-72) / √ 24336 = -0,3589

Nota: avremmo potuto calcolarlo anche utilizzando il calcolatore del coefficiente Phi.

Come interpretare un coefficiente Phi

Similmente al coefficiente di correlazione di Pearson, il coefficiente Phi assume valori compresi tra -1 e 1 dove:

• -1 indica una relazione perfettamente negativa tra le due variabili.
• 0 indica nessuna associazione tra le due variabili.
• 1 indica una relazione perfettamente positiva tra le due variabili.

In generale, più un coefficiente Phi è lontano da zero, più forte è la relazione tra le due variabili.

In altre parole, più un coefficiente Phi è lontano da zero, maggiore è la prova di un qualche tipo di modello sistematico tra le due variabili.

Risorse addizionali

Una guida al coefficiente di correlazione di Pearson
Una guida al test esatto di Fisher
Una guida al test di indipendenza del chi quadrato