Come calcolare un coefficiente phi in r

Un coefficiente Phi (a volte chiamato coefficiente di contingenza quadratico medio ) è una misura dell’associazione tra due variabili binarie.

Per una tabella 2×2 data per due variabili casuali x e y :

Il coefficiente Phi può essere calcolato come segue:

Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)

Esempio: calcolo di un coefficiente Phi in R

Supponiamo di voler sapere se il genere è associato o meno alla preferenza per un partito politico. Quindi prendiamo un semplice campione casuale di 25 elettori e chiediamo loro quale sia la loro preferenza per un partito politico.

La tabella seguente presenta i risultati dell’indagine:

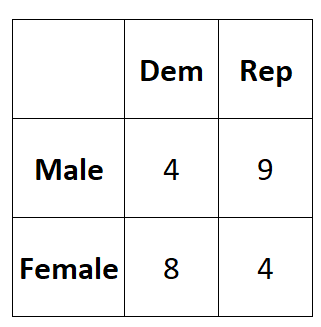
Possiamo usare il seguente codice per inserire questi dati in una matrice 2×2 in R:

 #create 2x2 table
data = matrix(c(4, 8, 9, 4), nrow = 2 )

#view dataset
data

     [,1] [,2]
[1,] 4 9
[2,] 8 4

Possiamo quindi utilizzare la funzione phi() del pacchetto psych per calcolare il coefficiente Phi tra le due variabili:

 #load psych package
library (psych)

#calculate Phi Coefficient
phi(data)

[1] -0.36

Il coefficiente Phi risulta essere -0,36 .

Tieni presente che la funzione phi arrotonda a 2 cifre per impostazione predefinita, ma puoi specificare che la funzione arrotonda a tutte le cifre che desideri:

 #calculate Phi Coefficient and round to 6 digits
phi(data, digits = 6 )

[1] -0.358974

Come interpretare un coefficiente Phi

Similmente al coefficiente di correlazione di Pearson, il coefficiente Phi assume valori compresi tra -1 e 1 dove:

• -1 indica una relazione perfettamente negativa tra le due variabili.
• 0 indica nessuna associazione tra le due variabili.
• 1 indica una relazione perfettamente positiva tra le due variabili.

In generale, più un coefficiente Phi è lontano da zero, più forte è la relazione tra le due variabili.

In altre parole, più un coefficiente Phi è lontano da zero, maggiore è la prova di un qualche tipo di modello sistematico tra le due variabili.

Risorse addizionali

Un’introduzione al coefficiente Phi
Calcolatore del coefficiente Phi