Come calcolare la d di cohen in excel

In statistica, quando vogliamo determinare se esiste o meno una differenza significativa tra due gruppi, spesso eseguiamo un test di ipotesi, che risulta in un valore p .

Se questo valore p è inferiore a un certo livello di significatività (le scelte comuni sono 0,10, 0,05 e 0,01), concludiamo che esiste una differenza statisticamente significativa tra i due gruppi.

Tuttavia, mentre il valore p può dirci se esiste o meno una differenza statisticamente significativa tra due gruppi, la dimensione dell’effetto può dirci quanto è realmente grande tale differenza.

Una delle misure più comuni della dimensione dell’effetto è la d di Cohen , che viene calcolata come segue:

d di Cohen = ( x ₁ – x ₂ ) / SD aggregata

Oro:

• x ₁ = media del gruppo 1
• x ₂ = media del gruppo 2
• SD raggruppato = √ (s ₁ ² + s ₂ ² ) / 2

Questo tutorial spiega come calcolare la d di Cohen in Excel.

Esempio: d di Cohen in Excel

Completa i seguenti passaggi per calcolare la d di Cohen in Excel.

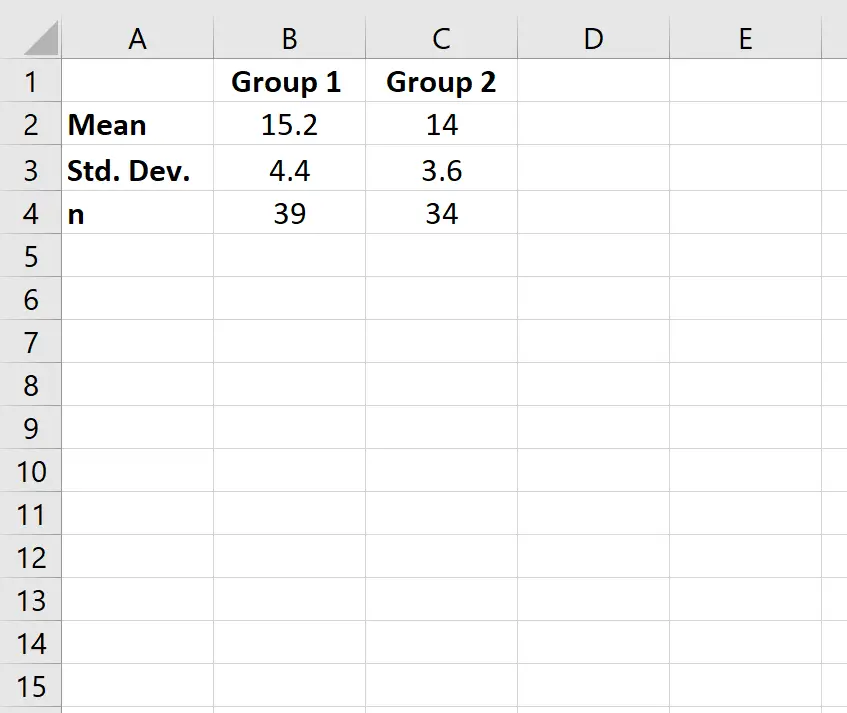
Passaggio 1: inserisci i dati.

Innanzitutto, inseriremo i valori della media, della deviazione standard e della dimensione del campione (n) per due gruppi.

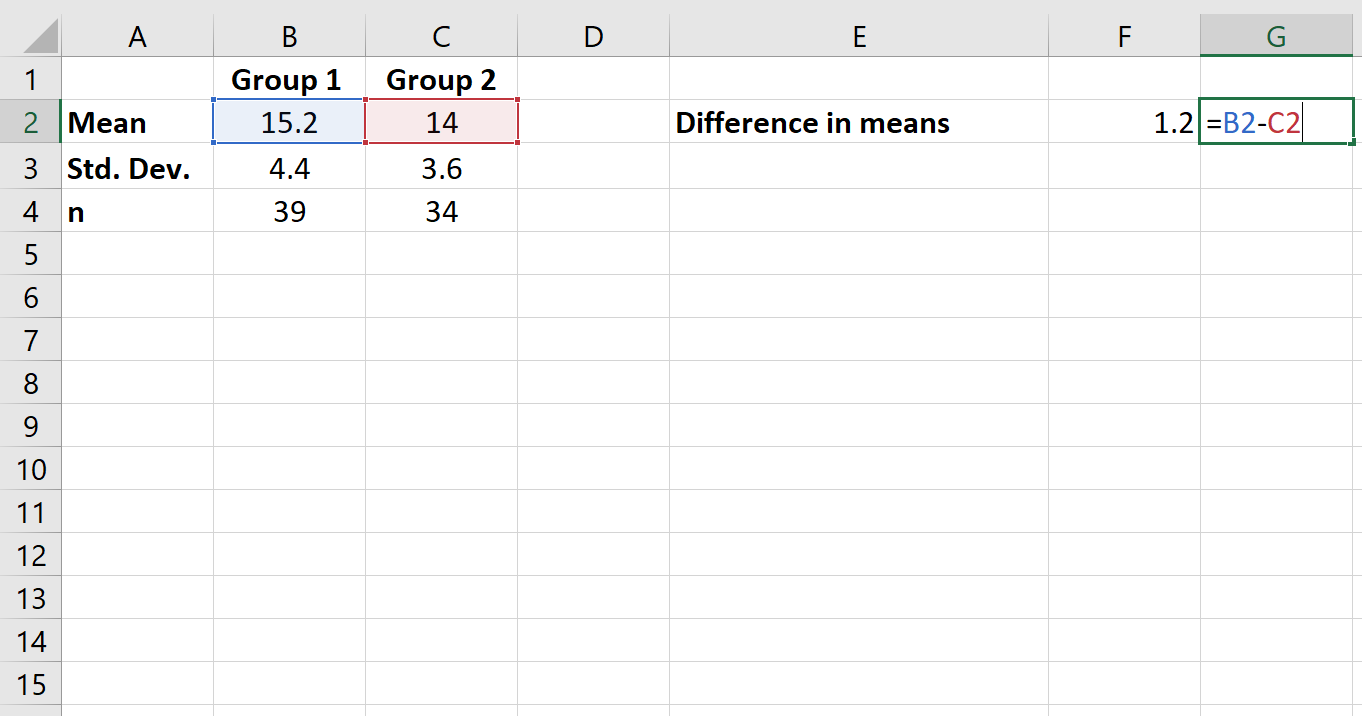
Passaggio 2: calcolare la differenza nelle medie.

Successivamente, calcoleremo la differenza tra le medie del gruppo.

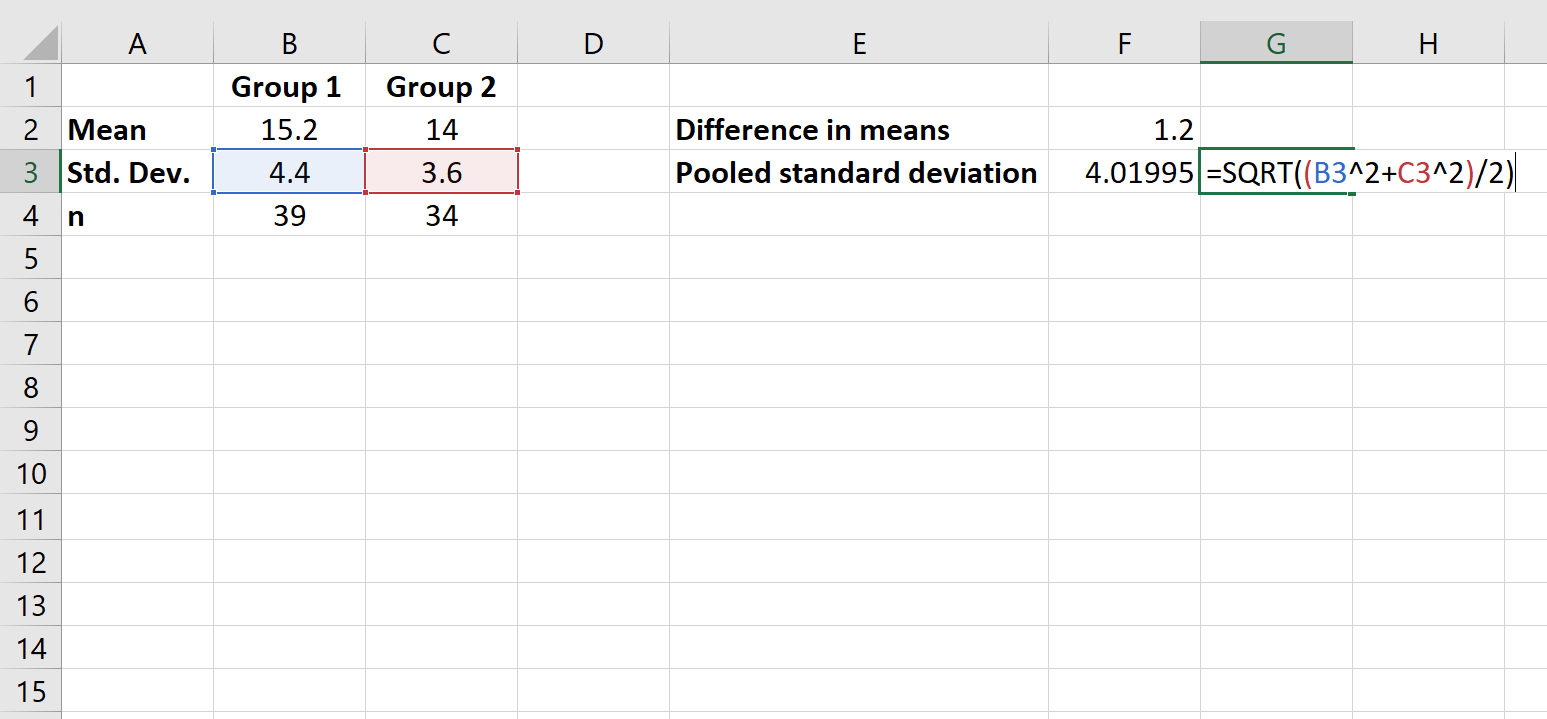
Passaggio 3: calcolare la deviazione standard aggregata.

Successivamente, calcoleremo la deviazione standard aggregata.

Passaggio 4: calcolare il d di Cohen.

Infine, calcoleremo il d di Cohen.

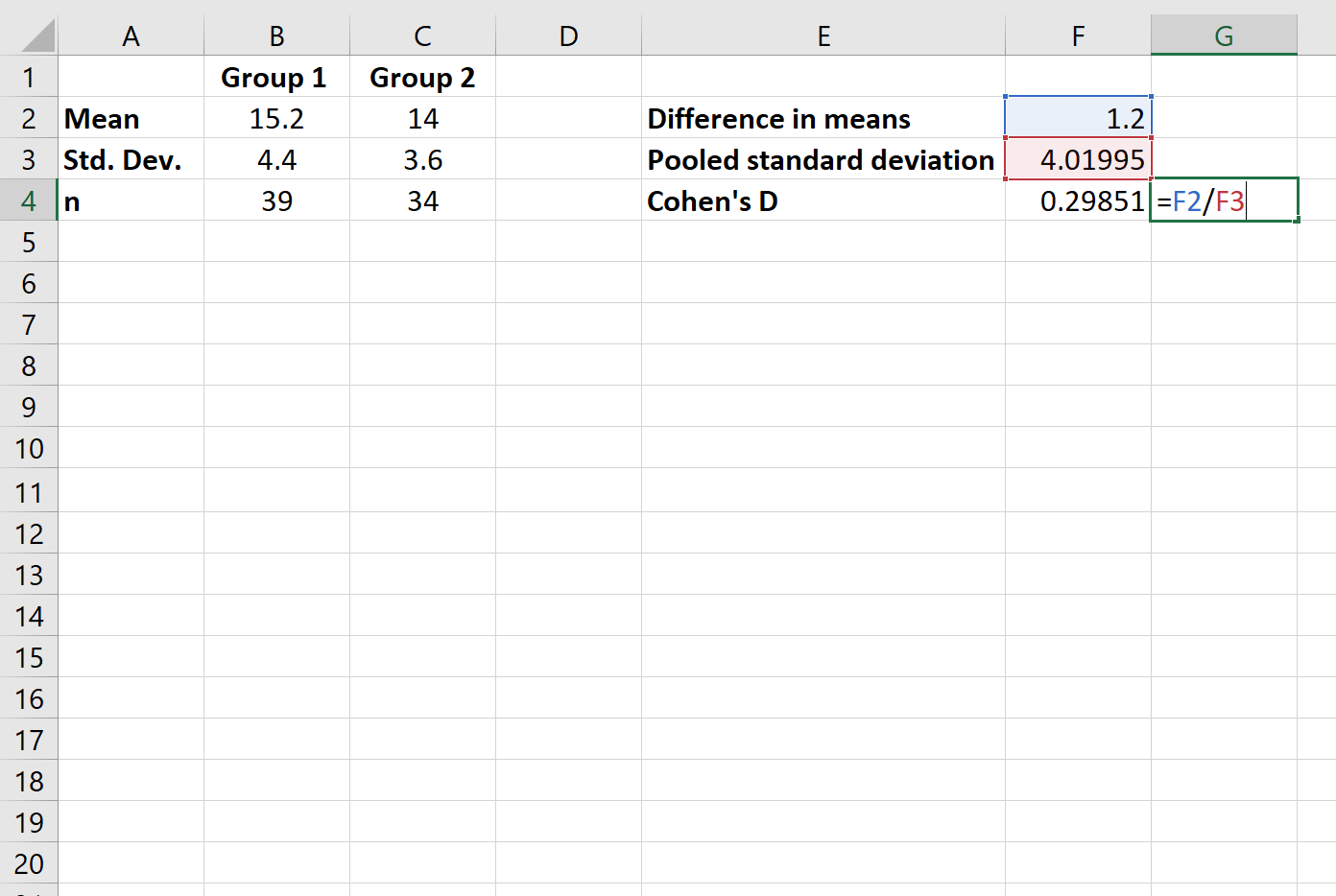
Per questo esempio la d di Cohen risulta essere 0,29851 .

Come interpretare il d

Come regola generale, ecco come interpretare la d di Cohen:

• 0,2 = dimensione dell’effetto piccola
• 0,5 = dimensione dell’effetto media
• 0,8 = dimensione dell’effetto grande

Nel nostro esempio, una dimensione dell’effetto pari a 0,29851 sarebbe probabilmente considerata una dimensione dell’effetto piccola.

Ciò significa che anche se la differenza tra le medie dei due gruppi è statisticamente significativa, la differenza effettiva tra le medie dei due gruppi è insignificante.