Come calcolare sxx in statistica (con esempio)

In statistica, Sxx rappresenta la somma dei quadrati delle deviazioni dal valore medio di x.

Questo valore viene spesso calcolato durante l’adattamento manuale di un semplice modello di regressione lineare .

Usiamo la seguente formula per calcolare Sxx:

Sxx = Σ( _xi – x ) ²

Oro:

• Σ : Un simbolo che significa “somma”
• x _i : l’ ^i-esimo valore di x
• x : il valore medio di x

L’esempio seguente mostra come utilizzare questa formula nella pratica.

Esempio: calcolare Sxx a mano

Supponiamo di voler adattare un modello di regressione lineare semplice al seguente set di dati:

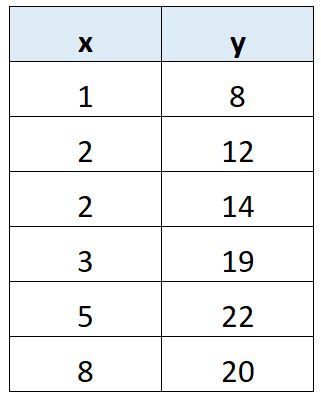
Supponiamo di voler calcolare Sxx, che rappresenta la somma dei quadrati delle deviazioni dal valore medio di x.

Innanzitutto dobbiamo calcolare il valore medio di x:

• x = (1 + 2 + 2 + 3 + 5 + 8) / 6 = 3,5

Quindi possiamo utilizzare la seguente formula per calcolare il valore di Sxx:

• Sxx = Σ( _xi – x ) ²
• Sxx = (1-3,5) ² +(2-3,5) ² +(2-3,5) ² +(3-3,5) ² +(5-3,5) ² +(8- 3,5) ²
• Sxx = 6,25 + 2,25 + 2,25 + 0,25 + 2,25 + 20,25
• Sxx = 33,5

Il valore di Sxx risulta essere 33,5 .

Questo ci dice che la somma dei quadrati degli scostamenti tra i singoli valori di x e il valore medio di x è 33,5.

Tieni presente che potremmo anche utilizzare il calcolatore Sxx per calcolare automaticamente il valore di Sxx per questo modello:

La calcolatrice restituisce un valore di 33,5 , che è il valore calcolato manualmente.

Tieni presente che utilizziamo le seguenti formule per eseguire manualmente una regressione lineare semplice:

y = a + bx

Oro:

• a = y – bx
• b = Sxy/Sxx

Il calcolo per Sxx è solo un calcolo che dobbiamo eseguire per adattare un semplice modello di regressione lineare.

Correlati: Come calcolare Sxy nelle statistiche

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni nelle statistiche:

Come eseguire manualmente una semplice regressione lineare
Come eseguire manualmente la regressione lineare multipla