Come calcolare sxy in statistica (con esempio)

In statistica, Sxy rappresenta la somma del prodotto delle differenze tra i valori di x e la media di x e delle differenze tra i valori di y e la media di y.

Questo valore viene spesso calcolato durante l’adattamento manuale di un semplice modello di regressione lineare .

Usiamo la seguente formula per calcolare Sxy:

Sxy = Σ(x _i – x )(y _i – y )

Oro:

• Σ : Un simbolo che significa “somma”
• x _i : l’ ^i-esimo valore di x
• x : il valore medio di x
• y _i : l’i ^-esimo valore di y
• y : il valore medio di y

L’esempio seguente mostra come utilizzare questa formula nella pratica.

Esempio: Calcola Sxy a mano

Supponiamo di voler adattare un modello di regressione lineare semplice al seguente set di dati:

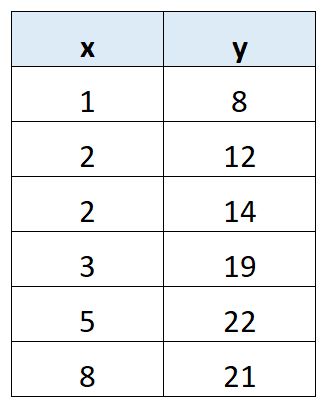
Supponiamo di voler calcolare Sxy per questo set di dati.

Innanzitutto dobbiamo calcolare il valore medio di x:

• x = (1 + 2 + 2 + 3 + 5 + 8) / 6 = 3,5

Quindi, dobbiamo calcolare il valore medio di y:

• y = (8 + 12 + 14 + 19 + 22 + 21) / 6 = 16

Utilizzando questi valori, la schermata seguente mostra come calcolare il valore di Sxy:

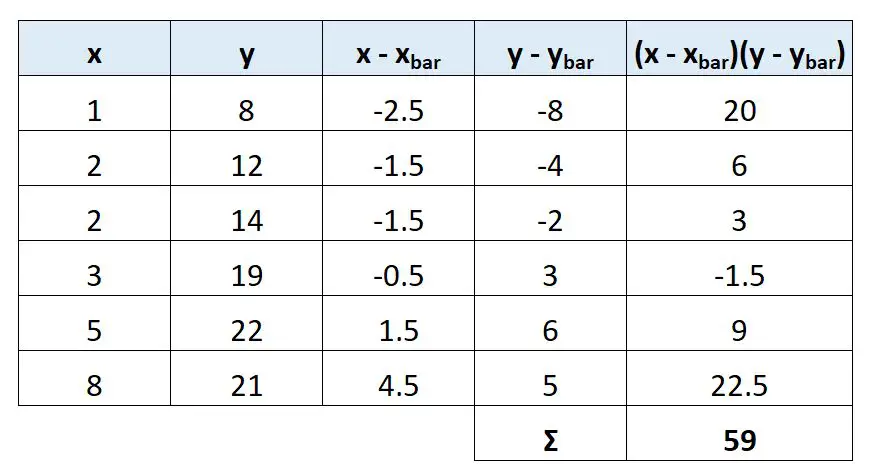
Il valore di Sxy risulta essere 59 .

Tieni presente che potremmo anche utilizzare il calcolatore Sxy per calcolare automaticamente il valore di Sxy per questo modello:

La calcolatrice restituisce un valore di 59 , che è il valore calcolato manualmente.

Tieni presente che utilizziamo le seguenti formule per eseguire manualmente una regressione lineare semplice:

y = a + bx

Oro:

• a = y – bx
• b = Sxy/Sxx

Il calcolo per Sxy è solo un calcolo che dobbiamo eseguire per adattare un semplice modello di regressione lineare.

Correlato: Come calcolare Sxx in statistica

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni nelle statistiche:

Come eseguire manualmente una semplice regressione lineare
Come eseguire manualmente la regressione lineare multipla