Come calcolare manualmente un valore p da un test t

Uno dei test più comunemente utilizzati in statistica è il test t , che viene spesso utilizzato per determinare se la media di una popolazione equivale a un determinato valore.

Ad esempio, supponiamo di voler sapere se l’altezza media di una determinata specie di piante è pari a 15 pollici. Per testarlo, potremmo raccogliere un campione casuale di 20 piante, trovare la media del campione e la deviazione standard del campione ed eseguire un test t per determinare se l’altezza media è effettivamente di 15 pollici.

Le ipotesi nulla e alternativa del test sono le seguenti:

_H0 : µ = 15

H _a : µ ≠ 15

La formula per la statistica del test è:

t = ( X -μ) / (s/ √n )

dove x è la media campionaria, μ è la media ipotetica (nel nostro esempio sarebbe 15), s è la deviazione standard del campione e n è la dimensione del campione.

Una volta conosciuto il valore di t , possiamo utilizzare un software statistico o un calcolatore online per trovare il valore p corrispondente. Se il valore p è inferiore a un certo livello alfa (le scelte comuni sono 0,01, 0,05 e 0,10), allora possiamo rifiutare l’ipotesi nulla e concludere che l’altezza media della pianta non è uguale a 15 pollici.

Tuttavia, è anche possibile stimare manualmente il valore p del test utilizzando una tabella di distribuzione t . In questo articolo spiegheremo come farlo.

Esempio: calcolo manuale del valore p da un test t

Problema : Bob vuole sapere se l’altezza media di una certa specie di pianta è pari a 15 pollici. Per verificarlo, raccoglie un campione casuale di 20 piante e scopre che la media del campione è di 14 pollici e la deviazione standard del campione è di 3 pollici. Esegui un test t utilizzando un livello alfa di 0,05 per determinare se l’altezza media reale della popolazione è effettivamente di 15 pollici.

Soluzione:

Passaggio 1: enunciare le ipotesi nulla e alternativa.

_H0 : µ = 15

H _a : µ ≠ 15

Passaggio 2: trova la statistica del test.

t = ( x -μ) / (s/ √n ) = (14-15) / (3/ √20 ) = -1,49

Passaggio 3: trovare il valore p per la statistica del test.

Per trovare manualmente il valore p, dobbiamo utilizzare la tabella di distribuzione t con n-1 gradi di libertà. Nel nostro esempio, la dimensione del campione è n = 20, quindi n-1 = 19.

Nella tabella della distribuzione t qui sotto, dobbiamo guardare la riga che corrisponde a “19” sul lato sinistro e tentare di trovare il valore assoluto della nostra statistica di test 1,49 .

Da notare che 1.49 non compare nella tabella, ma rientra tra i due valori 1.328 e 1.729 .

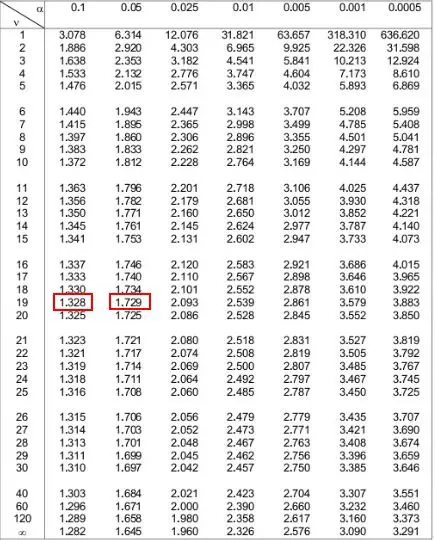
Quindi possiamo osservare i due livelli alfa nella parte superiore della tabella che corrispondono a questi due numeri. Vediamo che sono 0.1 e 0.05 .

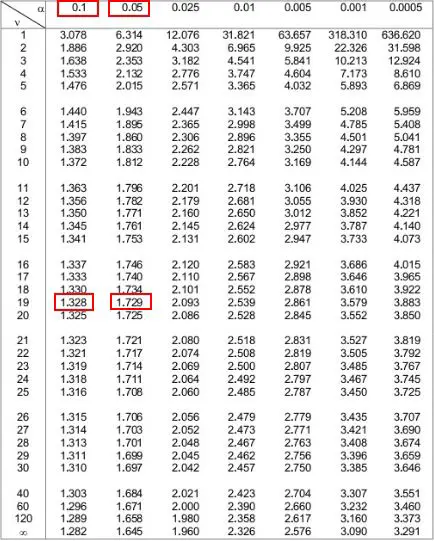
Ciò significa che il valore p per un test a una coda è compreso tra 0,1 e 0,05. Chiamiamolo .075. Poiché il nostro test t è a due code, dobbiamo moltiplicare questo valore per 2. Pertanto, il nostro valore p stimato è 0,075 * 2 = 0,15 .

Passaggio 4: trarre una conclusione.

Poiché questo valore p non è inferiore al livello alfa scelto di 0,05, non possiamo rifiutare l’ipotesi nulla. Pertanto, non abbiamo prove sufficienti per affermare che la vera altezza media di questa specie di pianta sia diversa da 15 pollici.

Controlla i risultati con una calcolatrice

Possiamo inserire la statistica del test t e i gradi di libertà in un calcolatore del valore p online per vedere quanto il nostro valore p stimato fosse vicino al valore p reale:

Il vero valore p è 0.15264 , che è abbastanza vicino al nostro valore p stimato di 0.15 .

Conclusione

Abbiamo visto in questo articolo che è possibile stimare manualmente il valore p di un test t utilizzando la tabella di distribuzione t. Tuttavia, nella maggior parte degli scenari non dovrai mai calcolare il valore p a mano e puoi utilizzare software statistici come R ed Excel o un calcolatore online per trovare l’esatto valore p del test.

Nella maggior parte dei casi, soprattutto in studi ed esperimenti statistici rigorosi, ti consigliamo di utilizzare una calcolatrice per trovare l’esatto valore p da un test t per essere il più preciso possibile, ma è bene sapere che puoi sempre stimare manualmente il valore p valore p da un test t se è assolutamente necessario.