Come calcolare vif in excel

La multicollinearità nell’analisi di regressione si verifica quando due o più variabili esplicative sono altamente correlate tra loro, in modo tale da non fornire informazioni univoche o indipendenti nel modello di regressione. Se il grado di correlazione tra le variabili è sufficientemente elevato, ciò può causare problemi durante l’adattamento e l’interpretazione del modello di regressione.

Fortunatamente, è possibile rilevare la multicollinearità utilizzando una metrica chiamata fattore di inflazione della varianza (VIF) , che misura la correlazione e la forza della correlazione tra le variabili esplicative in un modello di regressione.

Questo tutorial spiega come calcolare VIF in Excel.

Esempio: calcolo del VIF in Excel

Per questo esempio, eseguiremo una regressione lineare multipla utilizzando il seguente set di dati che descrive gli attributi di 10 giocatori di basket. Adatteremo un modello di regressione utilizzando il rating come variabile di risposta e punti, assist e rimbalzi come variabili esplicative. Successivamente, identificheremo i valori VIF per ciascuna variabile esplicativa.

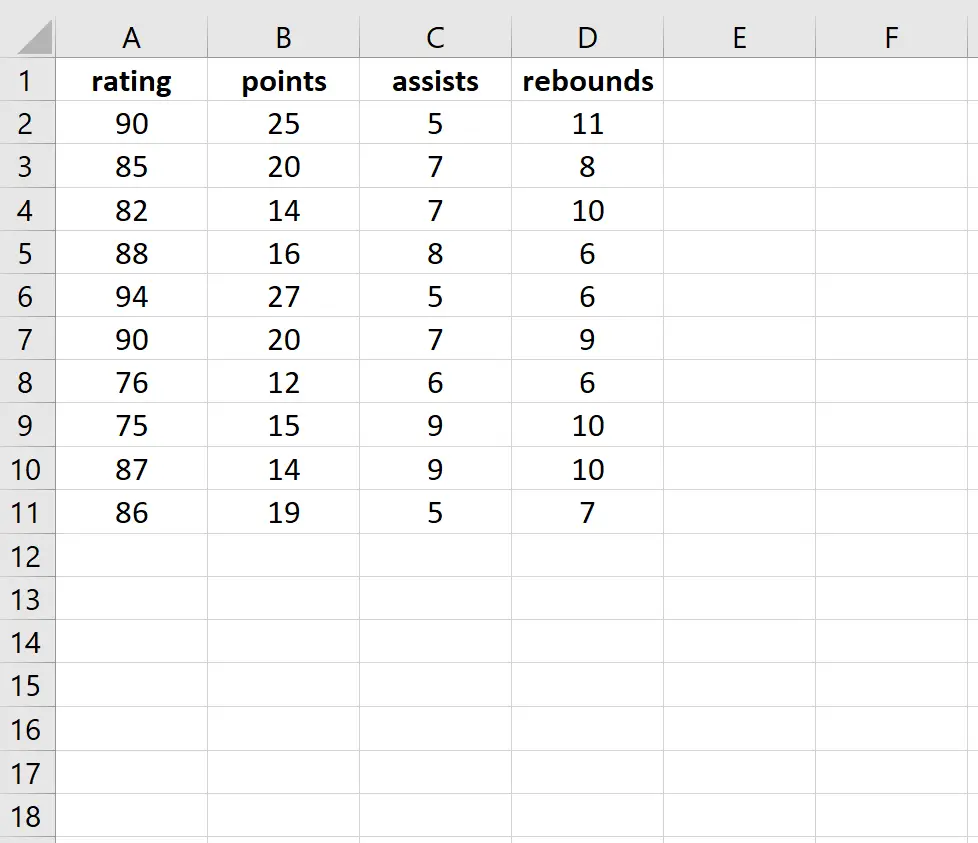
Passaggio 1: eseguire la regressione lineare multipla.

Sulla barra multifunzione in alto, vai alla scheda Dati e fai clic su Analisi dati. Se non vedi questa opzione, devi prima installare il software gratuito Analysis ToolPak .

Dopo aver fatto clic su Analisi dati, verrà visualizzata una nuova finestra. Selezionare Regressione e fare clic su OK.

Completare le tabelle necessarie per le variabili di risposta e le variabili esplicative, quindi fare clic su OK.

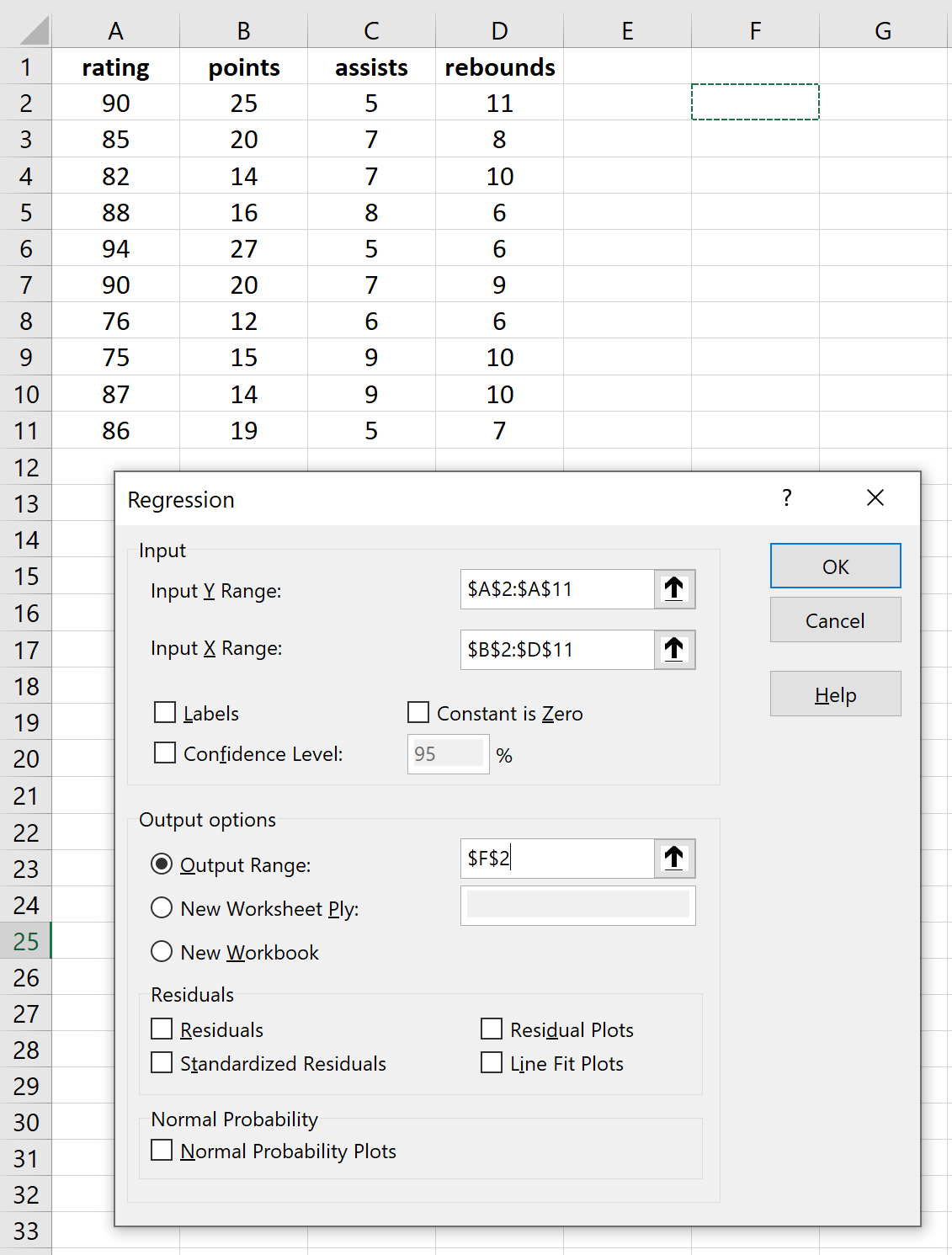
Ciò produce il seguente risultato:

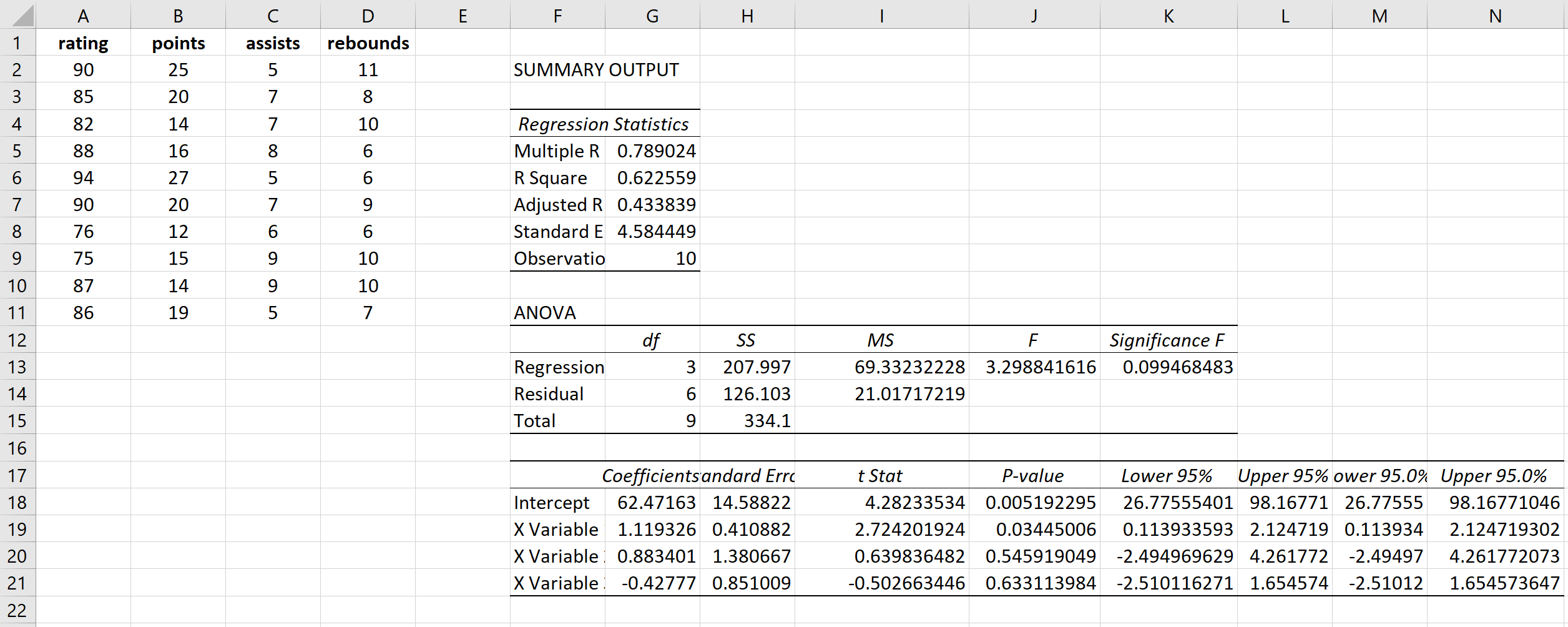
Passaggio 2: calcolare il VIF per ciascuna variabile esplicativa.

Successivamente, possiamo calcolare il VIF per ciascuna delle tre variabili esplicative eseguendo regressioni individuali utilizzando una variabile esplicativa come variabile di risposta e le altre due come variabili esplicative.

Ad esempio, possiamo calcolare il VIF per la variabile punti eseguendo una regressione lineare multipla utilizzando i punti come variabile di risposta e gli aiuti e i rimbalzi come variabili esplicative.

Ciò produce il seguente risultato:

Il VIF per i punti è calcolato come 1 / (1 – R quadrato) = 1 / (1 – .433099) = 1,76 .

Possiamo quindi ripetere questo processo per le altre due variabili, assist e rimbalzi .

Risulta che i VIF per le tre variabili esplicative sono i seguenti:

punti: 1,76
assist: 1,96
rimbalzi: 1.18

Come interpretare i valori VIF

Il valore VIF inizia da 1 e non ha un limite superiore. Una regola generale per interpretare i VIF è:

• Un valore pari a 1 indica che non esiste alcuna correlazione tra una determinata variabile esplicativa e qualsiasi altra variabile esplicativa nel modello.
• Un valore compreso tra 1 e 5 indica una correlazione moderata tra una determinata variabile esplicativa e altre variabili esplicative nel modello, ma spesso non è abbastanza grave da richiedere un’attenzione speciale.
• Un valore maggiore di 5 indica una correlazione potenzialmente grave tra una determinata variabile esplicativa e altre variabili esplicative nel modello. In questo caso, le stime dei coefficienti e i valori p nei risultati della regressione sono probabilmente inaffidabili.

Poiché ciascuno dei valori VIF delle variabili esplicative nel nostro modello di regressione è chiuso a 1, la multicollinearità non è un problema nel nostro esempio.