Come eseguire un test u di mann-whitney in excel

Un test U di Mann-Whitney (a volte chiamato test della somma dei ranghi di Wilcoxon) viene utilizzato per confrontare le differenze tra due campioni quando le distribuzioni dei campioni non sono distribuite normalmente e le dimensioni del campione sono piccole (n < 30).

È considerato l’equivalente non parametrico del test t a due campioni .

Questo tutorial spiega come eseguire un test U di Mann-Whitney in Excel.

Esempio: test U di Mann-Whitney in Excel

I ricercatori vogliono sapere se il trattamento del carburante provoca un cambiamento nel consumo medio di un’auto. Per verificarlo, conducono un esperimento in cui misurano il consumo di mpg di 12 auto con trattamento del carburante e 12 auto senza trattamento.

Poiché le dimensioni del campione sono piccole e si sospetta che le distribuzioni del campione non siano distribuite normalmente, hanno deciso di eseguire un test U di Mann-Whitney per determinare se esiste una differenza statisticamente significativa in mpg tra i due gruppi.

Completa i passaggi seguenti per eseguire un test U di Mann-Whitney in Excel.

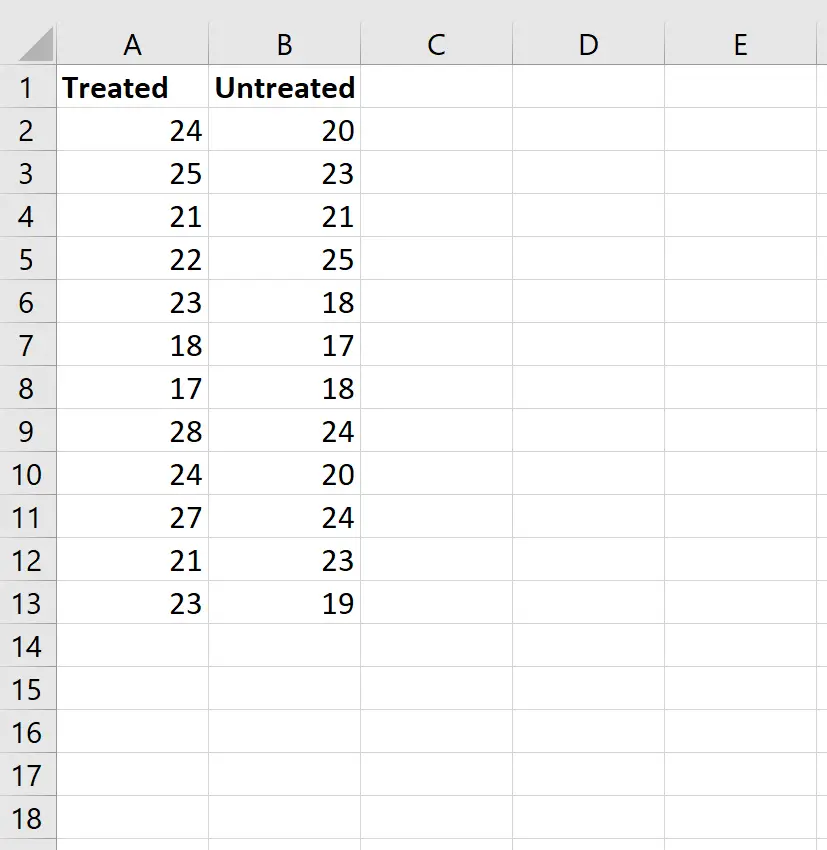
Passaggio 1: inserisci i dati.

Inserisci i dati come segue:

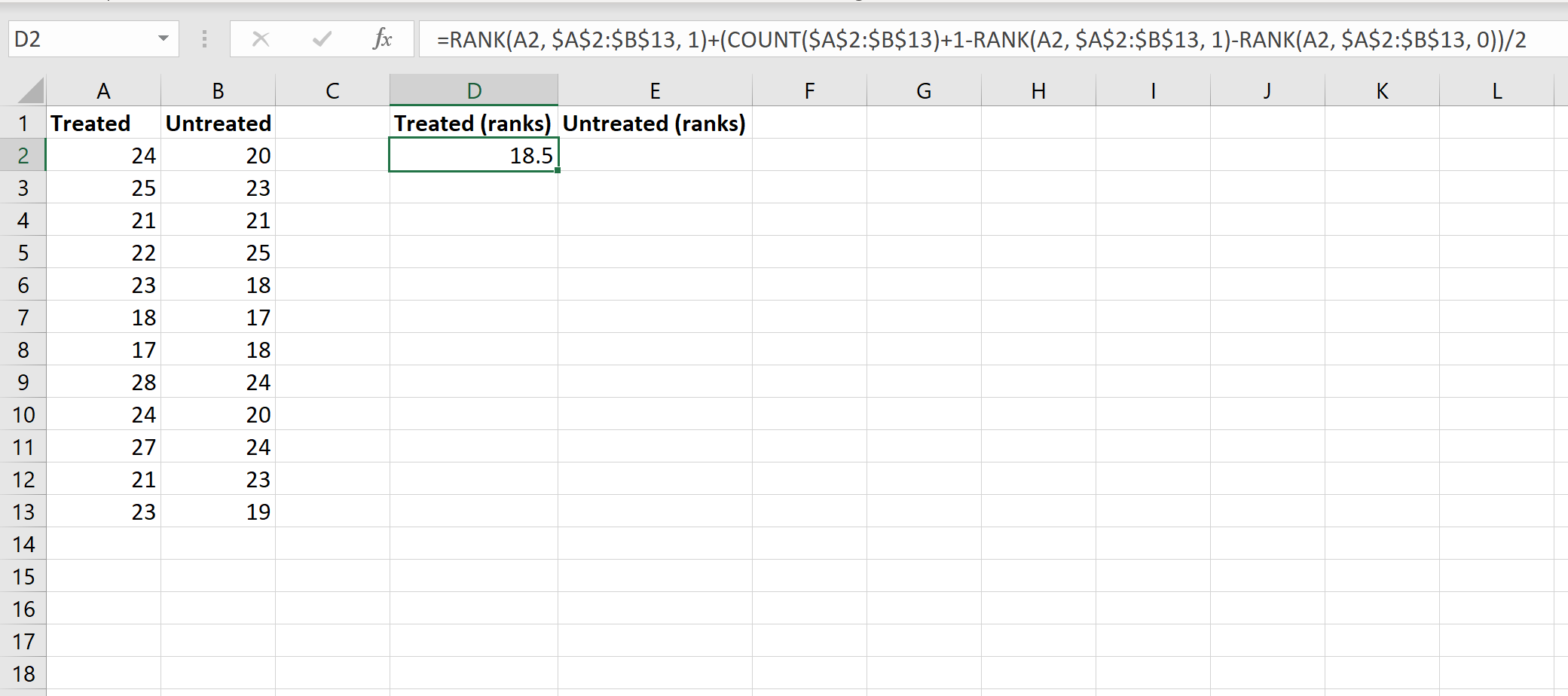
Passaggio 2: calcolare le classifiche per entrambi i gruppi.

Successivamente calcoleremo la classifica per ogni girone. L’immagine seguente mostra la formula da utilizzare per calcolare il rango del primo valore nel gruppo Elaborati:

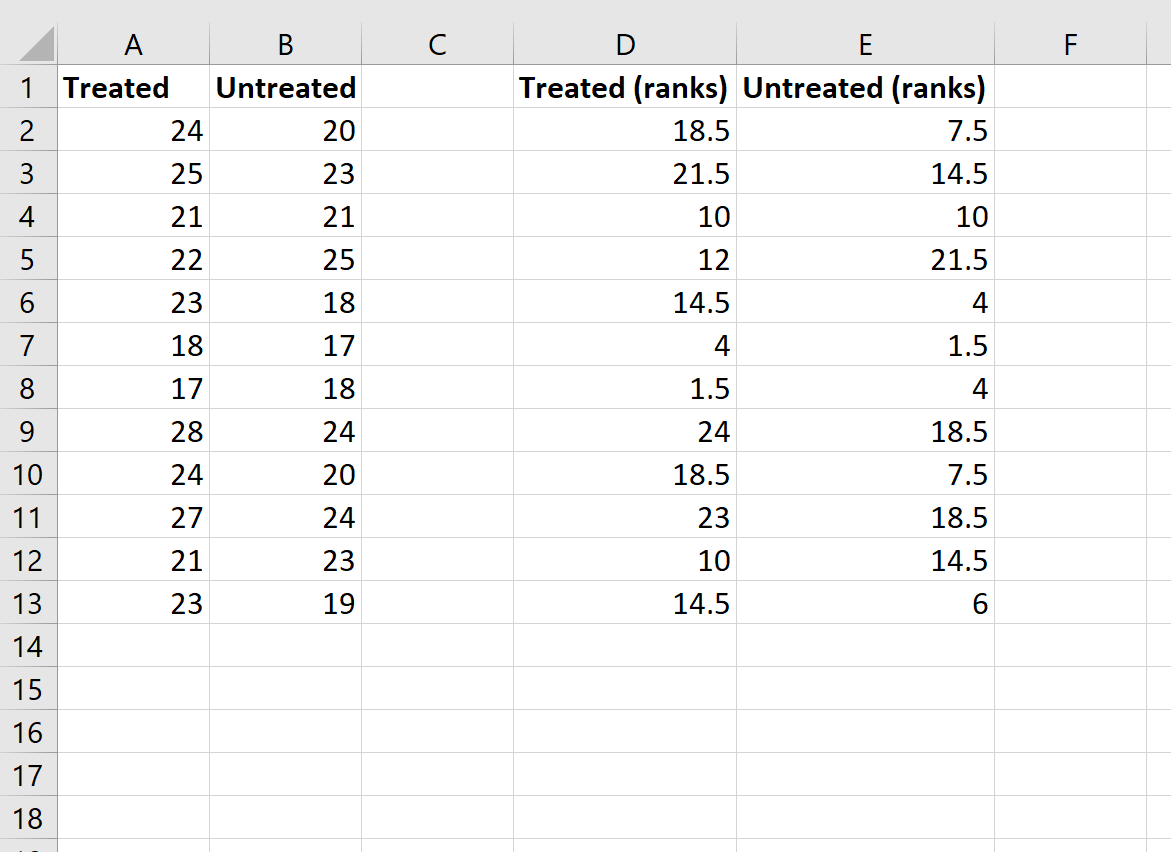
Sebbene questa formula sia piuttosto complicata, devi inserirla solo una volta. Quindi puoi semplicemente trascinare la formula su tutte le altre celle per riempire le righe:

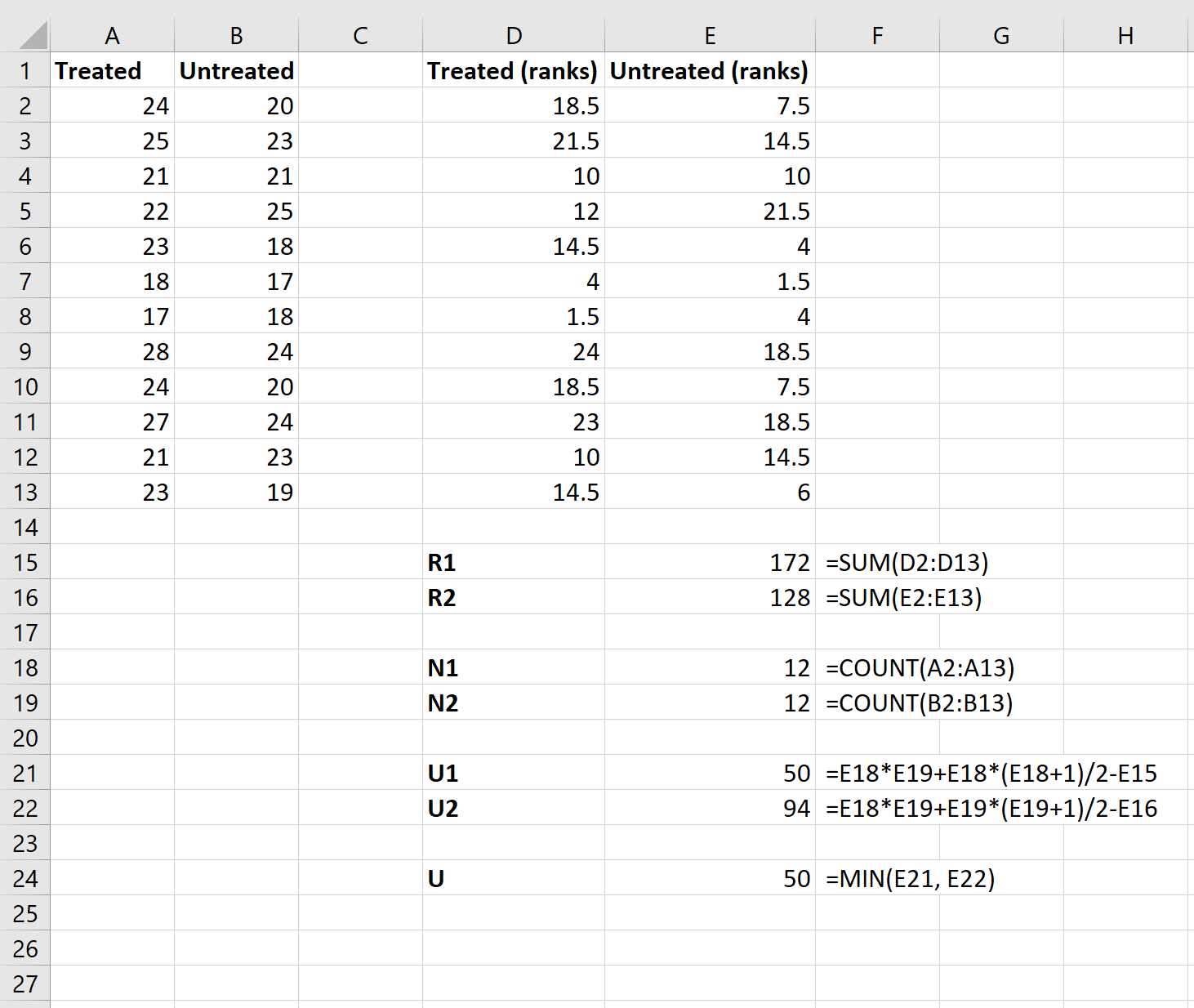
Passaggio 3: calcolare i valori necessari per la statistica del test.

Successivamente, utilizzeremo le seguenti formule per calcolare la somma dei ranghi per ciascun gruppo, la dimensione del campione per ciascun gruppo, la statistica U-test per ciascun gruppo e la statistica U-test complessiva:

Passaggio 4: calcolare la statistica z-test e il corrispondente valore p.

Infine, utilizzeremo le seguenti formule per calcolare la statistica z-test e il corrispondente valore p per determinare se dovremmo rifiutare o meno l’ipotesi nulla:

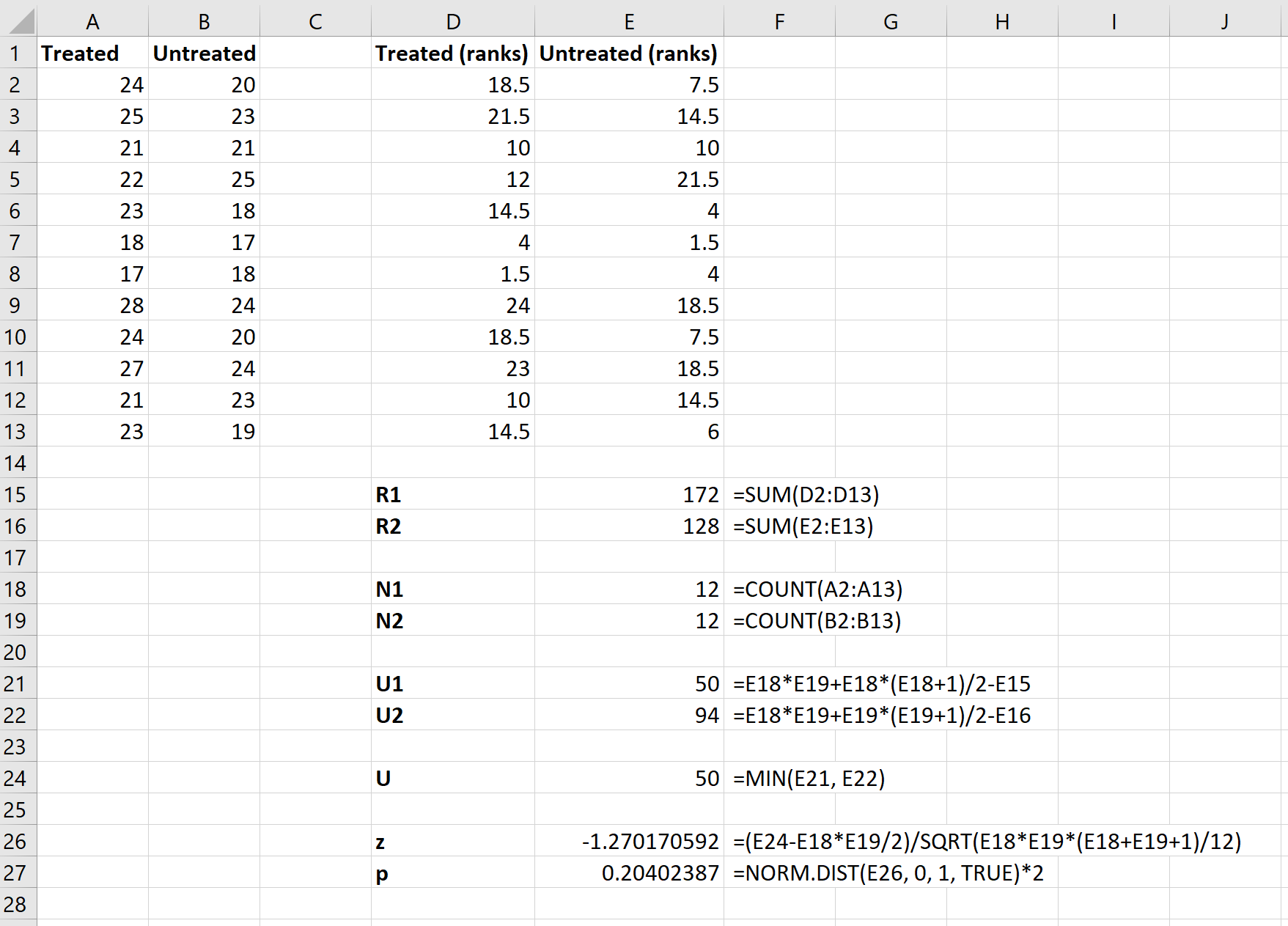
L’ipotesi nulla del test afferma che entrambi i gruppi hanno lo stesso mpg medio. Poiché il valore p del test ( 0,20402387 ) non è inferiore al nostro livello di significatività di 0,05, non riusciamo a rifiutare l’ipotesi nulla.

Non abbiamo prove sufficienti per affermare che il vero mpg medio sia diverso tra i due gruppi.