Come interpretare l'errore standard residuo

L’ errore standard residuo viene utilizzato per misurare la precisione con cui un modello di regressione si adatta a un set di dati.

In termini semplici, misura la deviazione standard dei residui in un modello di regressione.

Viene calcolato come segue:

Errore standard residuo = √ Σ(y – ŷ) ² /df

Oro:

• y: il valore osservato
• ŷ: il valore previsto
• df: i gradi di libertà, calcolati come numero totale di osservazioni – numero totale di parametri del modello.

Quanto più piccolo è l’errore standard residuo, tanto meglio il modello di regressione si adatta a un set di dati. Al contrario, maggiore è l’errore standard residuo, peggiore è l’adattamento del modello di regressione a un set di dati.

Un modello di regressione che ha un errore standard residuo piccolo avrà punti dati strettamente raggruppati attorno alla linea di regressione adattata:

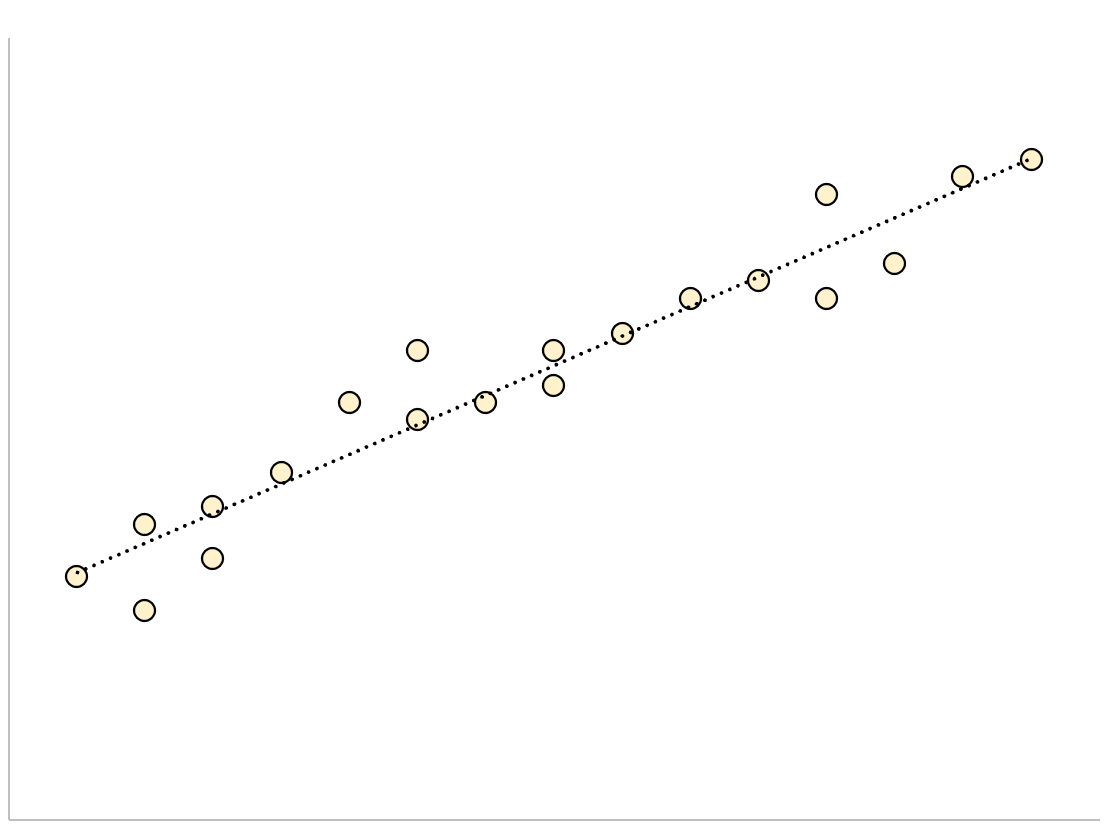
I residui di questo modello (la differenza tra i valori osservati e i valori previsti) saranno piccoli, il che significa che anche l’errore standard residuo sarà piccolo.

Al contrario, un modello di regressione che ha un errore standard residuo ampio avrà punti dati più vagamente sparsi attorno alla linea di regressione adattata:

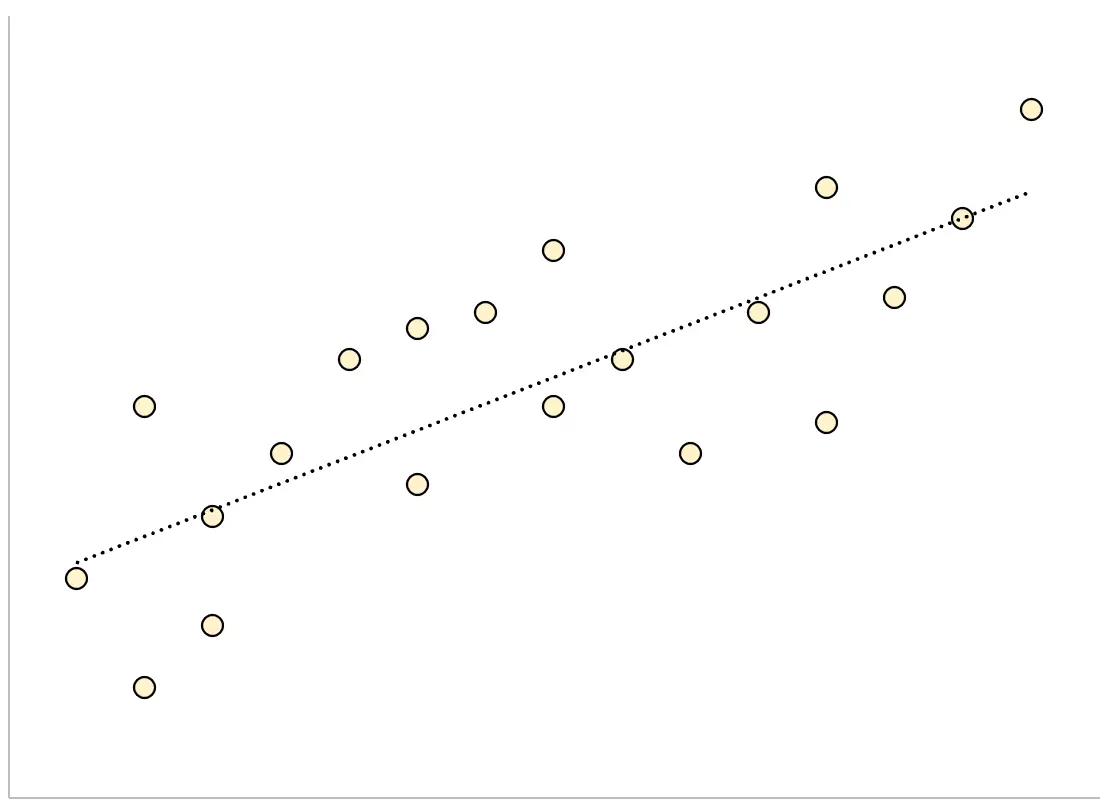
I residui di questo modello saranno maggiori, il che significa che anche l’errore standard residuo sarà maggiore.

L’esempio seguente mostra come calcolare e interpretare l’errore standard residuo di un modello di regressione in R.

Esempio: interpretazione dell’errore standard residuo

Supponiamo di voler adattare il seguente modello di regressione lineare multipla:

mpg = β ₀ + β ₁ (cilindrata) + β ₂ (potenza)

Questo modello utilizza le variabili predittive “cilindrata” e “potenza” per prevedere le miglia per gallone percorse da una determinata automobile.

Il codice seguente mostra come adattare questo modello di regressione in R:

 #load built-in mtcars dataset
data(mtcars)

#fit regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Call:
lm(formula = mpg ~ disp + hp, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-4.7945 -2.3036 -0.8246 1.8582 6.9363 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

Verso la fine del risultato, possiamo vedere che l’errore standard residuo di questo modello è 3,127 .

Questo ci dice che il modello di regressione prevede il mpg dell’auto con un errore medio di circa 3.127.

Utilizzo dell’errore standard residuo per confrontare i modelli

L’errore standard residuo è particolarmente utile per confrontare l’adattamento di diversi modelli di regressione.

Ad esempio, supponiamo di adattare due diversi modelli di regressione per prevedere il consumo di carburante dell’auto. L’errore standard residuo di ciascun modello è il seguente:

• Errore standard residuo del modello 1: 3,127
• Errore standard residuo del modello 2: 5,657

Poiché il Modello 1 ha un errore standard residuo inferiore, si adatta meglio ai dati rispetto al Modello 2. Pertanto, preferiremmo utilizzare il Modello 1 per prevedere il mpg dell’auto, perché le previsioni che fa sono più vicine ai valori mpg osservati delle auto.

Risorse addizionali

Come eseguire una regressione lineare semplice in R
Come eseguire la regressione lineare multipla in R
Come creare una trama residua in R