Come interpretare l'errore quadratico medio (rmse)

L’analisi di regressione è una tecnica che possiamo utilizzare per comprendere la relazione tra una o più variabili predittive e una variabile di risposta .

Un modo per valutare quanto bene un modello di regressione si adatta a un set di dati è calcolare l’ errore quadratico medio , che è una metrica che ci indica la distanza media tra i valori previsti del modello e i valori effettivi del set di dati.

Più basso è l’RMSE, migliore è la capacità di un dato modello di “adattarsi” a un set di dati.

La formula per trovare l’errore quadratico medio, spesso abbreviata RMSE , è:

RMSE = √ Σ(P _i – O _i ) ² / n

Oro:

• Σ è un simbolo di fantasia che significa “somma”
• _Pi è il valore previsto per l’ ^iesima osservazione nel set di dati
• O _i è il valore osservato per l’ ^iesima osservazione nel set di dati
• n è la dimensione del campione

L’esempio seguente mostra come interpretare l’RMSE per un determinato modello di regressione.

Esempio: come interpretare RMSE per un modello di regressione

Supponiamo di voler costruire un modello di regressione che utilizzi le “ore studiate” per prevedere il “voto dell’esame” degli studenti in un particolare esame di ammissione all’università.

Raccogliamo i seguenti dati per 15 studenti:

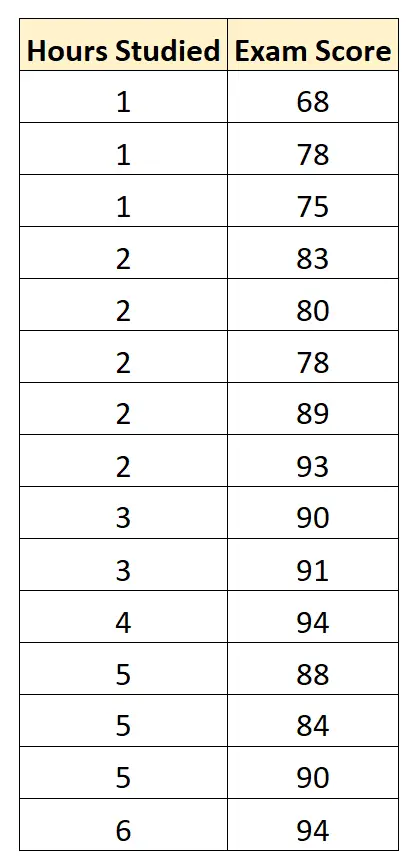
Utilizziamo quindi software statistici (come Excel, SPSS, R, Python), ecc. per trovare il seguente modello di regressione adattata:

Punteggio esame = 75,95 + 3,08* (ore studiate)

Possiamo quindi utilizzare questa equazione per prevedere il punteggio dell’esame di ogni studente, in base al numero di ore di studio:

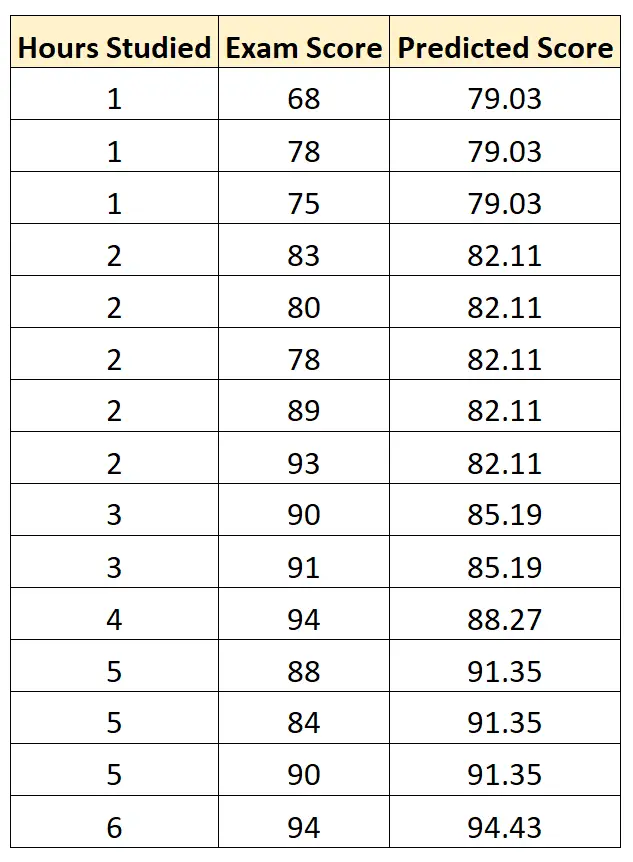
Possiamo quindi calcolare la differenza al quadrato tra ciascun punteggio dell’esame previsto e il punteggio effettivo dell’esame. Possiamo quindi fare la radice quadrata della media di queste differenze:

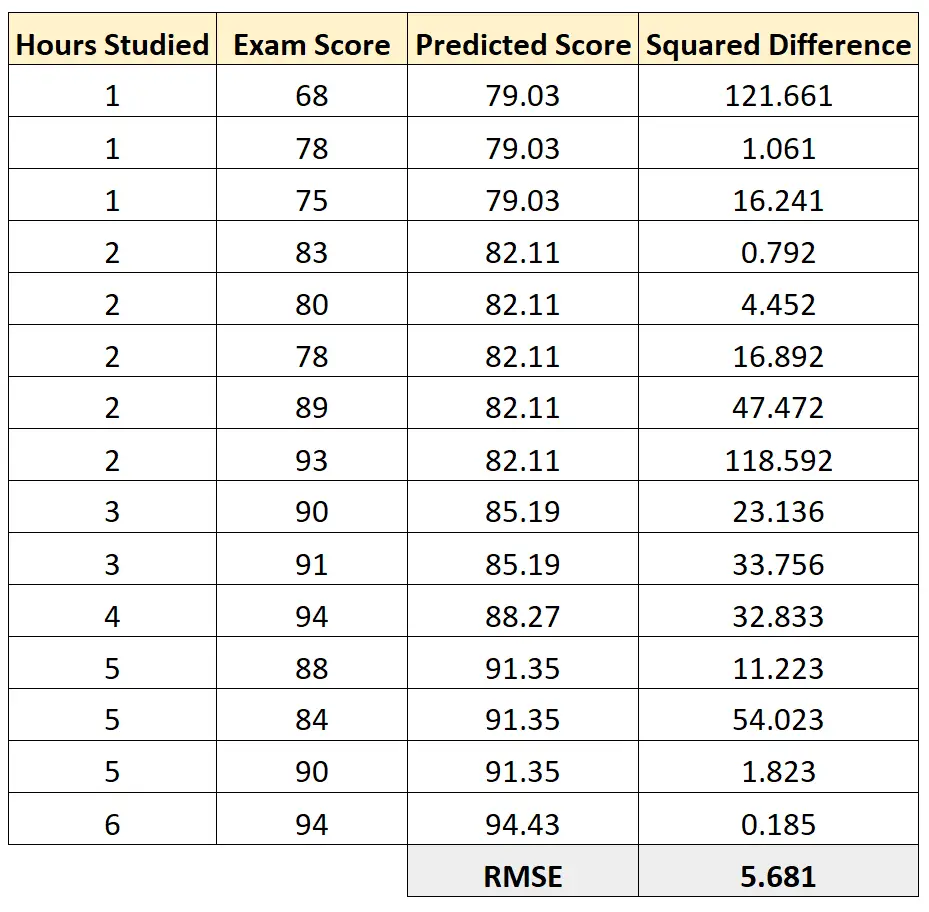
L’RMSE di questo modello di regressione risulta essere 5.681 .

Ricordiamo che i residui di un modello di regressione sono le differenze tra i valori dei dati osservati e i valori previsti del modello.

Residuo = (P _i – O _i )

Oro

• _Pi è il valore previsto per l’ ^iesima osservazione nel set di dati
• O _i è il valore osservato per l’ ^iesima osservazione nel set di dati

E ricorda che l’RMSE di un modello di regressione viene calcolato come segue:

RMSE = √ Σ(P _i – O _i ) ² / n

Ciò significa che l’RMSE rappresenta la radice quadrata della varianza dei residui.

Questo è un valore utile da conoscere perché ci dà un’idea della distanza media tra i valori dei dati osservati e i valori dei dati previsti.

Ciò contrasta con l’R quadrato del modello, che ci dice quanta parte della varianza nella variabile di risposta può essere spiegata dalle variabili predittive del modello.

Confronto dei valori RMSE di diversi modelli

L’RMSE è particolarmente utile per confrontare l’adattamento di diversi modelli di regressione.

Ad esempio, supponiamo di voler costruire un modello di regressione per prevedere i punteggi degli esami degli studenti e di voler trovare il miglior modello possibile tra diversi modelli potenziali.

Supponiamo di adattare tre diversi modelli di regressione e di trovare i corrispondenti valori RMSE:

• RMSE del modello 1: 14.5
• RMSE del modello 2: 16.7
• RMSE del modello 3: 9.8

Il modello 3 ha l’RMSE più basso, il che ci dice che è in grado di adattarsi al meglio al set di dati tra i tre potenziali modelli.

Risorse addizionali

Calcolatore RMSE
Come calcolare l’RMSE in Excel
Come calcolare l’RMSE in R
Come calcolare l’RMSE in Python