Come leggere una matrice di covarianza

La covarianza è una misura di come i cambiamenti in una variabile sono associati ai cambiamenti in una seconda variabile. Più specificamente, è una misura del grado in cui due variabili sono linearmente associate.

Una matrice di covarianza è una matrice quadrata che mostra la covarianza tra molte variabili diverse. Questo può essere un modo utile per comprendere come le diverse variabili sono correlate in un set di dati.

L’esempio seguente mostra come leggere in pratica una matrice di covarianza.

Come leggere una matrice di covarianza

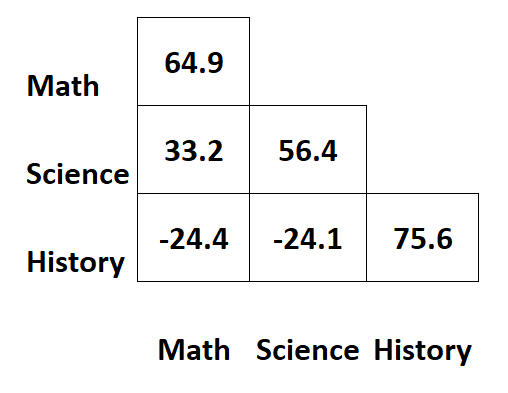
Supponiamo di avere la seguente matrice di covarianza che contiene informazioni sui punteggi degli esami per tre diverse materie per gli studenti:

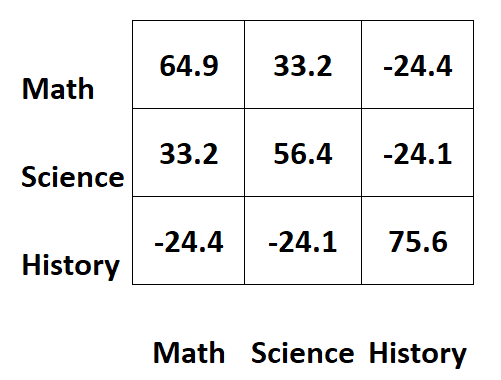
I valori lungo le diagonali della matrice rappresentano le varianze di ciascun soggetto.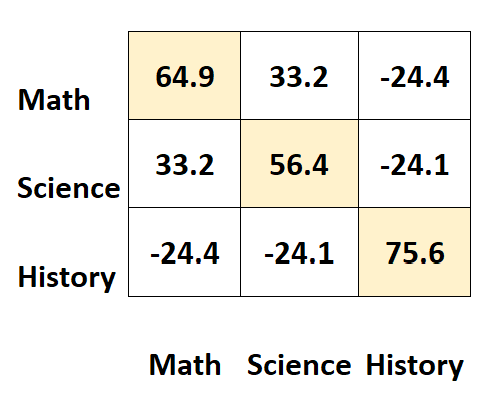

Per esempio:

• La varianza dei risultati di matematica è 64,9 .
• La varianza dei punteggi scientifici è 56,4 .
• La varianza dei punteggi storici è 75,6 .

Gli altri valori della matrice rappresentano le covarianze tra i diversi soggetti.

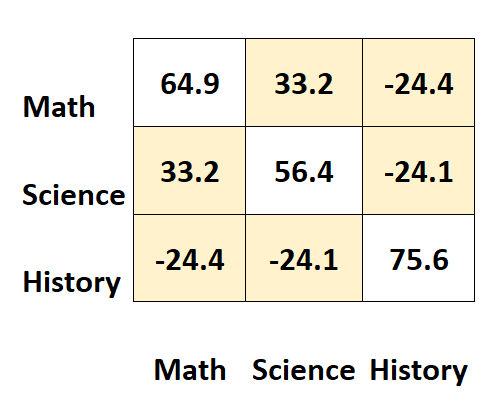
Per esempio:

• La covarianza tra i punteggi di matematica e scienze è 33,2 .
• La covarianza tra i punteggi in matematica e in storia è –24,4 .
• La covarianza tra i punteggi di scienza e storia è –24,1 .

Un numero positivo per la covarianza indica che due variabili tendono ad aumentare o diminuire in tandem.

Ad esempio, matematica e scienze hanno una covarianza positiva ( 33,2 ), indicando che gli studenti che ottengono punteggi elevati in matematica tendono ad ottenere punteggi elevati anche in scienze.

Al contrario, gli studenti che ottengono scarsi risultati in matematica tendono ad avere scarsi risultati anche in scienze.

Un numero negativo per la covarianza indica che all’aumentare di una variabile, una seconda variabile tende a diminuire.

Ad esempio, matematica e storia hanno una covarianza negativa ( -24,44 ), indicando che gli studenti che ottengono risultati elevati in matematica tendono ad avere risultati bassi in storia.

Al contrario, gli studenti che ottengono punteggi bassi in matematica tendono ad ottenere punteggi alti in storia.

Una nota sulla simmetria di una matrice di covarianza

Va notato che una matrice di covarianza è perfettamente simmetrica.

Ad esempio, la cella in alto a destra mostra esattamente lo stesso valore della cella in basso a sinistra:

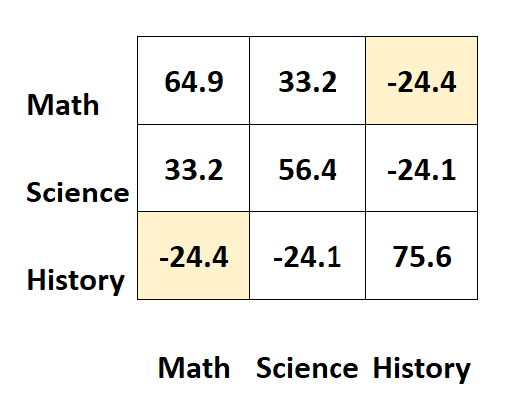
Infatti, le due celle misurano la covarianza tra storia e matematica.

Poiché una matrice di covarianza è simmetrica, metà dei valori di covarianza visualizzati nella matrice sono ridondanti e non necessari.

Pertanto, a volte verrà visualizzata solo metà della matrice di covarianza:

Quando utilizzare una matrice di covarianza

In pratica, spesso sarà necessario creare e interpretare una matrice di correlazione più spesso di una matrice di covarianza.

Tuttavia, le matrici di covarianza vengono spesso utilizzate “dietro le quinte” per diversi algoritmi e modelli di machine learning.

Ad esempio, la matrice di covarianza viene utilizzata durante l’analisi delle componenti principali , che ci aiuta a comprendere i modelli sottostanti in un set di dati contenente un gran numero di variabili.

Risorse addizionali

I seguenti tutorial spiegano come creare una matrice di covarianza utilizzando diversi software statistici:

Come creare una matrice di covarianza in R
Come creare una matrice di covarianza in Python
Come creare una matrice di covarianza in SPSS
Come creare una matrice di covarianza in Excel