Come leggere la tabella della distribuzione del chi quadrato

Questo tutorial spiega come leggere e interpretare il grafico della distribuzione del chi-quadrato.

Qual è la tabella di distribuzione del chi quadrato?

La tabella della distribuzione Chi-quadrato è una tabella che mostra i valori critici della distribuzione Chi-quadrato. Per utilizzare la tabella di distribuzione Chi-quadrato, è necessario conoscere solo due valori:

• Gradi di libertà per il test del Chi quadrato
• Il livello alfa del test (le scelte comuni sono 0,01, 0,05 e 0,10)

L’immagine seguente mostra le prime 20 righe della tabella di distribuzione Chi-quadrato, con i gradi di libertà sul lato sinistro della tabella e i livelli alfa nella parte superiore della tabella:

Nota: qui è possibile trovare una tabella completa della distribuzione del chi quadrato con più gradi di libertà.

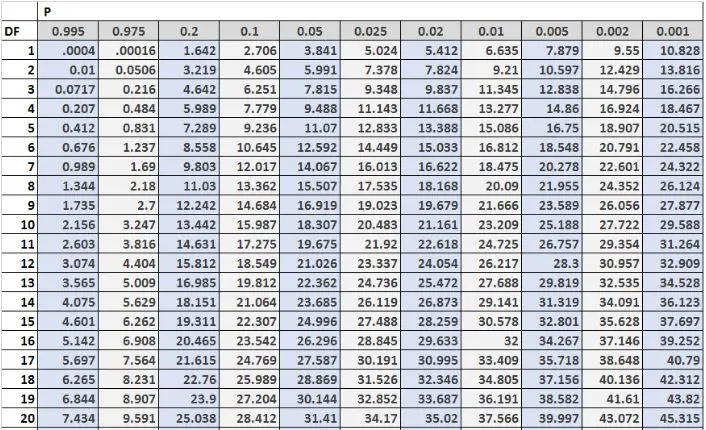
I valori critici nella tabella vengono spesso confrontati con le statistiche di test di un test Chi-quadrato. Se la statistica del test è maggiore del valore critico riportato nella tabella, è possibile rifiutare l’ipotesi nulla del test Chi quadrato e concludere che i risultati del test sono statisticamente significativi.

Esempi di utilizzo della tabella di distribuzione chi quadrato

Mostreremo come utilizzare la tabella di distribuzione Chi-quadrato con i seguenti tre tipi di test Chi-quadrato:

• Test chi quadrato per l’indipendenza
• Test chi quadrato per la bontà di adattamento
• Test del chi quadrato per l’omogeneità

Test chi quadrato per l’indipendenza

Usiamo un test Chi-quadrato per l’indipendenza quando vogliamo verificare se esiste o meno un’associazione significativa tra due variabili categoriali.

Esempio: supponiamo di voler sapere se il genere è associato o meno alla preferenza per un partito politico. Prendiamo un semplice campione casuale di 500 elettori e chiediamo loro quale sia la loro preferenza per il partito politico. Utilizzando un livello di significatività di 0,05, conduciamo un test chi-quadrato per determinare se il genere è associato alla preferenza del partito politico. La tabella seguente presenta i risultati dell’indagine:

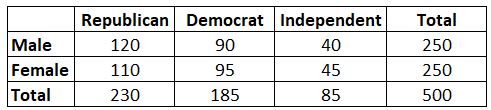
Risulta che la statistica del test per questo test del chi quadrato è 0,864.

Quindi possiamo trovare il valore critico del test nella tabella di distribuzione del Chi quadrato. I gradi di libertà sono uguali a (#righe-1) * (#colonne-1) = (2-1) * (3-1) = 2 e il problema ci ha detto che dovremmo usare un livello alfa di 0,05 Quindi, secondo la tabella di distribuzione del chi quadrato, il valore critico del test è 5.991 .

Poiché la nostra statistica test è inferiore al nostro valore critico, non riusciamo a rifiutare l’ipotesi nulla. Ciò significa che non abbiamo prove sufficienti per affermare che esista un’associazione tra le preferenze di genere e quelle dei partiti politici.

Test chi quadrato per la bontà di adattamento

Usiamo un test di bontà di adattamento del chi quadrato quando vogliamo verificare se una variabile categoriale segue o meno una distribuzione ipotetica.

Esempio: il proprietario di un negozio afferma che il 30% di tutti i suoi clienti del fine settimana vengono il venerdì, il 50% il sabato e il 20% la domenica. Un ricercatore indipendente visita il negozio in un fine settimana casuale e trova 91 clienti il venerdì, 104 il sabato e 65 la domenica. Utilizzando un livello di significatività pari a 0,10, eseguiamo un test chi quadrato per verificare la bontà dell’adattamento e determinare se i dati sono coerenti con l’affermazione del proprietario del negozio.

In questo caso, la statistica del test risulta essere 10.616.

Quindi possiamo trovare il valore critico del test nella tabella di distribuzione del Chi quadrato. I gradi di libertà sono uguali a (#outcomes-1) = 3-1 = 2 e il problema ci dice che dovremmo usare un livello alfa di 0,10. Quindi, secondo la tabella di distribuzione del Chi-quadrato, il valore critico del test è 4.605 .

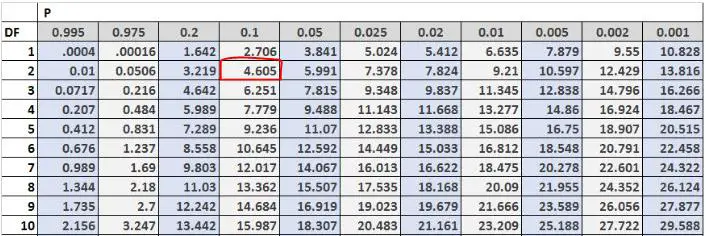
Poiché la nostra statistica test è maggiore del nostro valore critico, rifiutiamo l’ipotesi nulla. Ciò significa che abbiamo prove sufficienti per affermare che la reale distribuzione dei clienti che vengono in questo negozio nel fine settimana non è pari al 30% il venerdì, al 50% il sabato e al 20% la domenica.

Test del chi quadrato per l’omogeneità

Utilizziamo un test Chi-quadrato per l’omogeneità quando vogliamo verificare formalmente se esiste o meno una differenza nelle proporzioni tra più gruppi.

Esempio: un centro di allenamento di basket vuole vedere se due nuovi programmi di allenamento migliorano la percentuale dei suoi giocatori che superano una prova di tiro difficile. 172 giocatori vengono assegnati in modo casuale al programma 1, 173 al programma 2 e 215 al programma corrente. Dopo aver utilizzato i programmi di allenamento per un mese, i giocatori sostengono un test di tiro. La tabella seguente mostra il numero di giocatori che superano la prova di tiro, in base al programma utilizzato.

Utilizzando un livello di significatività pari a 0,05, eseguiamo un test chi quadrato per determinare se il tasso di successo è lo stesso per ciascun programma di formazione.

Risulta che la statistica del test per questo test del Chi-quadrato è 4.208.

Quindi possiamo trovare il valore critico del test nella tabella di distribuzione del Chi quadrato. I gradi di libertà sono uguali a (#righe-1) * (#colonne-1) = (2-1) * (3-1) = 2 e il problema ci ha detto che dovremmo usare un livello alfa di 0,05 Quindi, secondo la tabella di distribuzione del chi quadrato, il valore critico del test è 5.991 .

Poiché la nostra statistica test è inferiore al nostro valore critico, non riusciamo a rifiutare l’ipotesi nulla. Ciò significa che non abbiamo prove sufficienti per affermare che i tre programmi di formazione producono risultati diversi.