Come leggere la tabella della distribuzione binomiale

La tabella di distribuzione binomiale   è una tabella che mostra le probabilità associate alla distribuzione binomiale . Per utilizzare la tabella di distribuzione binomiale, sono necessari solo tre valori:

• n: il numero di tentativi
• r: il numero di “successi” durante n tentativi
• p: la probabilità di successo di una determinata prova

Utilizzando questi tre numeri, puoi utilizzare la tabella di distribuzione binomiale per trovare la probabilità di ottenere esattamente r successi nel corso di n prove quando la probabilità di successo in ciascuna prova è p .

I seguenti esempi illustrano come leggere la tabella della distribuzione binomiale.

Esempio 1

Domanda: Jessica effettua il 60% dei suoi tiri liberi. Se effettua 6 tiri liberi, qual è la probabilità che ne effettui esattamente 4?

Per rispondere a questa domanda, possiamo trovare il valore nella tabella di distribuzione binomiale che corrisponde a n = 6, r = 4 e p = 0,60:

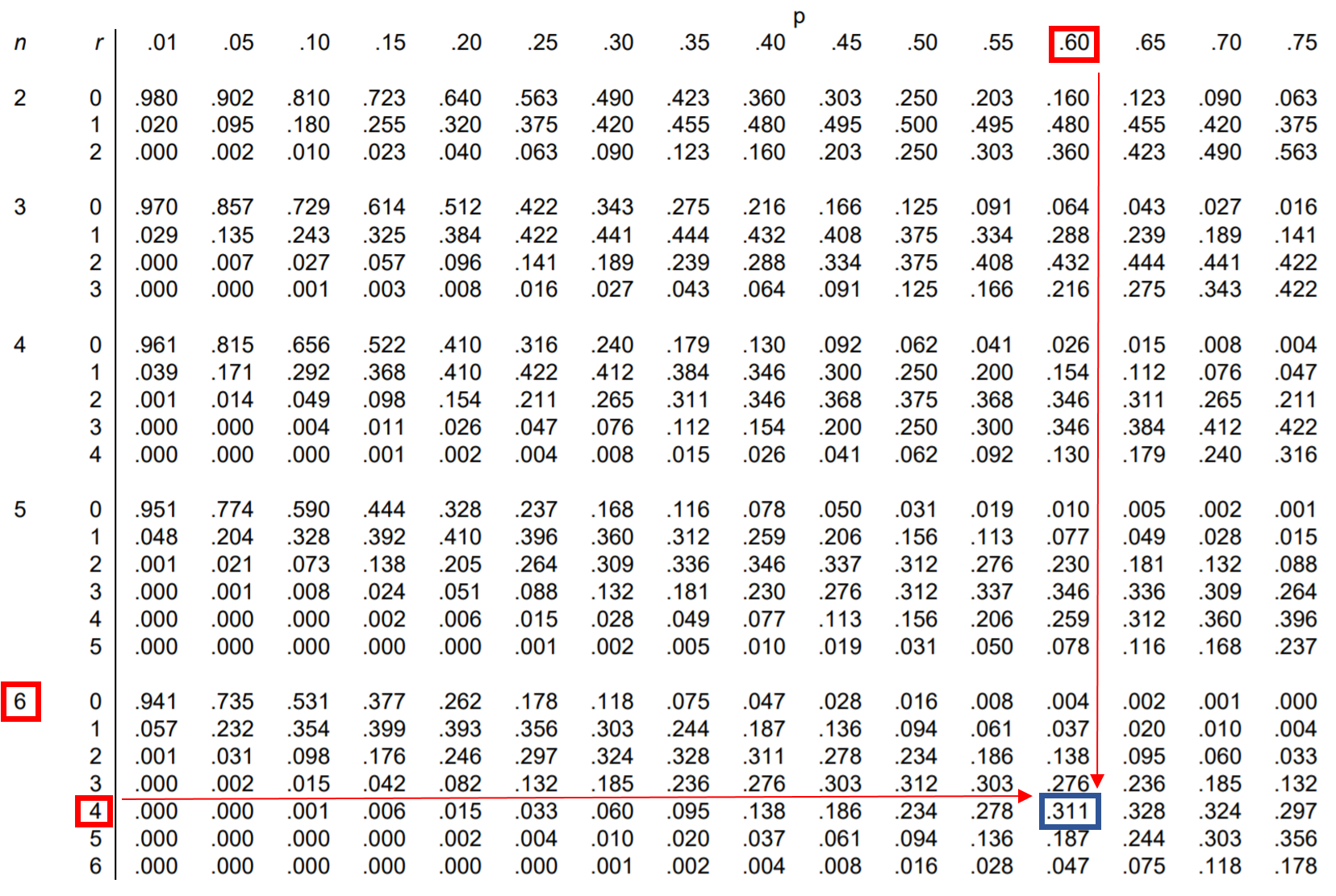
La probabilità che Jessica effettui esattamente 4 tiri liberi su 6 è 0,311 .

Esempio 2

Domanda: Jessica effettua il 60% dei suoi tiri liberi. Se effettua 6 tiri liberi, qual è la probabilità che ne effettui meno di 4?

Per trovare questa probabilità, devi effettivamente aggiungere le seguenti probabilità:

P(fa meno di 4) = P(fa 0) + P(fa 1) + P(fa 2) + P(fa 3)

Quindi, possiamo cercare ciascuna di queste quattro probabilità nella tabella della distribuzione binomiale e sommarle insieme:

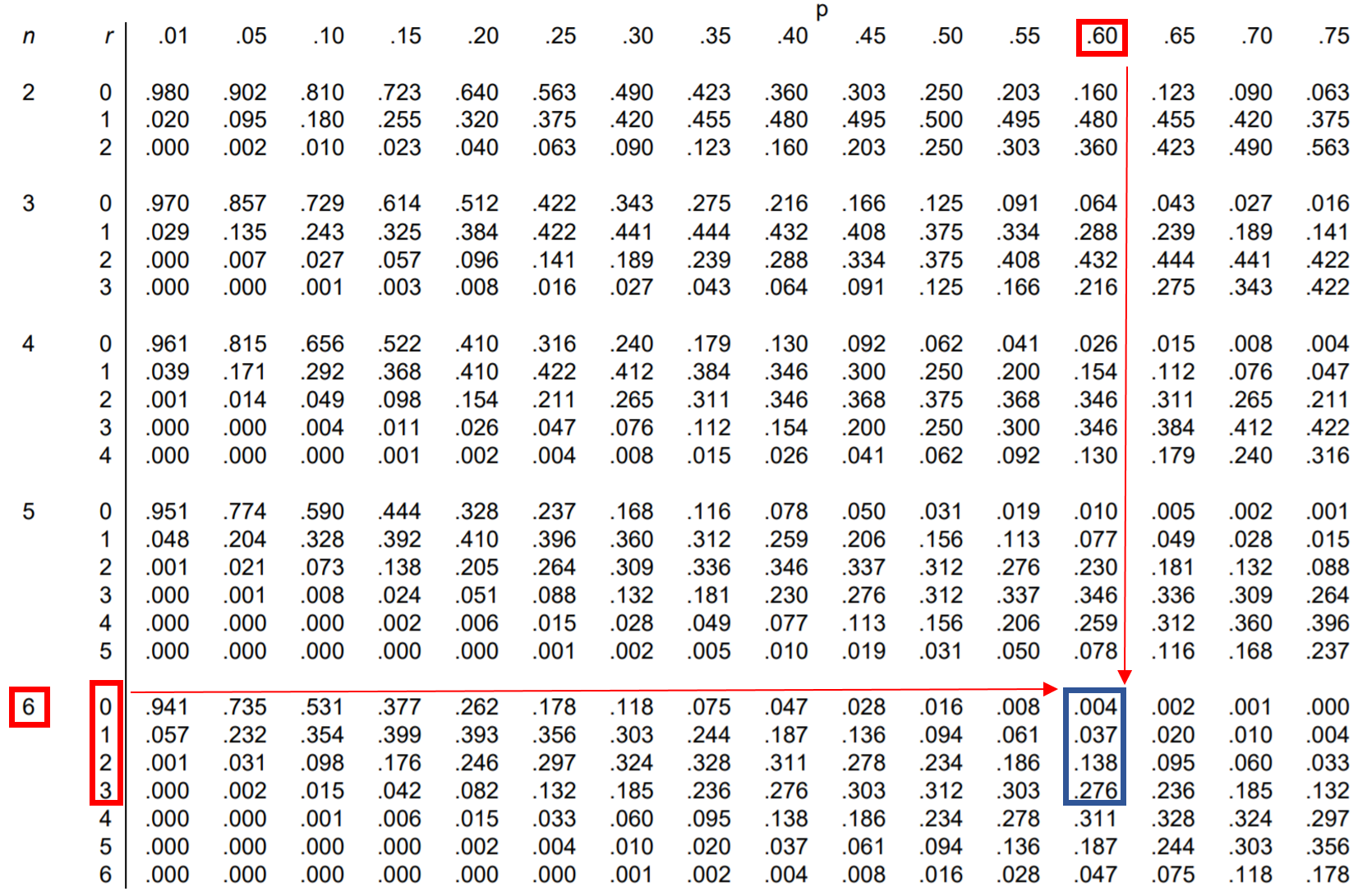
Dalla tabella, P(è inferiore a 4) = 0,004 + 0,037 + 0,138 + 0,276 = 0,455 .

La probabilità che Jessica effettui meno di 4 tiri liberi è 0,455 .

Esempio 3

Domanda: Jessica effettua il 60% dei suoi tiri liberi. Se effettua 6 tiri liberi, qual è la probabilità che ne effettui 4 o più?

Per trovare questa probabilità, dobbiamo aggiungere le seguenti probabilità:

P(fa 4 o più) = P(fa 4) + P(fa 5) + P(fa 6)

Quindi, possiamo cercare ciascuna di queste tre probabilità nella tabella della distribuzione binomiale e sommarle insieme:

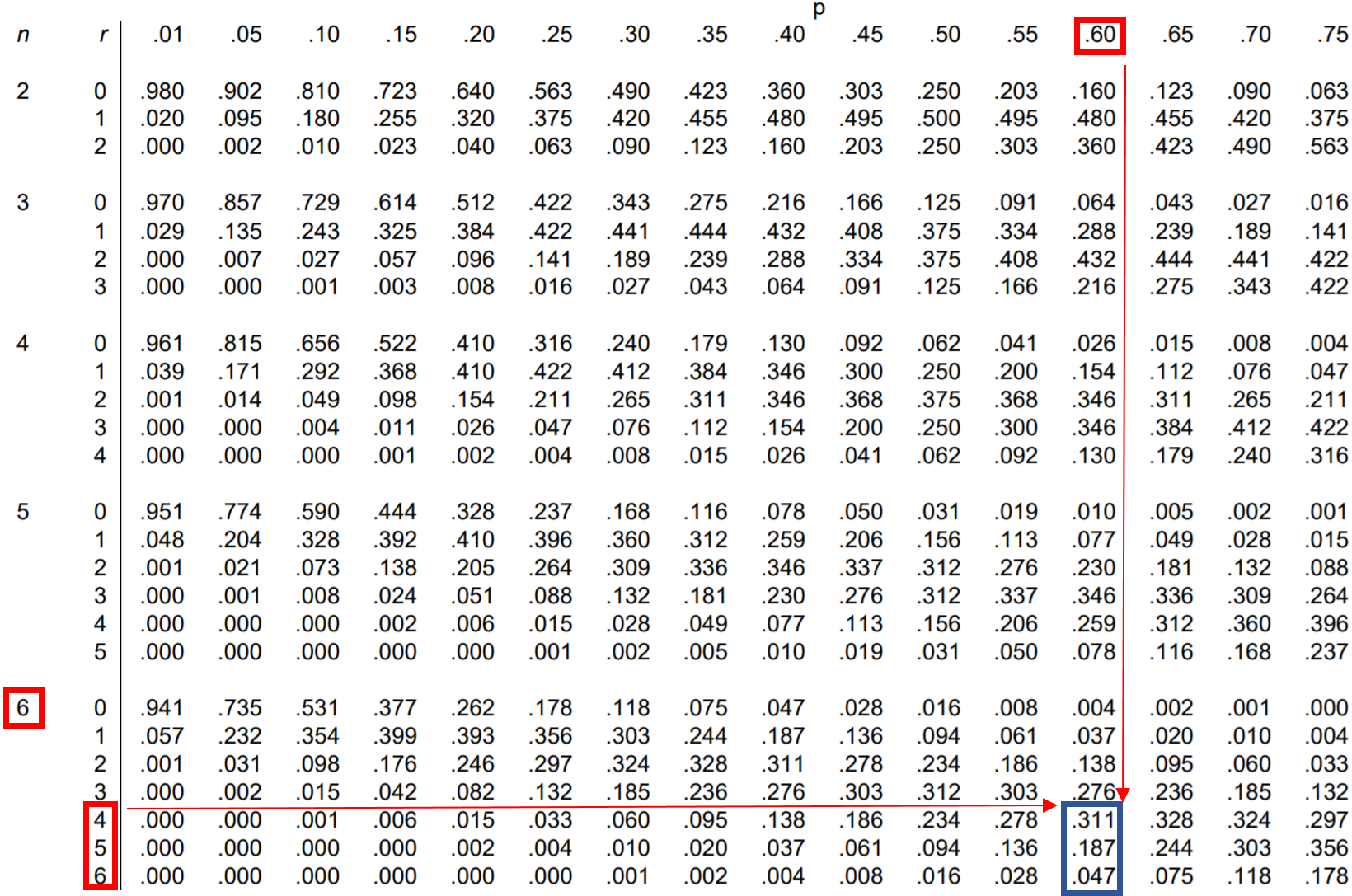
Dalla tabella, P(fa 4 o più) = 0,311 + 0,187 + 0,047 = 0,545 .

La probabilità che Jessica effettui 4 o più tiri liberi è 0,545 .