Come leggere una matrice di correlazione

Nelle statistiche, spesso cerchiamo di comprendere la relazione tra due variabili.

Ad esempio, potremmo voler comprendere la relazione tra il numero di ore di studio di uno studente e il voto ricevuto all’esame.

Un modo per quantificare questa relazione è utilizzare il coefficiente di correlazione di Pearson , che è una misura dell’associazione lineare tra due variabili . Ha un valore compreso tra -1 e 1 dove:

• -1 indica una correlazione lineare perfettamente negativa tra due variabili
• 0 indica alcuna correlazione lineare tra due variabili
• 1 indica una correlazione lineare perfettamente positiva tra due variabili

Quanto più il coefficiente di correlazione si allontana da zero, tanto più forte è la relazione tra le due variabili.

Correlati: cos’è considerata una correlazione “forte”?

Ma in alcuni casi, vogliamo comprendere la correlazione tra più coppie di variabili. In questi casi possiamo creare una matrice di correlazione , ovvero una tabella quadrata che mostra i coefficienti di correlazione tra diverse variabili.

Esempio di matrice di correlazione

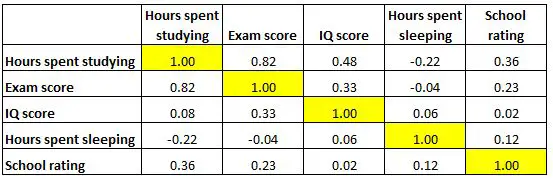
La matrice di correlazione seguente presenta i coefficienti di correlazione tra diverse variabili relative all’istruzione:

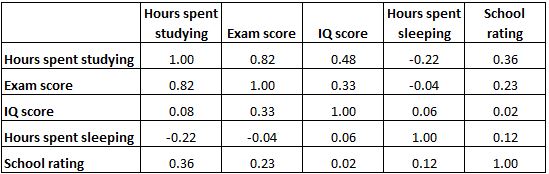
Ogni cella della tabella mostra la correlazione tra due variabili specifiche. Ad esempio, la cella evidenziata qui sotto mostra che la correlazione tra “ore trascorse a studiare” e “voto dell’esame” è 0,82 , indicando che sono fortemente correlati positivamente. Più ore trascorse a studiare sono strettamente legate a punteggi più alti negli esami.

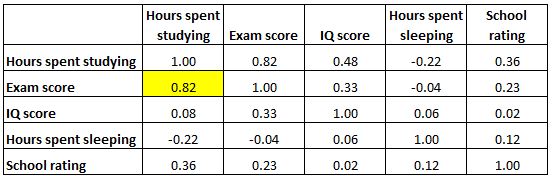
E la cella evidenziata di seguito mostra che la correlazione tra “ore trascorse a studiare” e “ore trascorse a dormire” è -0,22 , indicando che sono debolmente correlate negativamente. Più ore trascorse a studiare sono associate a meno ore trascorse a dormire.

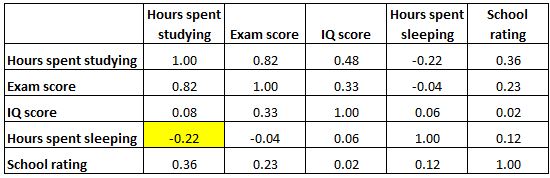
E la cella evidenziata di seguito mostra che la correlazione tra “ore trascorse a dormire” e “punteggio QI” è 0,06 , indicando che sono sostanzialmente non correlati. C’è pochissima associazione tra il numero di ore di sonno di uno studente e il suo punteggio QI.

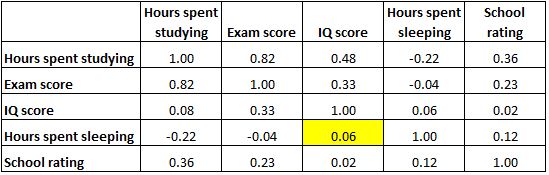
Si noti inoltre che i coefficienti di correlazione lungo la diagonale della tabella sono tutti pari a 1 perché ogni variabile è perfettamente correlata con se stessa. Queste celle non sono utili per l’interpretazione.

Variazioni della matrice di correlazione

Si noti che una matrice di correlazione è perfettamente simmetrica. Ad esempio, la cella in alto a destra mostra esattamente lo stesso valore della cella in basso a sinistra:

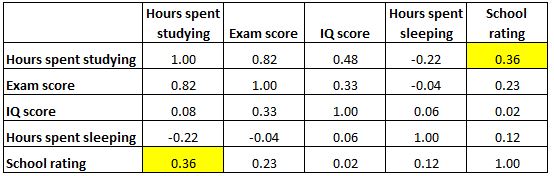
Le due celle, infatti, misurano la correlazione tra “ore trascorse a studiare” e “voto scolastico”.

Poiché una matrice di correlazione è simmetrica, metà dei coefficienti di correlazione visualizzati nella matrice sono ridondanti e non necessari. Pertanto, a volte verrà visualizzata solo metà della matrice di correlazione:

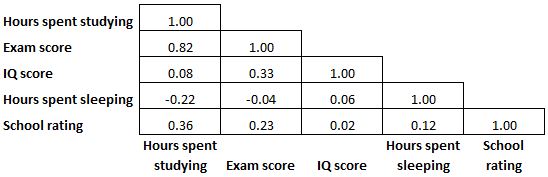
E a volte una matrice di correlazione sarà colorata come una mappa termica per rendere i coefficienti di correlazione ancora più facili da leggere:

Quando utilizzare una matrice di correlazione

In pratica, una matrice di correlazione viene comunemente utilizzata per tre motivi:

1. Una matrice di correlazione riassume opportunamente un insieme di dati.

Una matrice di correlazione è un modo semplice per riassumere le correlazioni tra tutte le variabili in un set di dati. Ad esempio, supponiamo di avere il seguente set di dati contenente le seguenti informazioni per 1.000 studenti:

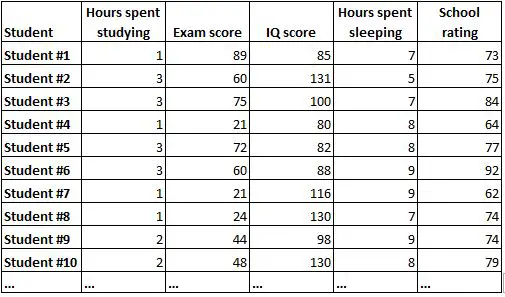
Sarebbe molto difficile comprendere la relazione tra ciascuna variabile semplicemente osservando i dati grezzi. Fortunatamente, una matrice di correlazione può aiutarci a comprendere rapidamente le correlazioni tra ciascuna coppia di variabili.

2. Una matrice di correlazione funge da diagnosi per la regressione.

Uno dei presupposti chiave della regressione lineare multipla è che nessuna variabile indipendente nel modello è fortemente correlata con qualsiasi altra variabile nel modello.

Quando due variabili indipendenti sono altamente correlate, si verifica un problema chiamato multicollinearità e può rendere difficile l’interpretazione dei risultati della regressione.

Uno dei modi più semplici per individuare un potenziale problema di multicollinearità è osservare una matrice di correlazione e verificare visivamente se qualcuna delle variabili è altamente correlata tra loro.

3. Una matrice di correlazione può essere utilizzata come input per altre analisi.

Una matrice di correlazione viene utilizzata come input per altre analisi complesse come l’analisi fattoriale esplorativa e i modelli di equazioni strutturali.

Risorse addizionali

I seguenti tutorial spiegano come creare una matrice di correlazione utilizzando vari software statistici:

Come creare una matrice di correlazione in Excel
Come creare una matrice di correlazione in SPSS
Come creare una matrice di correlazione in Stata
Come creare una matrice di correlazione in Python