Come utilizzare la tabella z (con esempi)

Una tabella z è una tabella che indica quale percentuale di valori cade al di sotto di un determinato punteggio z in una distribuzione normale standard.

Un punteggio z ti dice semplicemente di quante deviazioni standard un singolo valore di dati cade dalla media. Viene calcolato come segue:

Punteggio z = (x – μ) / σ

Oro:

• x: valore del dato individuale
• μ: media della popolazione
• σ: deviazione standard della popolazione

Questo tutorial mostra diversi esempi di utilizzo della tabella z.

Esempio 1

I punteggi di un determinato esame di ammissione all’università sono normalmente distribuiti con media μ = 82 e deviazione standard σ = 8. Approssimativamente quale percentuale di studenti ottiene un punteggio inferiore a 84 all’esame?

Passaggio 1: trova il punteggio z.

Innanzitutto, troveremo lo z-score associato a un punteggio dell’esame pari a 84:

Punteggio z = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25

Passaggio 2: utilizza il grafico z per trovare la percentuale che corrisponde al punteggio z.

Successivamente, cercheremo il valore 0,25 nella tabella z:

Circa il 59,87% degli studenti ottiene un punteggio inferiore a 84 in questo esame.

Esempio 2

L’altezza delle piante in un certo giardino è normalmente distribuita con una media di μ = 26,5 pollici e una deviazione standard di σ = 2,5 pollici. Qual è approssimativamente la percentuale di piante alte più di 26 pollici?

Passaggio 1: trova il punteggio z.

Per prima cosa troveremo il punteggio z associato ad un’altezza di 26 pollici.

Punteggio z = (x – μ) / σ = (26 – 26,5) / 2,5 = -0,5 / 2,5 = -0,2

Passaggio 2: utilizza il grafico z per trovare la percentuale che corrisponde al punteggio z.

Successivamente cercheremo il valore -0.2   nella tabella z:

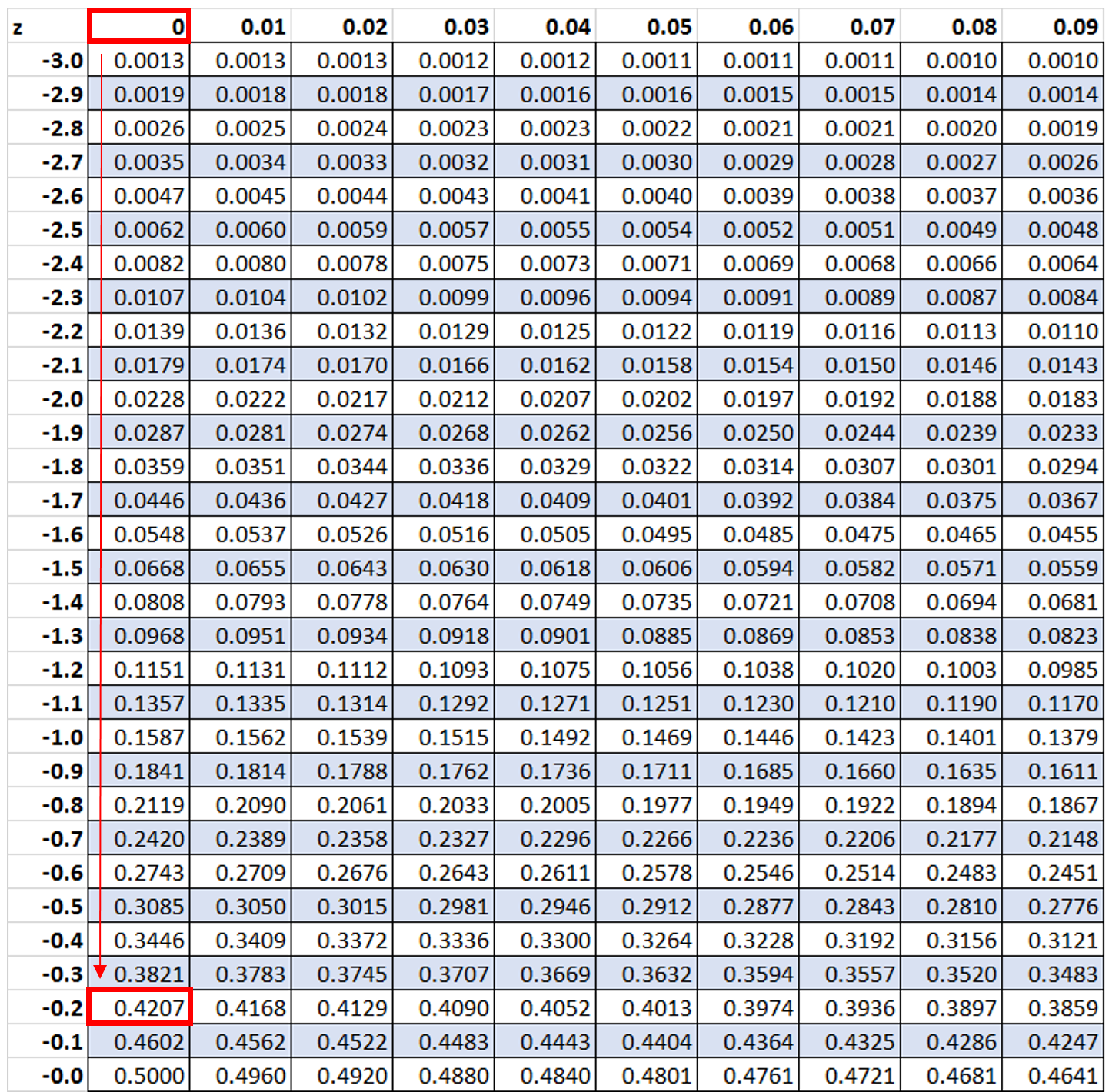
Vediamo che il 42,07% dei valori è inferiore allo z-score di -0,2. Tuttavia, in questo esempio vogliamo sapere quale percentuale di valori è maggiore di -0,2, che possiamo trovare utilizzando la formula 100% – 42,07% = 57,93%.

Quindi, circa il 59,87% delle piante in questo giardino sono alte più di 26 pollici.

Esempio 3

Il peso di una certa specie di delfini è distribuito normalmente con una media di μ = 400 libbre e una deviazione standard di σ = 25 libbre. Approssimativamente quale percentuale di delfini pesa tra 410 e 425 libbre?

Passaggio 1: trova i punteggi z.

Per prima cosa troveremo i punteggi z associati a 410 libri e 425 libri

Punteggio z di 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4

punteggio z di 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

Passaggio 2: utilizza il grafico z per trovare le percentuali che corrispondono a ciascun punteggio z.

Per prima cosa cercheremo il valore 0.4   nella tabella z:

Successivamente cercheremo il valore 1   nella tabella z:

Infine, sottraiamo il valore più piccolo dal valore più grande: 0,8413 – 0,6554 = 0,1859 .

Quindi, circa il 18,59% dei delfini pesa tra 410 e 425 libbre.

Risorse addizionali

Un’introduzione alla distribuzione normale
Calcolatore dell’area di distribuzione normale
Calcolatore del punteggio Z