Qual è il compromesso tra bias e varianza nel machine learning?

Per valutare le prestazioni di un modello su un set di dati, dobbiamo misurare quanto bene le previsioni del modello corrispondono ai dati osservati.

Per i modelli di regressione , la metrica più comunemente utilizzata è l’errore quadratico medio (MSE), calcolato come segue:

MSE = (1/n)*Σ(y _i – f(x _i )) ²

Oro:

• n: numero totale di osservazioni
• y _i : il valore di risposta dell’i ^-esima osservazione
• f( _xi ): Il valore di risposta previsto dell’i- ^esima osservazione

Più le previsioni del modello si avvicinano alle osservazioni, più basso sarà il MSE.

Tuttavia, ci preoccupiamo solo del test MSE : l’MSE quando il nostro modello viene applicato a dati invisibili. Questo perché ci interessa solo come funzionerà il modello su dati sconosciuti, non su dati esistenti.

Ad esempio, va bene se un modello che prevede i prezzi delle azioni ha un MSE basso sui dati storici, ma vogliamo davvero essere in grado di utilizzare il modello per prevedere con precisione i dati futuri.

Risulta che il test MSE può ancora essere suddiviso in due parti:

(1) Varianza: si riferisce all’importo che la nostra funzione f cambierebbe se la stimassimo utilizzando un set di addestramento diverso.

(2) Bias: si riferisce all’errore introdotto affrontando un problema reale, che può essere estremamente complicato, con un modello molto più semplice.

Scritto in termini matematici:

Test MSE = Var( f̂( x ₀ )) + [Bias( f̂( x ₀ ))] ² + Var(ε)

Test MSE = Varianza + Bias ² + Errore irriducibile

Il terzo termine, l’errore irriducibile, è l’errore che non può essere ridotto da nessun modello semplicemente perché c’è sempre rumore nella relazione tra l’insieme delle variabili esplicative e la variabile di risposta .

I modelli che hanno una distorsione elevata tendono ad avere una varianza bassa . Ad esempio, i modelli di regressione lineare tendono ad avere una distorsione elevata (assumendo una semplice relazione lineare tra le variabili esplicative e la variabile di risposta) e una varianza bassa (le stime del modello non cambieranno molto da campione a campione). l’altro).

Tuttavia, i modelli con bias basso tendono ad avere una varianza elevata . Ad esempio, i modelli non lineari complessi tendono ad avere una distorsione bassa (non assumere una certa relazione tra le variabili esplicative e la variabile di risposta) con una varianza elevata (le stime del modello possono cambiare significativamente da un campione di apprendimento a un altro).

Il compromesso bias-varianza

Il compromesso bias-varianza si riferisce al compromesso che avviene quando scegliamo di ridurre la distorsione, che generalmente aumenta la varianza, o di ridurre la varianza, che generalmente aumenta la distorsione.

Il grafico seguente offre un modo per visualizzare questo compromesso:

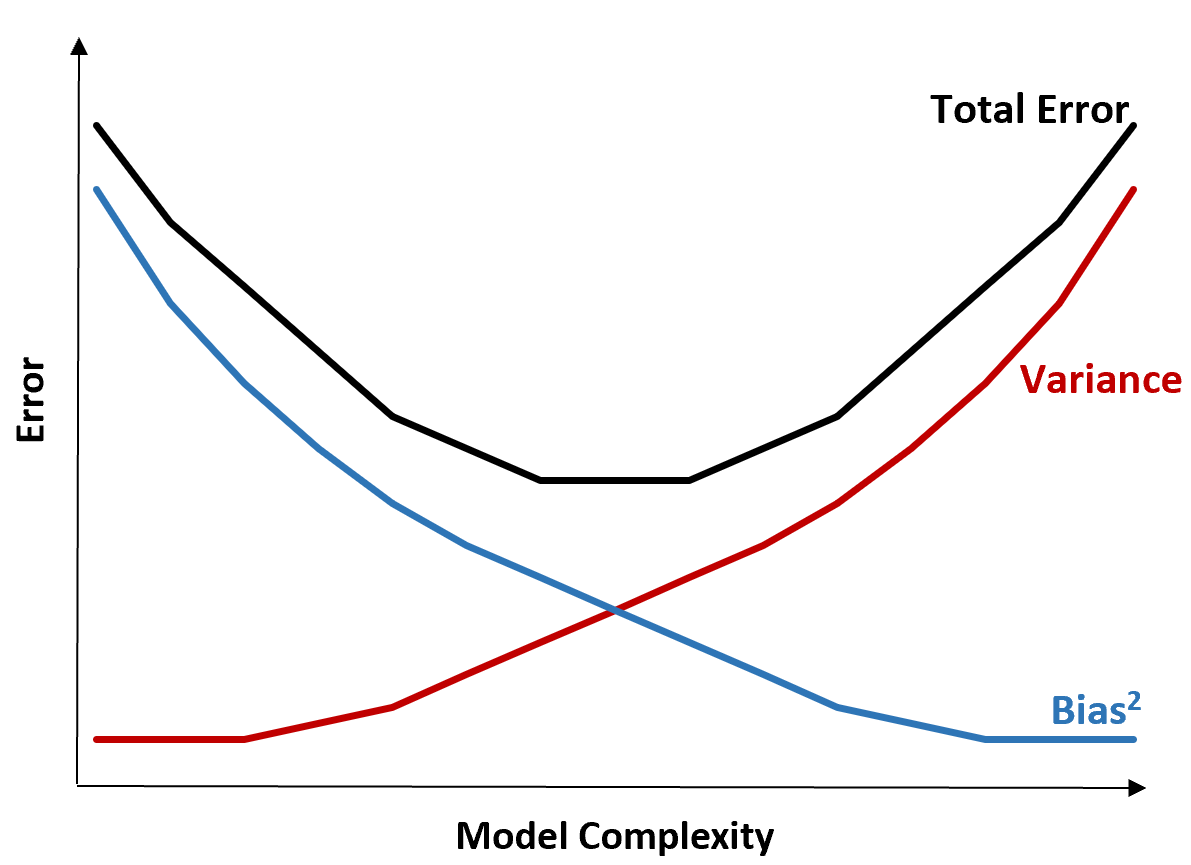
L’errore totale diminuisce all’aumentare della complessità del modello, ma solo fino a un certo punto. Oltre un certo punto, la varianza inizia ad aumentare e anche l’errore totale inizia ad aumentare.

In pratica, ci preoccupiamo solo di minimizzare l’errore totale di un modello, non necessariamente di minimizzare la varianza o la distorsione. Si scopre che il modo per ridurre al minimo l’errore totale è trovare il giusto equilibrio tra varianza e distorsione.

In altre parole, vogliamo un modello abbastanza complesso da catturare la vera relazione tra le variabili esplicative e la variabile di risposta, ma non troppo complesso da individuare modelli che in realtà non esistono.

Quando un modello è troppo complesso, si adatta eccessivamente ai dati. Ciò accade perché è troppo difficile trovare modelli nei dati di addestramento che siano semplicemente causati dal caso. È probabile che questo tipo di modello abbia prestazioni scarse su dati invisibili.

Ma quando un modello è troppo semplice, sottostima i dati. Ciò accade perché si presuppone che la vera relazione tra le variabili esplicative e la variabile di risposta sia più semplice di quanto non sia in realtà.

Il modo per selezionare modelli ottimali nell’apprendimento automatico è trovare un equilibrio tra bias e varianza per ridurre al minimo l’errore di testare il modello su dati futuri invisibili.

In pratica, il modo più comune per ridurre al minimo l’MSE dei test è utilizzare la convalida incrociata .