Come confrontare i box plot: con esempi

Un box plot è un tipo di grafico che visualizza il riepilogo di cinque cifre di un set di dati, che include:

• Il valore minimo
• Il primo quartile (il 25° percentile)
• Il valore mediano
• Il terzo quartile (il 75° percentile)
• Il valore massimo

Per realizzare un box plot, disegniamo un riquadro dal primo al terzo quartile. Successivamente, tracciamo una linea verticale in corrispondenza della mediana. Infine disegniamo i “baffi” dei quartili fino al valore minimo e massimo.

I boxplot sono utili perché ci consentono di comprendere rapidamente la distribuzione dei valori in un set di dati. Sono utili anche per confrontare due diversi set di dati.

Quando confrontiamo due o più boxplot, possiamo rispondere a quattro domande diverse:

1. Come si confrontano i valori mediani? Possiamo confrontare la linea verticale in ciascuna casella per determinare quale set di dati ha un valore mediano più alto.

2. Come si confronta la dispersione? Possiamo confrontare la lunghezza di ciascuna casella (che rappresenta la distanza tra Q1 e Q3 – l’intervallo interquartile) per determinare quale set di dati è più grande.

3. Come si confronta l’asimmetria? Più la linea verticale è vicina al primo trimestre, più il set di dati è distorto positivamente. Quanto più la linea verticale è vicina al terzo trimestre, tanto più distorta è la serie di dati.

4. Sono presenti valori anomali? Nei grafici a scatola, i valori anomali sono solitamente rappresentati da piccoli cerchi che si estendono oltre ciascun baffo. Un’osservazione è definita outlier se soddisfa uno dei seguenti criteri:

• Un’osservazione è inferiore a Q1 – 1,5*IQR
• Un’osservazione è maggiore di Q3 + 1,5*IQR

L’esempio seguente mostra come confrontare due diversi boxplot e rispondere a queste quattro domande.

Esempio: confronto tra box plot

I seguenti set di dati mostrano i risultati degli studenti che hanno utilizzato una delle due tecniche di studio per prepararsi all’esame:

Metodo 1: 78, 78, 79, 80, 80, 82, 82, 83, 83, 86, 86, 86, 86, 87, 87, 87, 88, 88, 88, 91

Metodo 2: 66, 66, 66, 67, 68, 70, 72, 75, 75, 78, 82, 83, 86, 88, 89, 90, 93, 94, 95, 98

Se creiamo boxplot per ciascun set di dati, ecco come apparirebbero:

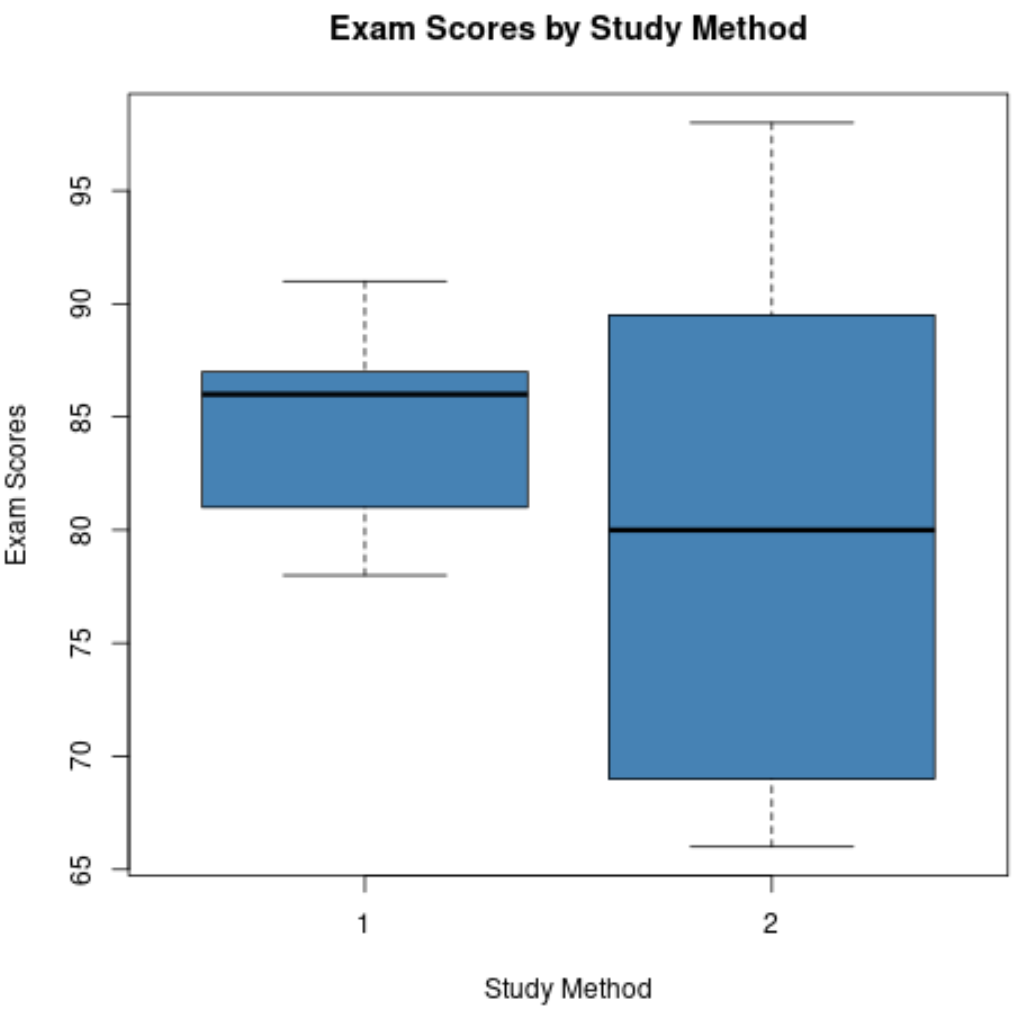
Possiamo confrontare questi due boxplot e rispondere alle seguenti quattro domande:

1. Come si confrontano i valori mediani? La linea al centro del box plot per il metodo di studio 1 è più alta della linea per il metodo di studio 2, indicando che gli studenti che hanno utilizzato il metodo di studio 1 hanno ottenuto un voto medio all’esame superiore.

2. Come si confronta la dispersione? Il box plot per il Metodo di studio 2 è molto più lungo di quello per il Metodo di studio 1, indicando che i punteggi degli esami sono molto più distribuiti tra gli studenti che hanno utilizzato il Metodo di studio 2.

3. Come si confronta l’asimmetria? La linea al centro del box plot per il metodo di studio 1 è vicina a Q3, indicando che la distribuzione dei punteggi degli esami per gli studenti che hanno utilizzato il metodo di studio 1 è distorta negativamente. Al contrario, la linea al centro del box plot per il metodo di studio 2 è vicina al centro del box, il che significa che la distribuzione dei punteggi è minimamente distorta.

4. Sono presenti valori anomali? Nessuno dei due boxplot presenta piccoli cerchi che si estendono oltre i baffi superiori o inferiori, il che significa che nessuno dei due set di dati presenta valori anomali chiari.

Risorse addizionali

Come creare e interpretare box plot in Excel
Come creare e interpretare i box plot in SPSS
Come creare più box plot in R
Come creare e interpretare box plot in Stata