Come confrontare gli istogrammi (con esempi)

Un istogramma è un tipo di grafico che ci consente di visualizzare la distribuzione dei valori in un insieme di dati.

L’asse X mostra i valori del set di dati e l’asse Y mostra la frequenza di ciascun valore.

Gli istogrammi sono utili perché ci consentono di comprendere rapidamente la distribuzione dei valori in un set di dati. Sono utili anche per confrontare due diversi set di dati.

Quando confrontiamo due o più istogrammi, possiamo rispondere a tre diverse domande:

1. Come si confrontano i valori mediani?

Possiamo stimare approssimativamente che la mediana si trovi vicino al centro di ciascun istogramma, permettendoci di confrontare i valori mediani delle distribuzioni.

2. Come si confronta la dispersione?

Possiamo vedere visivamente quale istogramma è più disperso, il che ci dà un’idea di quale distribuzione ha valori più dispersi.

3. Come si confronta l’asimmetria?

Se un istogramma ha una “coda” sul lato sinistro del grafico, si dice che sia inclinato negativamente. Al contrario, se un istogramma ha una “coda” sul lato destro del grafico, si dice che sia inclinato positivamente. Possiamo controllare visivamente ciascun istogramma per confrontare l’asimmetria .

L’esempio seguente mostra come confrontare due diversi istogrammi e rispondere a queste tre domande.

Esempio: confronto degli istogrammi

Si presuppone che 200 studenti utilizzino un metodo di studio per prepararsi per un esame e altri 200 studenti utilizzino un metodo di studio diverso per prepararsi per lo stesso esame.

Supponiamo di creare i seguenti istogrammi per confrontare i risultati degli esami di ciascun gruppo di studenti:

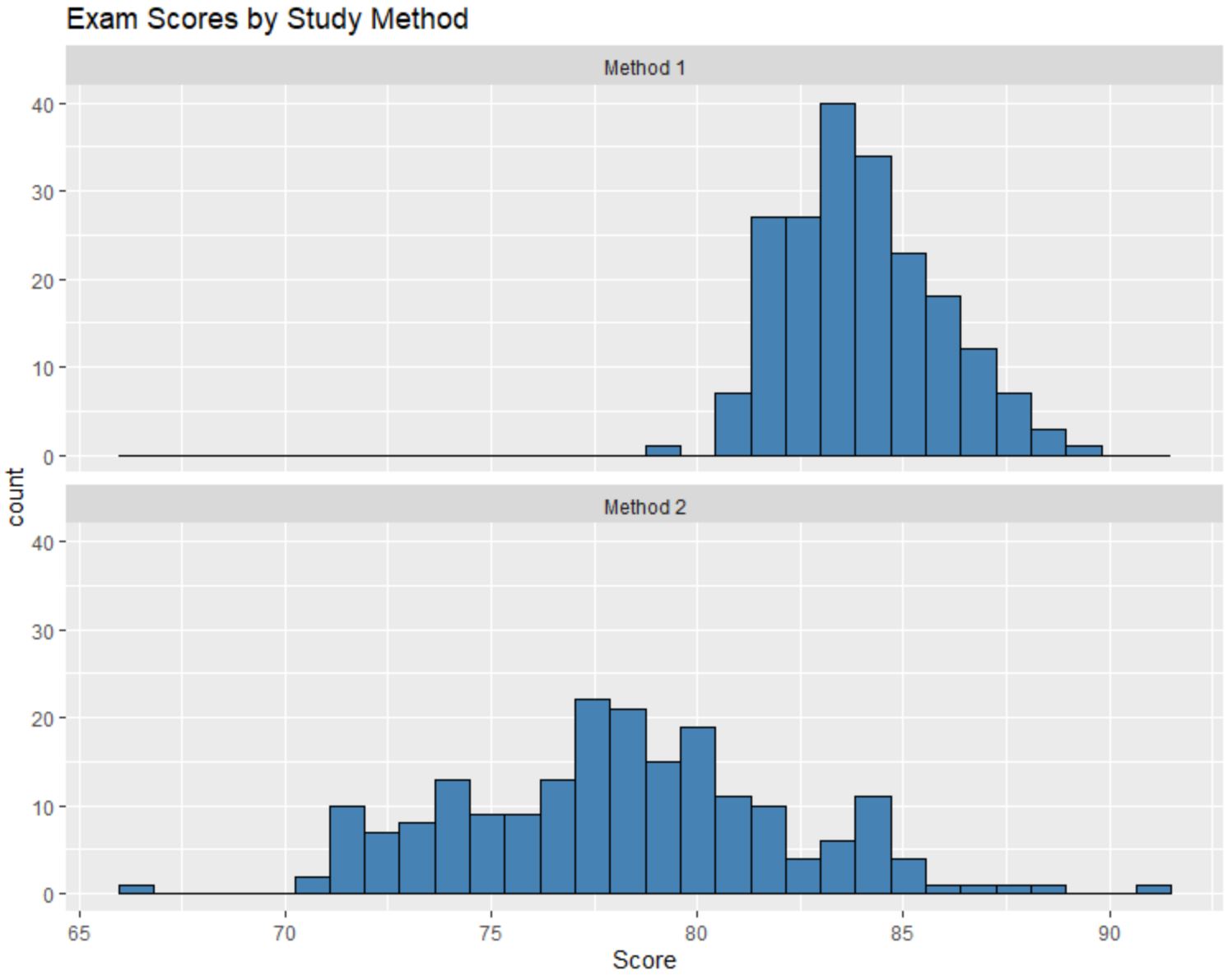
Possiamo confrontare questi istogrammi e rispondere alle seguenti tre domande:

1. Come si confrontano i valori mediani?

Sebbene non conosciamo gli esatti valori mediani di ciascuna distribuzione semplicemente osservando gli istogrammi, è ovvio che il punteggio medio dell’esame degli studenti che hanno utilizzato il Metodo 1 è superiore al punteggio medio dell’esame degli studenti che hanno utilizzato il Metodo 1. metodo 2.

Potremmo stimare che il valore mediano per il metodo 1 sia intorno a 84 e il valore mediano per il metodo 2 sia intorno a 78.

2. Come si confronta la dispersione?

I valori dell’istogramma per il Metodo 2 sono molto più dispersi rispetto a quelli per il Metodo 1, il che ci dice che c’è una dispersione molto maggiore nei risultati dell’esame per gli studenti che hanno utilizzato il Metodo 2.

3. Come si confronta l’asimmetria?

Osservando gli istogrammi, sembra che la distribuzione dei punteggi dei test per il Metodo 1 sia leggermente sbilanciata verso destra, come indicato dalla “coda” che si estende a destra dell’istogramma.

Tuttavia, non sembra esserci una “coda” nella distribuzione dei risultati degli esami per il metodo 2, il che ci dice che la distribuzione è poco o per nulla distorta.

Bonus : ecco il codice che abbiamo usato in R per creare questi due istogrammi:

 library (ggplot2)

#make this example reproducible
set. seeds (0)

#create data frame
df <- data. frame (method=rep(c(' Method 1 ', ' Method 2 '), each= 200 ),
                 Score=c(rnorm( 200 , mean= 84 , sd= 2 ),
                         rnorm( 200 , mean= 78 , sd= 4 )))

#create histogram of scores for each method
ggplot(df, aes(x=Score)) +
  geom_histogram(fill=' steelblue ', color=' black ') +
  facet_wrap(.~method, nrow= 2 ) +
  labs(title=' Exam Scores by Study Method ')

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni con gli istogrammi:

Come stimare la media e la mediana di qualsiasi istogramma
Come stimare la deviazione standard di qualsiasi istogramma
Come descrivere la forma degli istogrammi