Confronto dei punteggi z di diverse distribuzioni

Un punteggio z indica di quante deviazioni standard un singolo valore di dati cade dalla media. Viene calcolato come segue:

Punteggio z = (x – μ) / σ

Oro:

• x: valore del dato individuale
• μ: media della popolazione
• σ: deviazione standard della popolazione

Un punteggio z per un valore individuale può essere interpretato come segue:

• Z-score positivo: il valore individuale è superiore alla media.
• Z-score negativo: il valore individuale è inferiore alla media.
• Un punteggio z pari a 0: il valore individuale è uguale alla media.

I punteggi Z sono particolarmente utili quando vogliamo confrontare la posizione relativa di due punti dati di due diverse distribuzioni. Per illustrare ciò, si consideri il seguente esempio.

Esempio: confronto dei punteggi Z

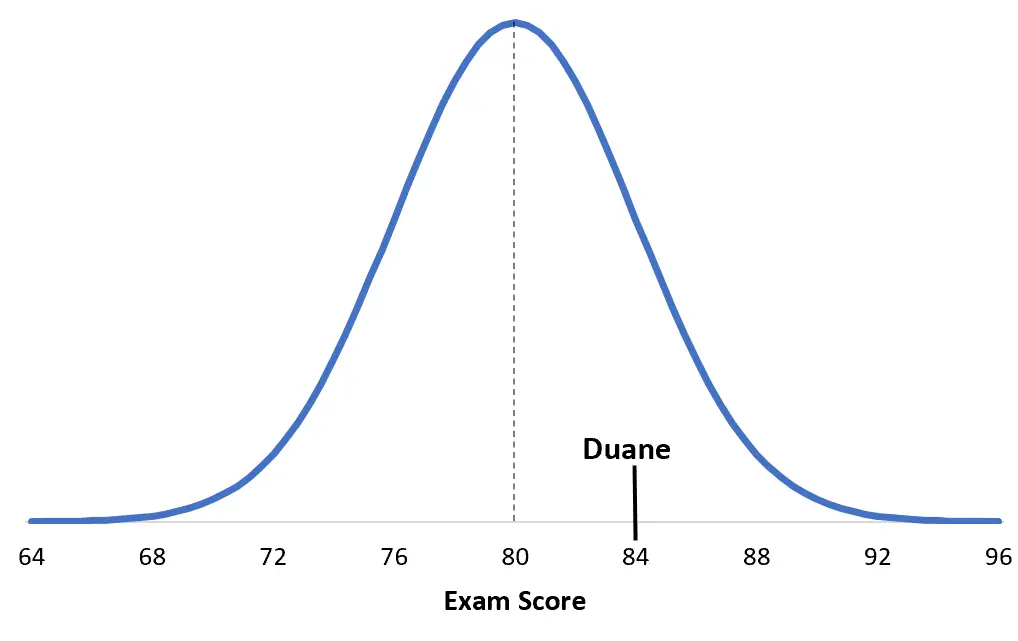
I punteggi di un determinato esame universitario sono normalmente distribuiti con media μ = 80 e deviazione standard σ = 4. Duane ottiene un punteggio di 84 in questo esame.

I punteggi di un altro esame universitario sono normalmente distribuiti con media μ = 85 e deviazione standard σ = 8. Debbie ottiene 90 in quell’esame.

Rispetto alla distribuzione dei punteggi degli esami, chi ha ottenuto i migliori risultati all’esame?

Per rispondere a questa domanda, possiamo calcolare lo z-score del punteggio dell’esame di ciascuna persona:

Punteggio z di Duane = (x – μ) / σ = (84 – 80) / 4 = 4 / 4 = 1

Punteggio z di Debbie = (x – μ) / σ = (90 – 85) / 8 = 5/8 = 0,625

Debbie Sebbene abbia ottenuto un punteggio più alto, il punteggio di Duane è in realtà più alto rispetto alla distribuzione del suo esame particolare.

Per capirlo è utile visualizzare la situazione. Ecco il punteggio di Duane rispetto alla sua particolare ripartizione dell’esame:

Ed ecco il punteggio di Debbie in base alla ripartizione dell’esame:

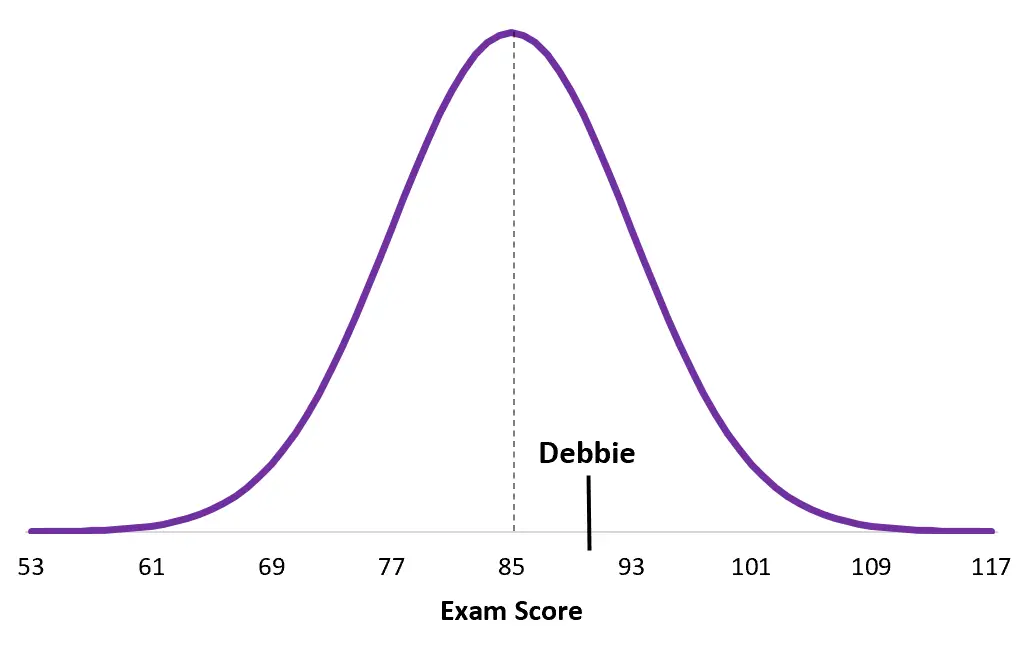
Nota quanto il punteggio di Debbie è più vicino alla media della sua popolazione rispetto a quello di Duane. Sebbene abbia un punteggio complessivo più alto, il suo punteggio z è più basso semplicemente perché il punteggio medio del suo esame particolare è più alto.

Questo esempio illustra perché i punteggi z sono così utili per confrontare i valori dei dati di diverse distribuzioni: i punteggi z tengono conto della media e delle deviazioni standard delle distribuzioni, il che ci consente di confrontare i valori dei dati di diverse distribuzioni e vedere quale è più alti rispetto alle loro distribuzioni.

Risorse addizionali

Calcolatore del punteggio Z
Confronta il calcolatore del punteggio Z