Come creare una matrice di confusione in r (passo dopo passo)

La regressione logistica è un tipo di regressione che possiamo utilizzare quando la variabile di risposta è binaria.

Un modo comune per valutare la qualità di un modello di regressione logistica è creare una matrice di confusione , ovvero una tabella 2 × 2 che mostra i valori previsti del modello rispetto ai valori effettivi del set di dati di test.

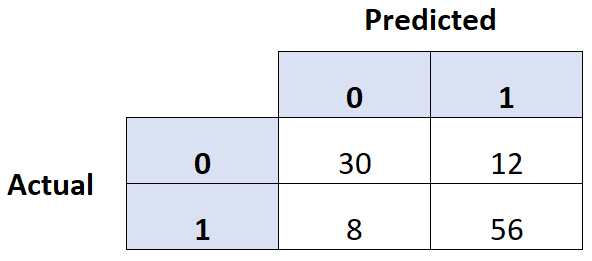
Il seguente esempio passo passo mostra come creare una matrice di confusione in R.

Passaggio 1: adattare il modello di regressione logistica

Per questo esempio utilizzeremo il set di dati predefinito del pacchetto ISLR . Utilizzeremo lo status di studente, il saldo bancario e il reddito annuo per prevedere la probabilità che una determinata persona non riesca a onorare il prestito.

Il codice seguente mostra come adattare un modello di regressione logistica a questo set di dati:

 #load necessary packages
library (caret)
library (InformationValue)
library (ISLR)

#load dataset
data <-Default

#split dataset into training and testing set
set. seeds (1)
sample <- sample(c(TRUE, FALSE), nrow(data), replace= TRUE , prob=c(0.7,0.3))
train <- data[sample, ]
test <- data[!sample, ]

#fit logistic regression model
model <- glm(default~student+balance+income, family=" binomial ", data=train)

Passaggio 2: crea la matrice di confusione

Successivamente, utilizzeremo la funzione confusionMatrix() dal pacchetto caret per creare una matrice di confusione:

 #use model to predict probability of default
predicted <- predict(model, test, type="response")

#convert defaults from "Yes" and "No" to 1's and 0's
test$default <- ifelse(test$default==" Yes ", 1, 0)

#find optimal cutoff probability to use to maximize accuracy
optimal <- optimalCutoff(test$default, predicted)[1]

#create confusion matrix
confusionMatrix(test$default, predicted)

     0 1
0 2912 64
1 21 39

Passaggio 3: valutare la matrice di confusione

Possiamo anche calcolare le seguenti metriche utilizzando la matrice di confusione:

• Sensibilità: il “vero tasso di positività” – la percentuale di individui che il modello aveva previsto correttamente sarebbero andati in default.
• Specificità: il “vero tasso negativo” – la percentuale di individui che il modello aveva previsto correttamente non sarebbero andati in default.
• Tasso di classificazione errata totale: percentuale del totale di classificazioni errate effettuate dal modello.

Il codice seguente mostra come calcolare queste metriche:

 #calculate sensitivity
sensitivity(test$default, predicted)

[1] 0.3786408

#calculate specificity
specificity(test$default, predicted)

[1] 0.9928401

#calculate total misclassification error rate
misClassError(test$default, predicted, threshold =optimal)

[1] 0.027

Il tasso di errore di classificazione totale è del 2,7% per questo modello.

In generale, più basso è questo tasso, migliore è la capacità del modello di prevedere i risultati. Questo particolare modello si rivela quindi molto efficace nel prevedere se un individuo andrà in default o meno.