Come calcolare la correlazione incrociata in r

La correlazione incrociata è un modo per misurare il grado di somiglianza tra una serie temporale e una versione ritardata di un’altra serie temporale.

Questo tipo di correlazione è utile da calcolare perché può dirci se i valori in una serie temporale sono predittivi dei valori futuri in un’altra serie temporale. In altre parole, può dirci se una serie temporale è un indicatore anticipatore per un’altra serie temporale.

Questo tipo di correlazione viene utilizzato in molti campi diversi, tra cui:

Economia: l’indice della fiducia dei consumatori (CCI) è considerato un indicatore anticipatore del prodotto interno lordo (PIL) di un paese. Ad esempio, se il CCI è elevato in un dato mese, è probabile che il PIL sarà più alto x mesi dopo.

Imprese: le spese di marketing sono spesso considerate un indicatore importante delle future entrate aziendali. Ad esempio, se un’azienda spende una somma di denaro insolitamente elevata per il marketing in un trimestre, i ricavi totali dovrebbero essere elevati x trimestri successivi.

Biologia: l’inquinamento totale dell’oceano è considerato un indicatore importante della popolazione di una determinata specie di tartaruga. Ad esempio, se l’inquinamento è maggiore in un dato anno, si prevede che la popolazione totale delle tartarughe diminuirà x anni dopo.

L’esempio seguente mostra come calcolare la correlazione incrociata tra due serie temporali in R.

Esempio: come calcolare la correlazione incrociata in R

Supponiamo di avere la seguente serie temporale in R che mostra la spesa totale di marketing (in migliaia) per una determinata azienda e le entrate totali (in migliaia) per 12 mesi consecutivi:

 #define data
marketing <- c(3, 4, 5, 5, 7, 9, 13, 15, 12, 10, 8, 8)
revenue <- c(21, 19, 22, 24, 25, 29, 30, 34, 37, 40, 35, 30)

Possiamo calcolare la correlazione incrociata per ogni ritardo tra le due serie temporali utilizzando la funzione ccf() come segue:

 #calculate cross correlation
ccf(marketing, revenue)

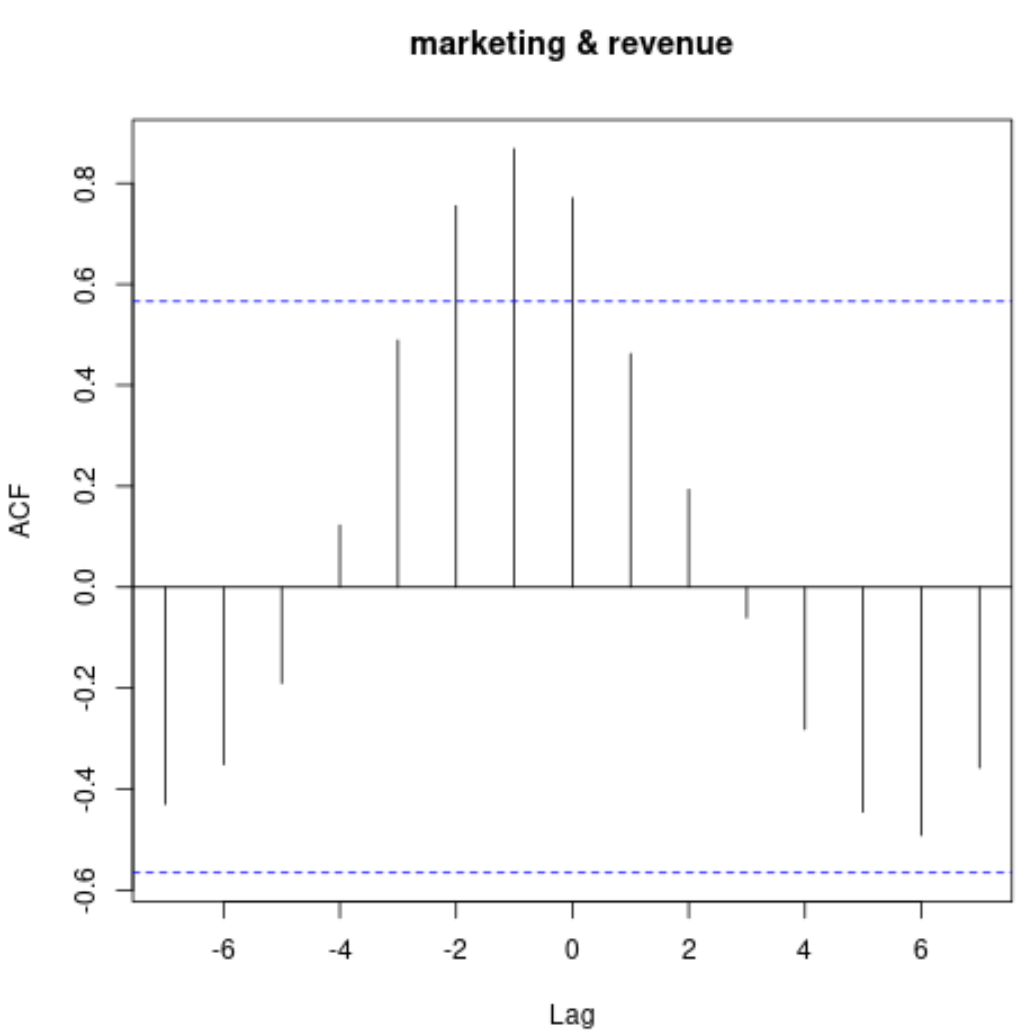
Questo grafico mostra la correlazione tra le due serie temporali con ritardi diversi.

Per visualizzare i valori di correlazione effettivi, possiamo utilizzare la seguente sintassi:

 #display cross correlation values
print (ccf(marketing, revenue))

Autocorrelations of series 'X', by lag

    -7 -6 -5 -4 -3 -2 -1 0 1 2 3 
-0.430 -0.351 -0.190 0.123 0.489 0.755 0.868 0.771 0.462 0.194 -0.061 
     4 5 6 7 
-0.282 -0.445 -0.492 -0.358

Ecco come interpretare questo output:

• La correlazione incrociata al ritardo 0 è 0,771 .
• La correlazione incrociata al ritardo 1 è 0,462 .
• La correlazione incrociata al ritardo 2 è 0,194 .
• La correlazione incrociata al ritardo 3 è -0,061 .

E così via.

Si noti che la correlazione tra le due serie temporali è abbastanza positiva con ritardi compresi tra -2 e 2, il che ci dice che la spesa di marketing in un dato mese è abbastanza predittiva delle entrate uno e due mesi dopo.

Ciò ha un senso intuitivo: prevediamo che un’elevata spesa di marketing in un dato mese sarà predittiva di un aumento delle entrate nei prossimi due mesi.

Risorse addizionali

Come calcolare l’autocorrelazione in R
Come calcolare la correlazione parziale in R
Come calcolare la correlazione scorrevole in R