Come calcolare la correlazione tra variabili categoriali

Usiamo spesso il coefficiente di correlazione di Pearson per calcolare la correlazione tra variabili numeriche continue.

Dobbiamo però utilizzare una metrica diversa per calcolare la correlazione tra variabili categoriali, ovvero variabili che assumono nomi o etichette come:

• Stato civile (celibe, sposato, divorziato)
• Stato di fumatore (fumatore, non fumatore)
• Colore degli occhi (blu, marrone, verde)

Esistono tre misure comunemente utilizzate per calcolare la correlazione tra variabili categoriali:

1. Correlazione tetracorica: utilizzata per calcolare la correlazione tra variabili categoriche binarie.

2. Correlazione policorica: utilizzata per calcolare la correlazione tra variabili categoriche ordinali.

3. V di Cramer: utilizzato per calcolare la correlazione tra variabili categoriali nominali.

Le sezioni seguenti forniscono un esempio di come calcolare ciascuna di queste tre misurazioni.

Metrica 1: correlazione tetracorica

La correlazione tetracorica viene utilizzata per calcolare la correlazione tra variabili categoriche binarie. Ricorda che le variabili binarie sono variabili che possono assumere solo uno dei due valori possibili.

Il valore di correlazione tetracorica varia da -1 a 1, dove -1 indica una forte correlazione negativa, 0 indica alcuna correlazione e 1 indica una forte correlazione positiva.

Ad esempio, supponiamo di voler sapere se il genere è associato o meno alla preferenza per un partito politico. Quindi prendiamo un semplice campione casuale di 100 elettori e chiediamo loro quale sia la loro preferenza per un partito politico.

La tabella seguente presenta i risultati dell’indagine:

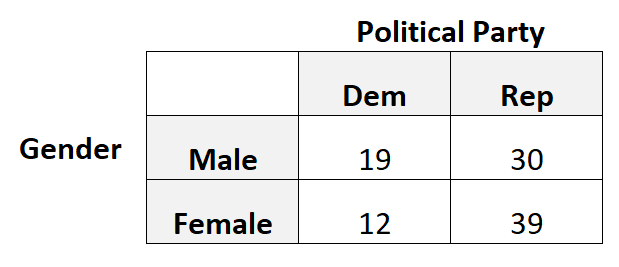
Utilizzeremmo la correlazione tetracorica in questo scenario perché ciascuna variabile categoriale è binaria, ovvero ciascuna variabile può assumere solo due valori possibili.

Possiamo usare il seguente codice in R per calcolare la correlazione tetracorica tra le due variabili:

 library (psych)

#create 2x2 table
data = matrix(c(19, 12, 30, 39), nrow= 2 )

#view table
data

#calculate tetrachoric correlation
tetrachoric(data)

tetrachoric correlation 
[1] 0.27

La correlazione tetracorica risulta essere 0,27 . Questo valore è piuttosto basso, indicando che esiste una debole (se presente) associazione tra genere e preferenza del partito politico.

Metrica 2: correlazione policorica

La correlazione policorica viene utilizzata per calcolare la correlazione tra variabili categoriche ordinali. Ricordiamo che le variabili ordinali sono variabili i cui possibili valori hanno un ordine naturale.

Il valore di correlazione policorica varia da -1 a 1, dove -1 indica una forte correlazione negativa, 0 indica nessuna correlazione e 1 indica una forte correlazione positiva.

Ad esempio, supponiamo che tu voglia sapere se due diverse agenzie di valutazione dei film hanno un’elevata correlazione tra le loro valutazioni dei film.

Chiediamo a ciascuna agenzia di valutare 20 film diversi su una scala da 1 a 3, dove 1 indica “cattivo”, 2 indica “scarso” e 3 indica “buono”.

La tabella seguente mostra i risultati:

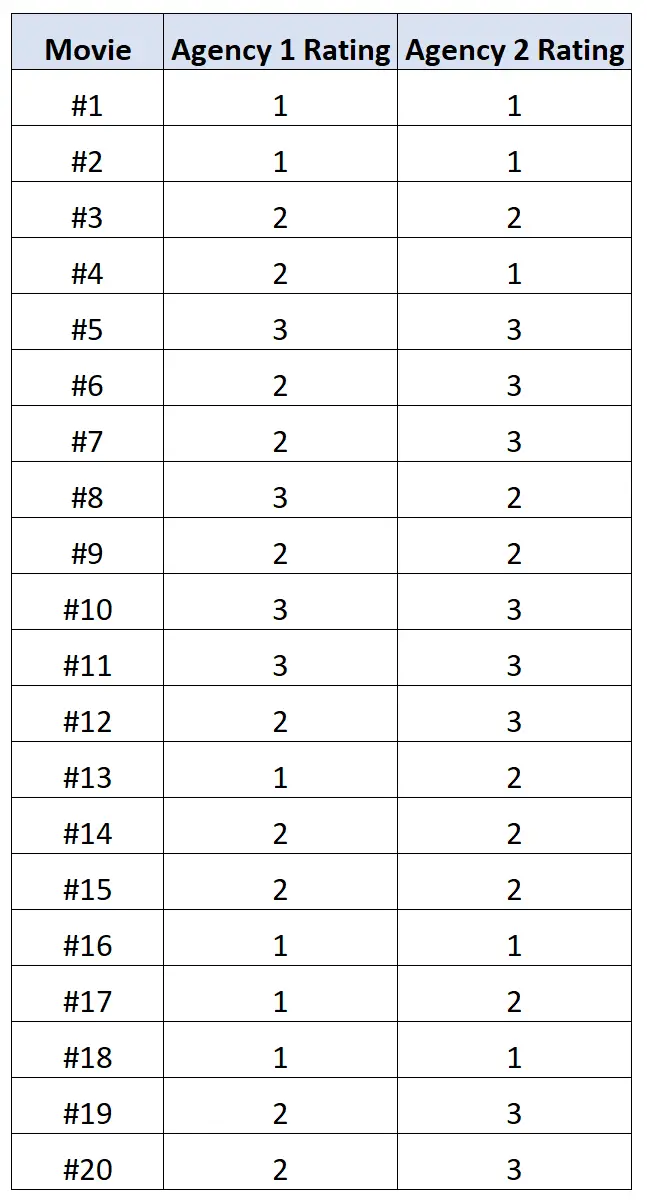
Possiamo utilizzare il seguente codice in R per calcolare la correlazione policorica tra i rating delle due agenzie:

 library (polycor)

#define movie ratings
x <- c(1, 1, 2, 2, 3, 2, 2, 3, 2, 3, 3, 2, 1, 2, 2, 1, 1, 1, 2, 2)
y <- c(1, 1, 2, 1, 3, 3, 3, 2, 2, 3, 3, 3, 2, 2, 2, 1, 2, 1, 3, 3)

#calculate polychoric correlation between ratings
polychor(x, y)

[1] 0.7828328

La correlazione policorica risulta essere 0,78 . Questo valore è piuttosto elevato, il che indica che esiste una forte associazione positiva tra i rating di ciascuna agenzia.

Metrica 3: V di Cramer

La V di Cramer viene utilizzata per calcolare la correlazione tra variabili categoriali nominali. Ricorda che le variabili nominali sono quelle che portano etichette di categoria ma non hanno un ordine naturale.

Il valore della V di Cramer varia da 0 a 1, dove 0 indica nessuna associazione tra le variabili e 1 indica una forte associazione tra le variabili.

Ad esempio, supponiamo di voler sapere se esiste una correlazione tra il colore degli occhi e il sesso. Interroghiamo quindi 50 persone e otteniamo i seguenti risultati:

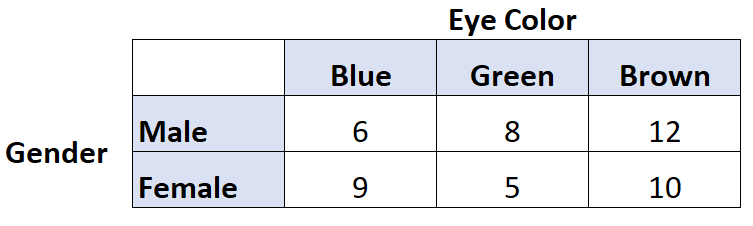
Possiamo usare il seguente codice in R per calcolare la V di Cramer per queste due variabili:

 library (rcompanion)

#create table
data = matrix(c(6, 9, 8, 5, 12, 10), nrow= 2 )

#view table
data

     [,1] [,2] [,3]
[1,] 6 8 12
[2,] 9 5 10

#calculate Cramer's V
cramerV(data)

Cramer V 
  0.1671

La V di Cramer risulta essere 0,1671 . Questo valore è piuttosto basso, indicando che esiste una debole associazione tra sesso e colore degli occhi.

Risorse addizionali

Introduzione al coefficiente di correlazione di Pearson
Introduzione alla correlazione tetracorica
Variabili categoriali o quantitative: qual è la differenza?
Livelli di misura: nominale, ordinale, intervallo e rapporto