Come calcolare la correlazione tra variabili continue e categoriali

Quando vogliamo calcolare la correlazione tra due variabili continue, generalmente utilizziamo il coefficiente di correlazione di Pearson .

Tuttavia, quando vogliamo calcolare la correlazione tra una variabile continua e una variabile categoriale , possiamo utilizzare quella che viene chiamata correlazione biseriale puntuale .

La correlazione biseriale puntuale viene utilizzata per calcolare la correlazione tra una variabile categoriale binaria (una variabile che può assumere solo due valori) e una variabile continua e ha le seguenti proprietà:

• La correlazione punto-biseriale può variare tra -1 e 1.
• Per ciascun gruppo creato dalla variabile binaria, si assume che la variabile continua sia normalmente distribuita con varianze uguali.
• Per ciascun gruppo creato dalla variabile binaria, si presuppone che non vi siano valori anomali estremi.

L’esempio seguente mostra come calcolare nella pratica una correlazione punto-biseriale.

Esempio: Calcolo di una correlazione punto-biseriale

Supponiamo che un professore universitario voglia determinare se esiste una correlazione tra genere e punteggio in un particolare esame di qualificazione.

Raccoglie i seguenti dati su 12 ragazzi e 12 ragazze della sua classe:

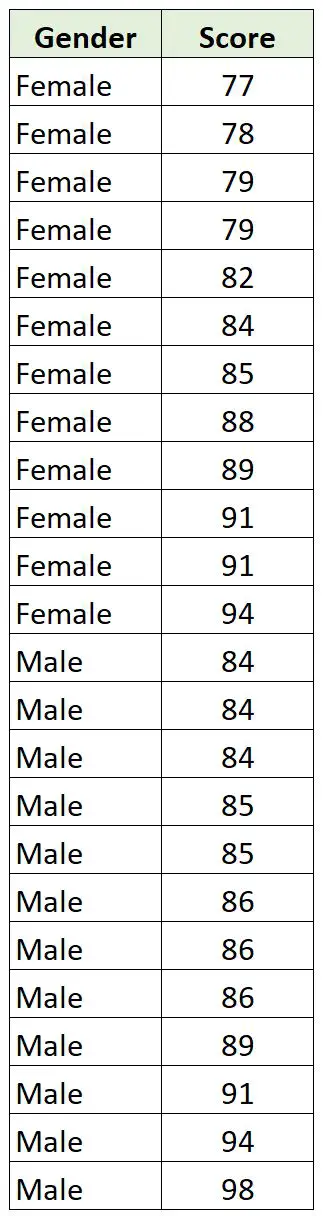
Poiché il genere è una variabile categoriale e il punteggio è una variabile continua, ha senso calcolare una correlazione punto-biseriale tra le due variabili.

Il docente può utilizzare qualsiasi software statistico (tra cui Excel, R, Python, SPSS, Stata) per calcolare la correlazione punto-biseriale tra le due variabili.

Il codice seguente mostra come calcolare la correlazione punto-biseriale in R, utilizzando il valore 0 per rappresentare le femmine e 1 per rappresentare i maschi per la variabile genere:

 #define values for gender
gender <- c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
            1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1)

#define values for score
score <- c(77, 78, 79, 79, 82, 84, 85, 88, 89, 91, 91, 94,
           84, 84, 84, 85, 85, 86, 86, 86, 89, 91, 94, 98)

#calculate point-biserial correlation
horn. test (gender, score)

	Pearson's product-moment correlation

data: gender and score
t = 1.3739, df = 22, p-value = 0.1833
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.1379386 0.6147832
sample estimates:
      horn 
0.2810996

Dal risultato, possiamo vedere che il coefficiente di correlazione punto-biseriale è 0,281 e il corrispondente valore p è 0,1833 .

Poiché il coefficiente di correlazione è positivo, ciò ci dice che esiste una correlazione positiva tra genere e punteggio.

Poiché abbiamo codificato i maschi come 1 e le femmine come 0, ciò indica che i punteggi tendono ad essere più alti per i maschi (cioè, i punteggi tendono ad aumentare man mano che il genere “aumenta”). » da 0 a 1).

Tuttavia, poiché il valore p non è inferiore a 0,05, questo coefficiente di correlazione non è statisticamente significativo.

Risorse addizionali

I seguenti tutorial spiegano come calcolare la correlazione biseriale dei punti utilizzando diversi software statistici:

Come calcolare la correlazione punto-biseriale in Excel
Come calcolare la correlazione punto-biseriale in R
Come calcolare la correlazione punto-biseriale in Python