Correlazione vs regressione: qual è la differenza?

Correlazione e regressione sono due termini statistici correlati, ma non del tutto identici.

In questo tutorial, forniremo una breve spiegazione di entrambi i termini e spiegheremo come sono simili e diversi.

Cos’è la correlazione?

La correlazione misura l’ associazione lineare tra due variabili, xey . Ha un valore compreso tra -1 e 1 dove:

• -1 indica una correlazione lineare perfettamente negativa tra due variabili
• 0 indica alcuna correlazione lineare tra due variabili
• 1 indica una correlazione lineare perfettamente positiva tra due variabili

Ad esempio, supponiamo di avere il seguente set di dati che contiene due variabili: (1) Ore studiate e (2) Punteggi degli esami ricevuti per 20 studenti diversi:

Se creassimo un grafico a dispersione delle ore studiate rispetto ai risultati degli esami, ecco come apparirebbe:

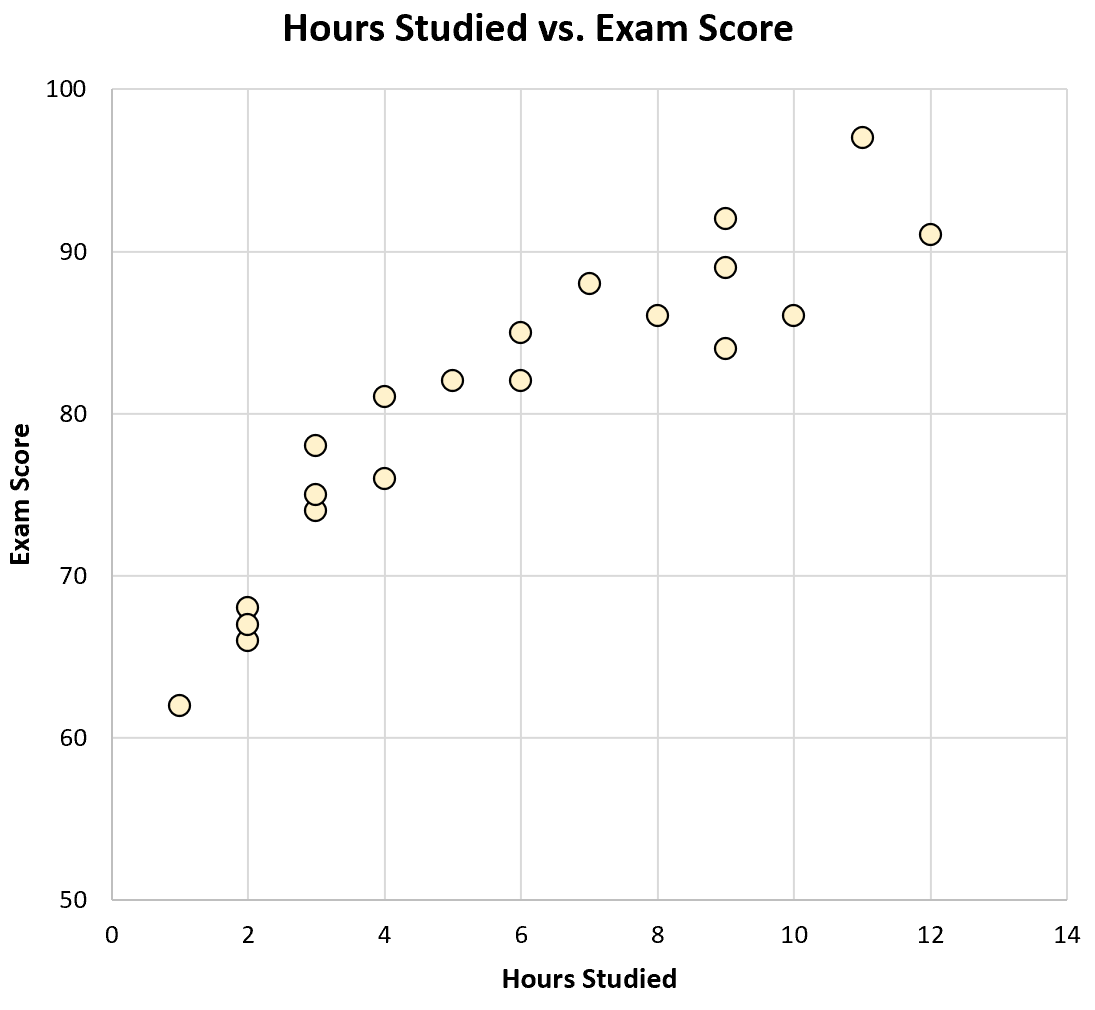
Basta osservare il grafico per notare che gli studenti che studiano di più tendono ad ottenere risultati migliori agli esami. In altre parole, possiamo vedere visivamente che esiste una correlazione positiva tra le due variabili.

Usando una calcolatrice, possiamo vedere che la correlazione tra queste due variabili è r = 0,915 . Questo valore essendo vicino a 1, conferma che esiste una forte correlazione positiva tra le due variabili.

Cos’è la regressione?

La regressione è un metodo che possiamo utilizzare per capire come la modifica dei valori della variabile x influisce sui valori della variabile y .

Un modello di regressione utilizza una variabile, x , come variabile predittrice e l’altra variabile, y , come variabile di risposta . Trova quindi un’equazione della forma seguente che meglio descrive la relazione tra le due variabili:

ŷ = b ₀ + b ₁ x

Oro:

• ŷ: il valore previsto della variabile di risposta
• b ₀ : L’ordinata all’origine (il valore di y quando x è uguale a zero)
• b ₁ : Il coefficiente di regressione (l’aumento medio di y per un aumento di un’unità di x)
• x: il valore della variabile predittiva

Ad esempio, considera il nostro set di dati precedente:

Utilizzando un calcolatore di regressione lineare , troviamo che la seguente equazione descrive meglio la relazione tra queste due variabili:

Punteggio previsto dell’esame = 65,47 + 2,58*(ore studiate)

Il modo di interpretare questa equazione è:

• Il punteggio previsto per l’esame per uno studente che studia a zero ore è 65,47 .
• L’aumento medio del punteggio dell’esame associato ad un’ora aggiuntiva di studio è 2,58 .

Possiamo anche usare questa equazione per prevedere il punteggio che uno studente riceverà in base al numero di ore studiate.

Ad esempio, uno studente che studia 6 ore dovrebbe ricevere un voto di 80,95 :

Punteggio previsto dell’esame = 65,47 + 2,58*(6) = 80,95 .

Possiamo anche tracciare questa equazione come una linea su un grafico a dispersione:

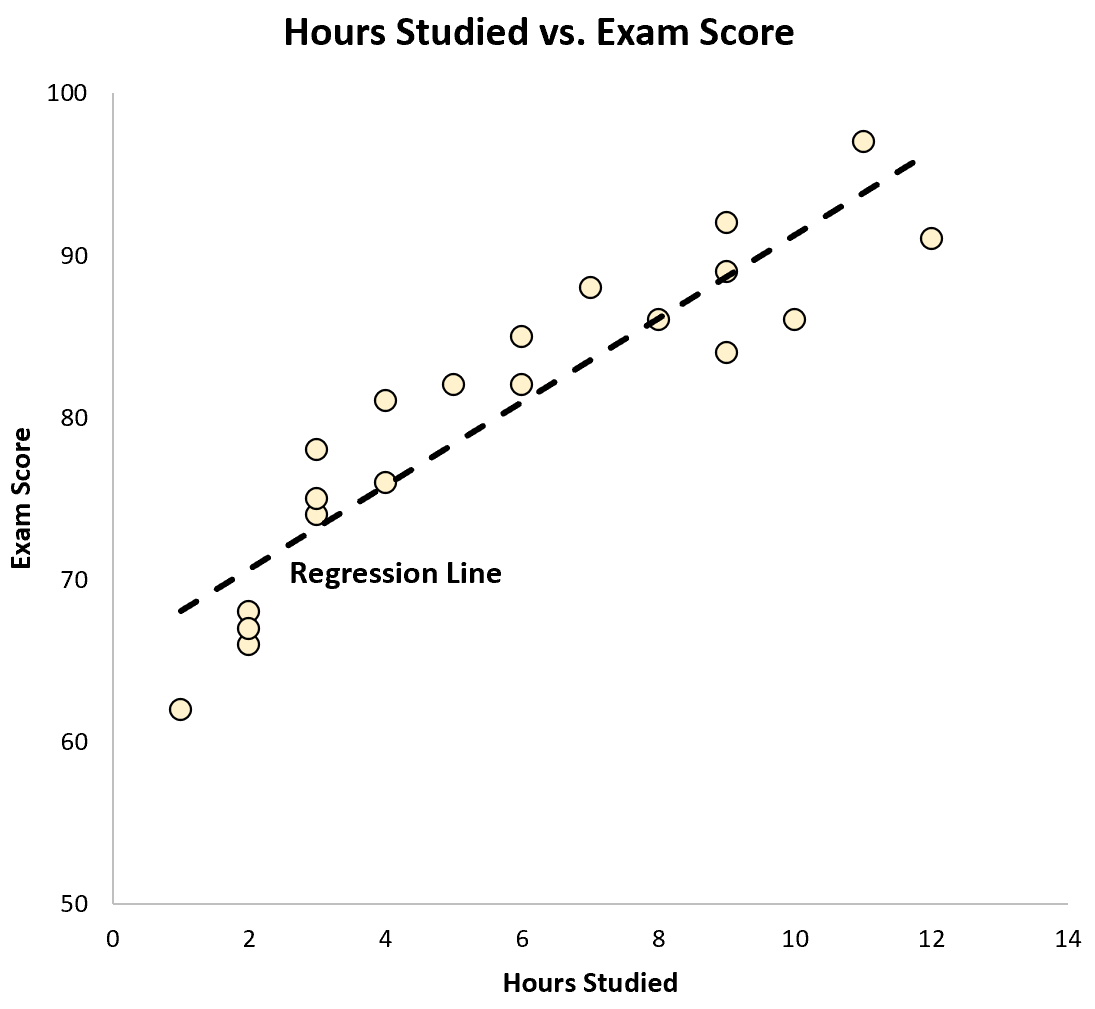
Possiamo vedere che la retta di regressione “si adatta” abbastanza bene ai dati.

Ricordiamo in precedenza che la correlazione tra queste due variabili era r = 0,915 . Risulta che possiamo elevare al quadrato questo valore e ottenere un numero chiamato “r al quadrato” che descrive la proporzione totale della varianza nella variabile di risposta che può essere spiegata dalla variabile predittore.

In questo esempio, r ² = 0,915 ² = 0,837 . Ciò significa che l’83,7% della variazione dei punteggi degli esami può essere spiegata dal numero di ore studiate.

Correlazione vs regressione: somiglianze e differenze

Ecco un riepilogo delle somiglianze e delle differenze tra correlazione e regressione:

Analogie:

• Entrambi quantificano la direzione di una relazione tra due variabili.
• Entrambi quantificano la forza di una relazione tra due variabili.

Differenze:

• La regressione è in grado di mostrare una relazione di causa ed effetto tra due variabili. La correlazione non fa questo.
• La regressione è in grado di utilizzare un’equazione per prevedere il valore di una variabile, in base al valore di un’altra variabile. La correlazione non fa questo.
• La regressione utilizza un’equazione per quantificare la relazione tra due variabili. La correlazione utilizza un singolo numero.

Risorse addizionali

I seguenti tutorial offrono spiegazioni più approfondite degli argomenti trattati in questo articolo.

Un’introduzione al coefficiente di correlazione di Pearson
Un’introduzione alla regressione lineare semplice
Semplice calcolatore di regressione lineare
Qual è un buon valore di R quadrato?