Correlazioni in stata: pearson, spearman e kendall

In statistica, la correlazione si riferisce alla forza e alla direzione di una relazione tra due variabili. Il valore di un coefficiente di correlazione può variare da -1 a 1, dove -1 indica una relazione negativa perfetta, 0 indica nessuna relazione e 1 indica una relazione positiva perfetta.

Esistono tre modi comuni per misurare la correlazione:

Correlazione di Pearson: utilizzata per misurare la correlazione tra due variabili continue. (ad esempio altezza e peso)

Correlazione di Spearman: utilizzata per misurare la correlazione tra due variabili classificate. (ad esempio, la classifica del punteggio dell’esame di matematica di uno studente rispetto alla classifica del punteggio dell’esame di scienze in una classe)

Correlazione di Kendall: utilizzata quando si desidera utilizzare la correlazione di Spearman ma la dimensione del campione è piccola e sono presenti molte classifiche correlate.

Questo tutorial spiega come trovare i tre tipi di correlazioni in Stata.

Caricamento dati

Per ciascuno dei seguenti esempi, utilizzeremo un set di dati chiamato auto . È possibile caricare questo set di dati digitando quanto segue nella casella Comando:

utilizzare https://www.stata-press.com/data/r13/auto

Possiamo avere una rapida panoramica del set di dati digitando quanto segue nella casella di comando:

riassumere

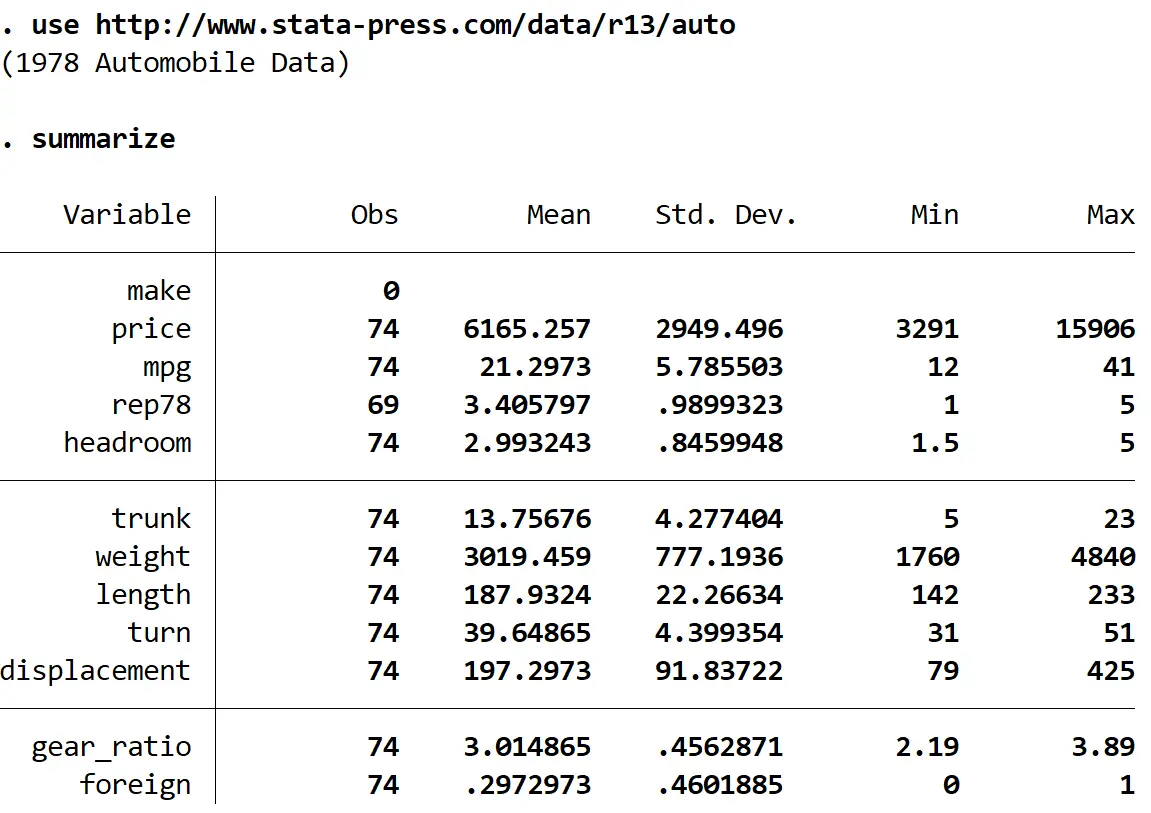
Possiamo vedere che ci sono 12 variabili in totale nel set di dati.

Come trovare la correlazione di Pearson in Stata

Possiamo trovare il coefficiente di correlazione di Pearson tra le variabili peso e lunghezza utilizzando il comando pwcorr :

lunghezza del peso pwcorr

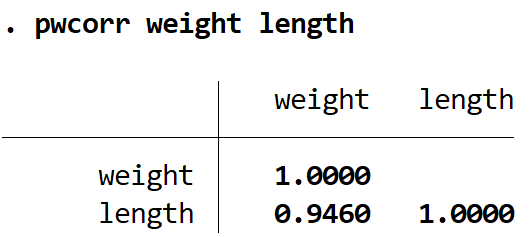
Il coefficiente di correlazione di Pearson tra queste due variabili è 0,9460 . Per determinare se questo coefficiente di correlazione è significativo, possiamo trovare il valore di p utilizzando il comando sig :

pwcorr peso lunghezza, sig

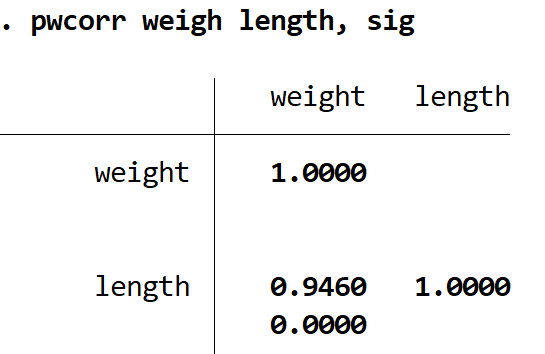
Il valore p è 0,000 . Poiché questo è inferiore a 0,05, la correlazione tra queste due variabili è statisticamente significativa.

Per trovare il coefficiente di correlazione di Pearson per più variabili, digita semplicemente un elenco di variabili dopo il comando pwcorr :

pwcorr peso lunghezza spostamento, sig

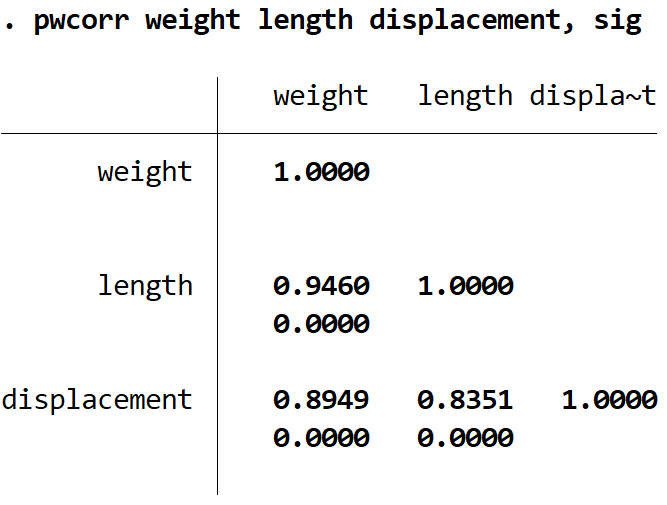
Ecco come interpretare il risultato:

• Correlazione di Pearson tra peso e lunghezza = 0,9460 | valore p = 0,000
• Correlazione di Pearson tra peso e spostamento = 0,8949 | valore p = 0,000
• Correlazione di Pearson tra spostamento e lunghezza = 0,8351 | valore p = 0,000

Come trovare la correlazione di Spearman in Stata

Possiamo trovare il coefficiente di correlazione di Spearman tra le variabili trunk e rep78 utilizzando il comando spearman :

lancia tronco rep78

Ecco come interpretare il risultato:

• Numero di osservazioni: questo è il numero di osservazioni a coppie utilizzate per calcolare il coefficiente di correlazione di Spearman. Poiché mancavano alcuni valori per la variabile rep78 , Stata ha utilizzato solo 69 osservazioni per coppia (invece delle 74 complete).
• Rho di Spearman: questo è il coefficiente di correlazione di Spearman. In questo caso è -0,2235, il che indica che esiste una correlazione negativa tra le due variabili. All’aumentare dell’uno l’altro tende a diminuire.
• Prob > |t| : Questo è il valore p associato al test di ipotesi. In questo caso, il valore p è 0,0649, il che indica che non esiste una correlazione statisticamente significativa tra le due variabili a α = 0,05.

Possiamo trovare il coefficiente di correlazione di Spearman per più variabili semplicemente digitando più variabili dopo il comando Spearman . Possiamo trovare il coefficiente di correlazione e il corrispondente valore p per ciascuna correlazione a coppie utilizzando il comando stats(rho p) :

spearman trunk rep78 gear_ratio, statistiche (rho p)

Ecco come interpretare il risultato:

• Correlazione di Spearman tra tronco e rep78 = -0,2235 | valore p = 0,0649
• Correlazione di Spearman tra trunk e gear_ratio = -0,5187 | valore p = 0,0000
• Correlazione di Spearman tra gear_ratio e rep78 = 0,4275 | valore p = 0,0002

Come trovare la correlazione di Kendall in Stata

Possiamo trovare il coefficiente di correlazione Kendall tra le variabili trunk e rep78 utilizzando il comando ktau :

ktau tronco rep78

Ecco come interpretare il risultato:

• Numero di osservazioni: questo è il numero di osservazioni a coppie utilizzate per calcolare il coefficiente di correlazione di Kendall. Poiché mancavano alcuni valori per la variabile rep78 , Stata ha utilizzato solo 69 osservazioni per coppia (invece delle 74 complete).
• Tau-b di Kendall: questo è il coefficiente di correlazione di Kendall tra le due variabili. Generalmente utilizziamo questo valore invece di tau-a perché tau-b apporta aggiustamenti in caso di parità. In questo caso, tau-b = -0,1752, indicando una correlazione negativa tra le due variabili.
• Problema > |z| : Questo è il valore p associato al test di ipotesi. In questo caso, il valore p è 0,0662, il che indica che non esiste una correlazione statisticamente significativa tra le due variabili a α = 0,05.

Possiamo trovare il coefficiente di correlazione di Kendall per più variabili semplicemente digitando più variabili dopo il comando ktau . Possiamo trovare il coefficiente di correlazione e il corrispondente valore p per ciascuna correlazione a coppie utilizzando il comando stats(taub p) :

ktau trunk rep78 gear_ratio, statistiche (taub p)

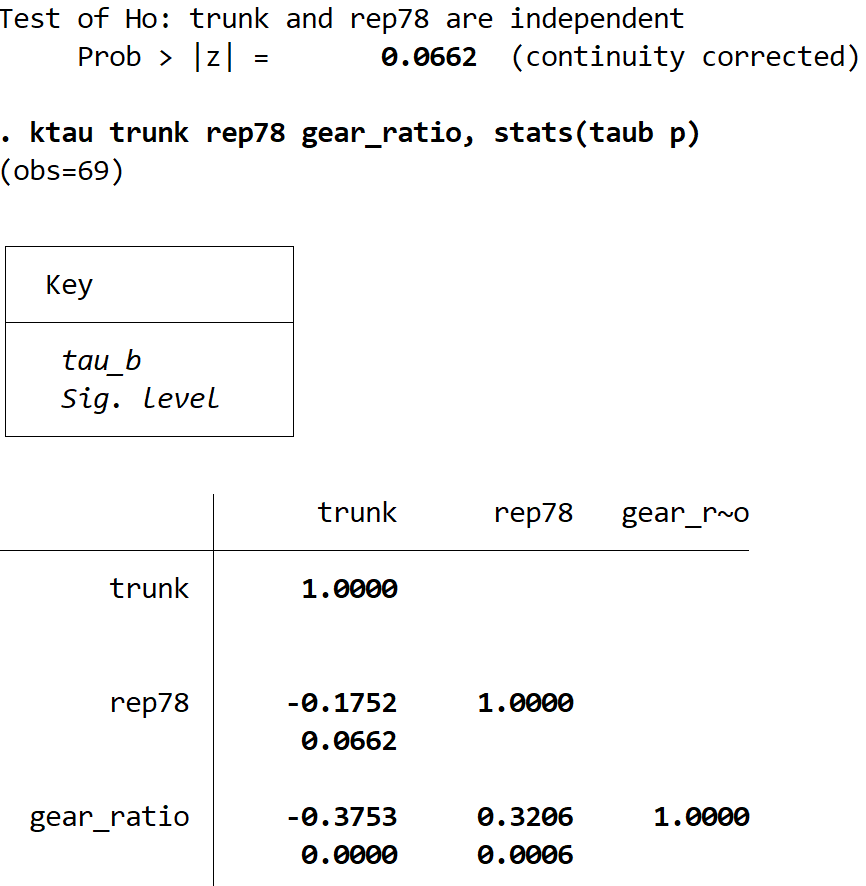
• Correlazione Kendall tra tronco e rep78 = -0,1752 | valore p = 0,0662
• Correlazione di Kendall tra trunk e gear_ratio = -0,3753 | valore p = 0,0000
• Correlazione Kendall tra gear_ratio e rep78 = 0,3206 | valore p = 0,0006