Una semplice spiegazione della correzione di continuità nelle statistiche
La correzione della continuità viene applicata quando si desidera utilizzare una distribuzione continua per approssimare una distribuzione discreta. Generalmente viene utilizzato quando si desidera utilizzare una distribuzione normale per approssimare una distribuzione binomiale .
Ricordiamo che la distribuzione binomiale ci dice la probabilità di ottenere x successo in n prove, dato che la probabilità di successo in una singola prova è p . Per rispondere a domande sulla probabilità con una distribuzione binomiale, potremmo semplicemente utilizzare un calcolatore di distribuzione binomiale , ma potremmo anche approssimare la probabilità utilizzando una distribuzione normale con una correzione di continuità.
Una correzione di continuità è il nome dato all’aggiunta o alla sottrazione di 0,5 da un valore x discreto .
Ad esempio, supponiamo di voler trovare la probabilità che una moneta esca testa inferiore o uguale a 45 volte nel corso di 100 lanci. Vogliamo cioè trovare P(X ≤ 45). Per utilizzare la distribuzione normale per approssimare la distribuzione binomiale, troveremmo invece P(X ≤ 45,5).
La tabella seguente mostra quando dovresti aggiungere o sottrarre 0,5, a seconda del tipo di probabilità che stai cercando di trovare:
| Utilizza la distribuzione binomiale | Utilizzando la distribuzione normale con correzione di continuità |
|---|---|
| X = 45 | 44,5 < X < 45,5 |
| X ≤ 45 | X<45,5 |
| X<45 | X<44,5 |
| X≥ 45 | X > 44,5 |
| X > 45 | X > 45,5 |
Nota:
È opportuno applicare una correzione di continuità alla distribuzione normale per approssimare la distribuzione binomiale solo quando n*p e n*(1-p) sono entrambi almeno 5.
Ad esempio, supponiamo n = 15 e p = 0,6. In questo caso:
n*p = 15 * 0,6 = 9
n*(1-p) = 15 * (1 – 0,6) = 15 * (0,4) = 6
Poiché entrambi questi numeri sono maggiori o uguali a 5, in questo scenario sarebbe accettabile applicare una correzione di continuità.
L’esempio seguente illustra come applicare una correzione di continuità alla distribuzione normale per approssimare la distribuzione binomiale.
Esempio di applicazione della correzione di continuità
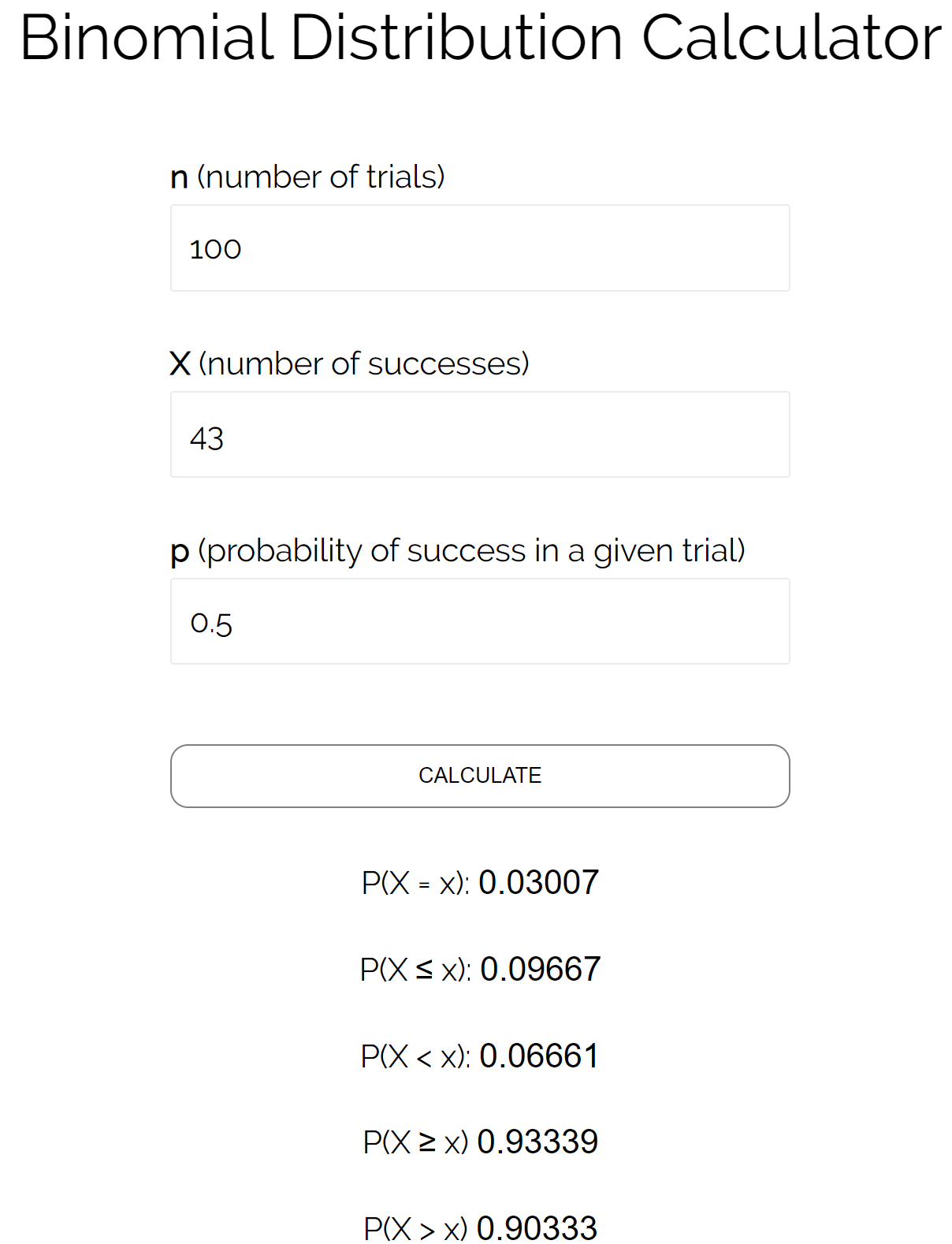
Supponiamo di voler conoscere la probabilità che una moneta esca testa minore o uguale a 43 volte in 100 lanci. In questo caso:
n = numero di prove = 100
X = numero di successi = 43
p = probabilità di successo in una determinata prova = 0,50
Possiamo inserire questi numeri nel calcolatore della distribuzione binomiale per vedere che la probabilità che la moneta esca testa inferiore o uguale a 43 volte è 0,09667 .
Per approssimare la distribuzione binomiale applicando una correzione di continuità alla distribuzione normale, possiamo utilizzare i seguenti passaggi:
Passaggio 1: verificare che n*p e n*(1-p) siano entrambi almeno 5 .
n*p = 100*0,5 = 50
n*(1-p) = 100*(1 – 0,5) = 100*0,5 = 50
Entrambi i numeri sono maggiori o uguali a 5, quindi possiamo continuare.
Passaggio 2: determinare se aggiungere o sottrarre 0,5
Facendo riferimento alla tabella sopra, vediamo che dovremmo aggiungere 0,5 quando lavoriamo con la probabilità sotto forma di X ≤ 43. Quindi, troveremo P(X< 43,5).
Passaggio 3: Trova la media (μ) e la deviazione standard (σ) della distribuzione binomiale.
µ = n*p = 100*0,5 = 50
σ = √ n*p*(1-p) = √ 100*,5*(1-,5) = √ 25 = 5
Passaggio 4: Trova il punteggio z utilizzando la media e la deviazione standard trovate nel passaggio precedente.
z = (x – μ) / σ = (43,5 – 50) / 5 = -6,5 / 5 = -1,3.
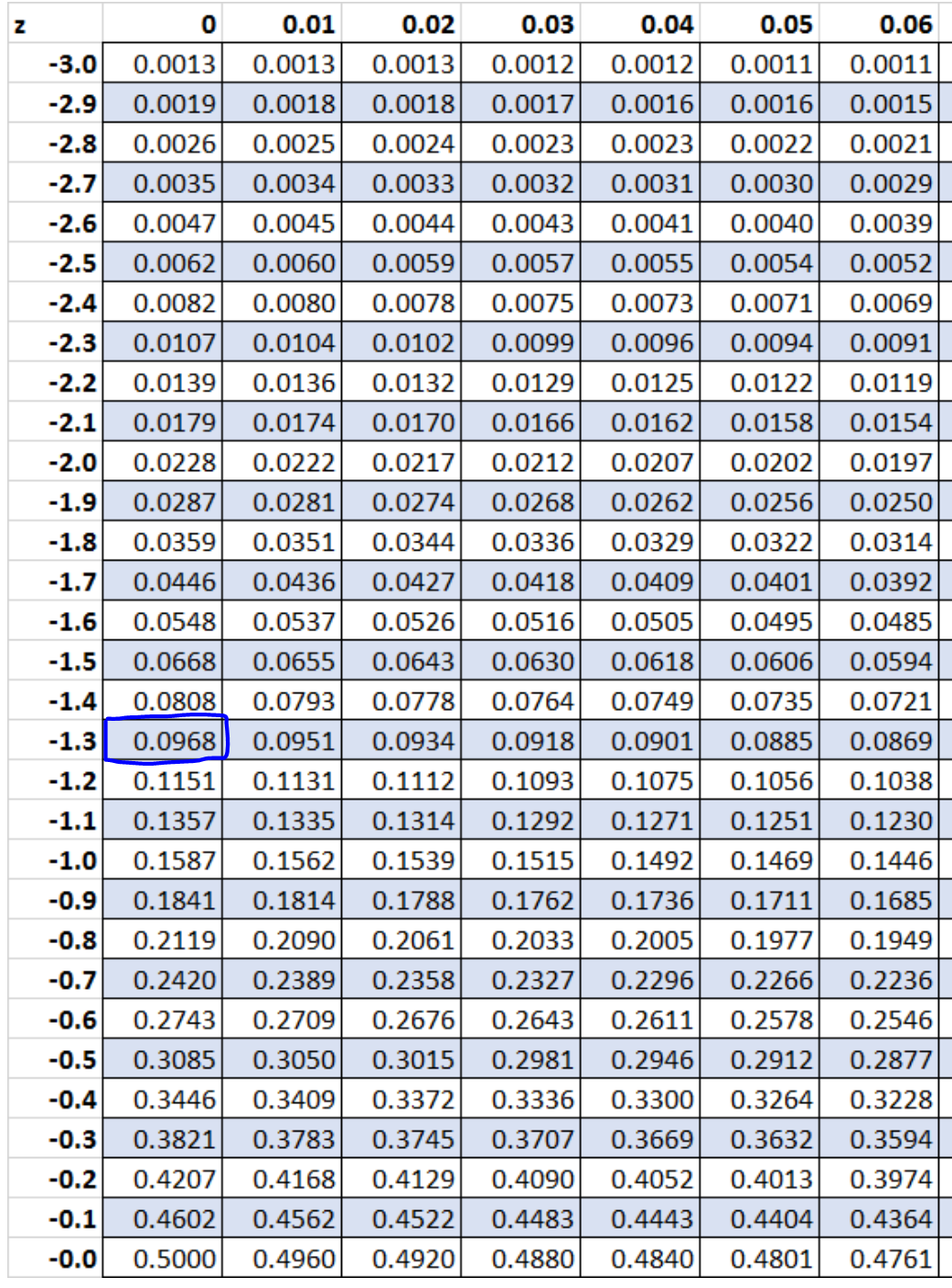
Passaggio 5: utilizzare la tabella Z per trovare la probabilità associata al punteggio z.
Secondo la tabella Z, la probabilità associata a z = -1,3 è 0,0968 .
Quindi la probabilità esatta che abbiamo trovato utilizzando la distribuzione binomiale era 0,09667 mentre la probabilità approssimativa che abbiamo trovato utilizzando la correzione di continuità con la distribuzione normale era 0,0968 . Questi due valori sono abbastanza chiusi.
Quando utilizzare la correzione di continuità
Prima che esistessero i moderni software statistici e i calcoli dovessero essere eseguiti manualmente, le correzioni di continuità venivano spesso utilizzate per trovare probabilità che coinvolgevano distribuzioni discrete. Oggi, le correzioni di continuità svolgono un ruolo minore nel calcolo delle probabilità poiché di solito possiamo fare affidamento su software o calcolatori per calcolare le probabilità per noi.
Si tratta invece semplicemente di un argomento trattato nei corsi di statistica per illustrare la relazione tra una distribuzione binomiale e una distribuzione normale e per mostrare che è possibile per una distribuzione normale approssimare una distribuzione binomiale applicando una correzione di continuità.
Calcolatore per la correzione della continuità
Utilizza il calcolatore della correzione di continuità per applicare automaticamente una correzione di continuità a una distribuzione normale per approssimare le probabilità binomiali.